直角坐标XY和经纬度BL正算反算（西安80坐标3度分带）php

本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qyh666/article/details/80020876
我采用120度径线作为中央子午线，可采用3度带投影。需要用其他坐标可以修改参数$_a, ${}_f,$zoneWide,$longitude0北京54坐标6度分带参数是：$_a = 6378245.0; $_f = 1.0 / 298.3; $zoneWide = 6;

/**
 * XY转经纬度
 */
function XYtoBL($X, $Y)
    {
        $_a = 6378140.0;
        $_f = 1/298.257;
        $zoneWide = 3;//可采用3度带投影
        $PI = 3.14159265353846;
        $iPI = 0.0174532925199433; //3.1415926535898/180.0; 
        $ProjNo = floor($X / 1000000.0); //查找带号
        $longitude0 = 120;//若采用120度径线作为中央子午线
        $longitude0 = $longitude0 * $iPI; //中央经线
        $X0 = $ProjNo * 1000000 + 500000;
        $Y0 = 0;
        $xval = $X - $X0;
        $yval = $Y - $Y0; //带内大地坐标
        $e2 = 2 * $_f - $_f * $_f;
        $e1 = (1.0 - sqrt(1 - $e2)) / (1.0 + sqrt(1 - $e2));
        $ee = $e2 / (1 - $e2);
        $M = $yval;
        $u = $M / ($_a * (1 - $e2 / 4 - 3 * $e2 * $e2 / 64 - 5 * $e2 * $e2 * $e2 / 256));
        $fai = $u + (3 * $e1 / 2 - 27 * $e1 * $e1 * $e1 / 32) * sin(2 * $u) + (21 * $e1 * $e1 / 16 - 55 * $e1 * $e1 * $e1 * $e1 / 32) * sin(4 * $u) + (151 * $e1 * $e1 * $e1 / 96) * sin(6 * $u) + (1097 * $e1 * $e1 * $e1 * $e1 / 512) * sin(8 * $u);
        $C = $ee * cos($fai) * cos($fai);
        $T = tan($fai) * tan($fai);
        $NN = $_a / sqrt(1.0 - $e2 * sin($fai) * sin($fai));
        $R = $_a * (1 - $e2) / sqrt((1 - $e2 * sin($fai) * sin($fai)) * (1 - $e2 * sin($fai) * sin($fai)) * (1 - $e2 * sin($fai) * sin($fai)));
        $D = $xval / $NN;
        //计算经度(Longitude) 纬度(Latitude)
        $longitude1 = $longitude0 + ($D - (1 + 2 * $T + $C) * $D * $D * $D / 6 + (5 - 2 * $C + 28 * $T - 3 * $C * $C + 8 * $ee + 24 * $T * $T) * $D * $D * $D * $D * $D / 120) / cos($fai);
        $latitude1 = $fai - ($NN * tan($fai) / $R) * ($D * $D / 2 - (5 + 3 * $T + 10 * $C - 4 * $C * $C - 9 * $ee) * $D * $D * $D * $D / 24 + (61 + 90 * $T + 298 * $C + 45 * $T * $T - 256 * $ee - 3 * $C * $C) * $D * $D * $D * $D * $D * $D / 720);
        //转换为度 DD
        $longitude = round(($longitude1 / $iPI) * 1000000) / 1000000.0;
        $latitude = round(($latitude1 / $iPI) * 1000000) / 1000000.0;
        return array($longitude, $latitude);
    }

经纬度转XY：

/**
 * 经纬度转XY：
 */    
function BLtoXY($latitude, $longitude)
    {
        $_a = 6378140.0;
        $_f = 1/298.257;
        $zoneWide = 3;
        $PI = 3.14159265353846;
        $iPI = 0.0174532925199433; //3.1415926535898/180.0; 
        //ZoneWide = 6; //6度带宽 
        $ProjNo = floor($longitude / $zoneWide);
        // $longitude0 = $ProjNo * $zoneWide + $zoneWide / 2;
        $longitude0 = 120;//若采用120度径线作为中央子午线
        $longitude0 = $longitude0 * $iPI;
        $latitude0 = 0;
        $longitude1 = $longitude * $iPI; //经度转换为弧度
        $latitude1 = $latitude * $iPI; //纬度转换为弧度
        $e2 = 2 * $_f - $_f * $_f;
        $ee = $e2 * (1.0 - $e2);
        $NN = $_a / sqrt(1.0 - $e2 * sin($latitude1) * sin($latitude1));
        $T = tan($latitude1) * tan($latitude1);
        $C = $ee * cos($latitude1) * cos($latitude1);
        $A = ($longitude1 - $longitude0) * cos($latitude1);
        $M = $_a * ((1 - $e2 / 4 - 3 * $e2 * $e2 / 64 - 5 * $e2 * $e2 * $e2 / 256) * $latitude1 - (3 * $e2 / 8 + 3 * $e2 * $e2 / 32 + 45 * $e2 * $e2 * $e2 / 1024) * sin(2 * $latitude1) + (15 * $e2 * $e2 / 256 + 45 * $e2 * $e2 * $e2 / 1024) * sin(4 * $latitude1) - (35 * $e2 * $e2 * $e2 / 3072) * sin(6 * $latitude1));
        $xval = $NN * ($A + (1 - $T + $C) * $A * $A * $A / 6 + (5 - 18 * $T + $T * $T + 72 * $C - 58 * $ee) * $A * $A * $A * $A * $A / 120);
        $yval = $M + $NN * tan($latitude1) * ($A * $A / 2 + (5 - $T + 9 * $C + 4 * $C * $C) * $A * $A * $A * $A / 24 + (61 - 58 * $T + $T * $T + 600 * $C - 330 * $ee) * $A * $A * $A * $A * $A * $A / 720);
        $X0 = 1000000 * ($ProjNo + 1) + 500000;
        $Y0 = 0;
        $X = round(($xval + $X0) * 100) / 100.0;
        $Y = round(($yval + $Y0) * 100) / 100.0;
        return array($X, $Y);
    }

**下面是概念描述。

转自https://www.cnblogs.com/xieqianli/p/4186281.html
地球坐标系与投影方式的理解(关于北京54,西安80,WGS84;高斯,兰勃特,墨卡托投影)

一、地球模型

地球是一个近似椭球体，测绘时用椭球模型逼近，这个模型叫做参考椭球，如下图：

赤道是一个半径为a的近似圆，任一圈经线是一个半径为b的近似圆。a称为椭球的长轴半径，b称为椭球的短轴半径。

a≈6378.137千米，b≈6356.752千米。（实际上，a也不是恒定的，最长处和最短处相差72米，b的最长处和最短处相差42米，算很小了）

地球参考椭球基本参数：

长轴：a

短轴：b

扁率：α=(a-b) / a

第一偏心率：e=√(a2-b2) / a

第二偏心率：e’=√(a2-b2) / b

这几个参数定了，参考椭球的数学模型就定了。

什么是大地坐标系？

大地坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用大地经度、大地纬度和大地高度表示：(L, B, H)。

空间直角坐标系是以参考椭球中心为原点，以原点到0度经线与赤道交点的射线为x轴，原点到90度经线与赤道交点的射线为y轴，以地球旋转轴向北为z轴：(x, y, z)

共同点：显然，这两种坐标系都必须基于一个参考椭球。

不同点：大地坐标系以面为基准，所以还需要确定一个标准海平面。而空间直角坐标系则以一个点为基准，所以还需要确定一个中心点。

只要确定了椭球基本参数，则大地坐标系和空间直角坐标系就相对确定了，只是两种不同的表达而矣，这两个坐标系的点是一一对应的。

二、北京54，西安80，WGS84

网上的解释大都互相复制，语焉不详，隔靴搔痒，说不清楚本质区别。为什么在同一点三者算出来的经纬度不同？难道只是不认同对方的测量精度吗？为什么WGS84选地球质心作原点，而西安80选地表上的一个点作原点？中国选的大地原点有什么作用？为什么选在泾阳县永乐镇？既然作为原点，为什么经纬度不是0？下面是我个人的理解。

首先，三者采用了不同的参考椭球建立模型，即长短轴扁率这组参数是不同的。

北京54： 长轴6378245m，短轴6356863，扁率1/298.2997381

西安80： 长轴6378140m，短轴6356755，扁率1/298.25722101

WGS84：长轴6378137.000m，短轴6356752.314，扁率1/298.257223563，第一偏心率0.081819790992，第二偏心率0.082095040121

这些参数不同，决定了椭球模型的几何中心是不同的。那么为什么这三种坐标系的参数有这么大差别呢？除了测量精度不同之外，还有一个原因，就是侧重点不一样。

WGS84是面向全球的，所以它尽量逼近整个地球表面，优点是范围大，缺点是局部不够精确。

北京54用的是前苏联的参数，它是面向苏联的，所以它在前苏联区域这个曲面尽量逼近，而其它国家地区偏多少它不管。它以苏联的普尔科沃为中心，离那越远，误差就越大。

西安80是面向中国的，所以它在中国区域这个曲面尽量逼近，而其它国家地区偏多少它不管。而且这个逼近是以西安附近的大地原点为中心的，也就是说，在西安大地原点处，模型和真实地表参考海平面重合，误差为0，而离大地原点越远的地方，误差越大。所谓的大地原点就是这么来的，它是人为去定的，而不是必须在那里，它要尽量放在中国的中间，使得总的误差尽量小而分布均匀。然后，我国在自已境内进行的建筑，测绘，勘探什么的所绘制的图，都以这个大地原点为基准，去建立各种用途的地表坐标系，就能统一起来了。

所以在中国区域，WGS84模型是没有西安80模型那么准确。而用西安80模型来算美国的点，则更不准确。现在更新为2000国家大地坐标系，参数比西安80更精确了，而道理是一样的。

都说WGS84是质心坐标系，北京54，西安80是参心坐标系，何谓质心？何谓参心？

质心好理解，就是地球体的质量中心，WGS84坐标系面向全球定位，所以它所建立的模型是最中庸的，没有偏向任何一个地区，椭球体模型的几何中心与地球质心重合时，模型就会最接近整个地球。

而北京54和西安80侧重于局部的精确性，而舍弃整体的精确性，当椭球模型(西安80)在中国区域最精确时，它的几何中心肯定不是地球质心，而在别的地方。所以这个几何中心称之为参考中心，简称参心。

地球上一个点经纬度，是基于参考椭球来算的，所以，同一个地方，用北京54，西安80，WGS84算出来的经纬度是三个不一样的值。由于GPS用的是WGS84，所以我们手机看到的是WGS84坐标系的经纬度。

三、地图在平面上的投影

我们的地图，总得画在纸上，在显示器上吧，不然到处拎着地球仪？地球上的点是用经纬度表示的，纬度越高的地方，1度的经度的距离就越短。那么，问题来了，地球表面是曲面，而且经纬度与长度距离并不是简单的比例关系，怎样画到平面上？答案是，投影算法。好，问题又来了，投影算法哪家强？

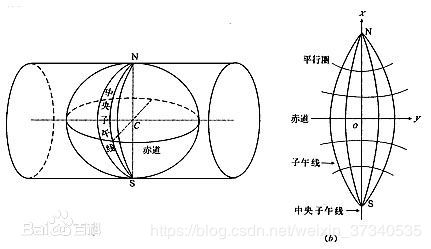
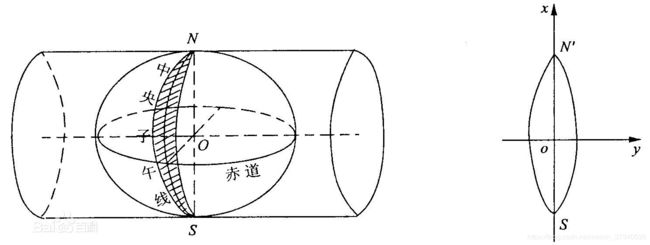
1.高斯-克吕格投影

假设一个椭圆柱面与地球椭球体面横切于某一条经线上，按照等角条件将中央经线东、西各3°或1.5°经线范围内的经纬线投影到椭圆柱面上，然后将椭圆柱面展开成平面而成的。

高斯克吕格投影是分带投影的，主要分有3度带和6度带两种。3度带就是经度每3度一个带，全球切成120个带；6度带就是经度每6度一个带，全球切成60个带。不同的带之间各有各的原点自成xy坐标系，不能用本带的xy坐标系去计算其它带的，因为原点都不同了。
高斯克吕格投影的变形分析：
①中央经线上无变形，满足投影后长度比不变的条件；
②除中央经线上长度比为1以外，其它任何点长度比均大于1；
③在同一条纬线上，离中央经线越远则变形越大，最大值位于投影带边缘。
④在同一条经线上，纬度越低变形越大，最大值位于赤道上。
⑤等角投影，无角度变形，面积比为长度比的平方。
⑥长度比的等变形线平行于中央轴子午线。

优点：长度和面积变形是最小的(比起其它投影)。
缺点：需要分带，相邻的带不能拼接(上尖下宽怎么接？好难个)，导致覆盖范围小。
所以高斯投影适用于小地区的地图，一个带就能覆盖的地区。

2.兰勃特投影

有两种：
①等角圆锥投影。

设想用一个正圆锥切于或割于球面，应用等角条件将地球面投影到圆锥面上，然后沿一母线展开成平面。投影后纬线为同心圆圆弧，经线为同心圆半径。没有角度变形，经线长度比和纬线长度比相等。适于制作沿纬线分布的中纬度地区中、小比例尺地图。市面上的中国地图应该就是用这种投影的。

②等积方位投影。

设想球面与平面切于一点，按等积条件将经纬线投影于平面而成。按投影面与地球面的相对位置，分为正轴、横轴和斜轴3种。在正轴投影中，纬线为同心圆，其间隔由投影中心向外逐渐缩小，经线为同心圆半径。在横轴投影中，中央经线和赤道为相互垂直的直线，其他经线和纬线分别为对称于中央经线和赤道的曲线。在斜轴投影中，中央经线为直线，其他经线为对称于中央经线的曲线。该投影无面积变形，角度和长度变形由投影中心向周围增大。横轴投影和斜轴投影较常应用，东西半球图和分洲图多用此投影。

3.墨卡托投影

假设地球被围在一中空的圆柱里，其基准纬线与圆柱相切（赤道）接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定基准纬线上的“墨卡托投影”绘制出的地图。
优点：没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角。
缺点：长度和面积变形明显，纬线间隔从基准纬线处向两极逐渐增大。但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。
墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。
谷歌地图，百度地图用的就是墨卡托投影，且以赤道作基准纬线。