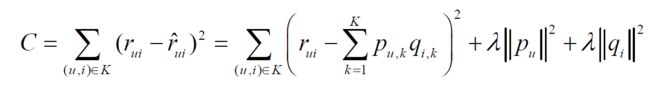关于矩阵分解：特征值分解 svd分解 mf分解 lmf分解 pca 以及个性化推荐 fm ffm als

矩阵分解作用很多：矩阵填充（通过矩阵分解来填充原有矩阵，如als 就是填充原有矩阵），清理异常值与离群点，降维，压缩，个性化推荐，间接的特征组合（计算特征件相似度）

——————————————————————————————————————————

矩阵分解方法：

特征值分解：分解为一个特征向量矩阵 与  特征值（对角矩阵）

————————————

svd分解（奇异值分解）：

X=USV⊤

对角阵 S对角线上的元素是奇异值， U和 V是正交矩阵

mn矩阵分解为：[m*k] [k*k][k*n]矩阵，关于svd分解的基础：http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html  这篇文章不错

————————————

mf分解（matrix factorization model）：mn矩阵分解为：[m*k][k*n]矩阵，由他逐渐演化出LFM 隐语义分解（其中第一个矩阵代表用户矩阵，第二个矩阵代表商品矩阵，k代表用户 or 商品的隐式特征。）Rm×n≈Pm×k×Qk×n=R^m×n

mf分为很多种：

基本矩阵分解（basic MF）

正则化矩阵分解（Regularized MF）

基于概率的矩阵分解（PMF）

非负矩阵（Non-negative MF）

正交非负矩阵（Orthogonal non-negative MF）

——————————————————————————————————————————

矩阵分解的作用：降维，压缩

pca分解：降维，压缩，

先说PCA吧，PCA降维的大致思想就是：挑选特征明显的、显得比较重要的信息保留下来。

那么关键就是【特征明显的，重要的信息】如何选择？ 选择标准有两个：
1： 同一个维度内的数据，方差大的比较明显，因为方差大表示自己和平均水平差异大，有个性，降维后也最可能分的开～
2： 两个不同维度间关联度越小越好，因为关联度小表示这两个维度表征共同信息的量比较少，最理想就是两个维度不相关，相关度为0（相关度可以用协方差cov(a,b)表示），在线性空间内表现为两个维度正交～

作者：henryWang
链接：https://www.zhihu.com/question/38319536/answer/131150925
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

pca 与 svd的关系： pca是一种手段，svd是pca求解的方法，svd处理非方阵，当然我们可以通过特征值分解来做pca

详情请查看：http://blog.csdn.net/wangjian1204/article/details/50642732

下面说一下为啥还有SVD，上面我们说PCA针对的是协方差矩阵C，但你得知道协方差矩阵是个方阵啊，难道不是方阵我们就不资瓷么？？ 所以就有了SVD～～

大概可以把SVD看作是对非方阵做PCA处理的一种方式啦，毕竟两者的套路都差不多，分解出特征值（SVD里是奇异值，数据XX‘的特征值的平方根），挑比较大的特征值对应的特征向量构成投影矩阵，然后做线性变换（将数据X投影到低维空间）

作者：henryWang
链接：https://www.zhihu.com/question/38319536/answer/131150925
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

——————————————————————————————————————————

矩阵分解的作用：矩阵填充—通过矩阵分解实现

1，传统的矩阵填充方式：填充矩阵R

A，在矩阵分解之前需要先把矩阵R缺失值补全（定义随机值），补全之后稀疏矩阵R表示成稠密矩阵R'，

B，然后将R’分解成如下形式：

R' = U^TSV

C，然后再选取U中的K列和V中的S行作为隐特征的个数，达到降维的目的。K的选取通常用启发式策略。

这种方法有两个缺点：

第一是补全成稠密矩阵之后需要耗费巨大的存储空间，在实际中，用户对物品的行为信息何止千万，对这样的稠密矩阵的存储是不现实的；

第二，SVD的计算复杂度很高，更不用说这样的大规模稠密矩阵了。所以关于SVD的研究很多都是在小数据集上进行的。

第三，这种填充方式本身存在问题。 其一，填充大大增加了数据量，增加了算法复杂度。其二，简单粗暴的数据填充很容易造成数据失真

我们都知道，现实生活中的User-Item矩阵极大(User数量极大、Item数量极大)，而用户的兴趣和消费能力有限，对单个用户来说消费的物品，产生评分记录的物品是极少的。这样造成了User-Item矩阵含有大量的空值，数据极为稀疏。矩阵分解的核心思想认为用户的兴趣只受少数几个因素的影响—低秩，因此将稀疏且高维的User-Item评分矩阵分解为两个低维矩阵——降维，即通过User、Item评分信息来学习到的用户特征矩阵P和物品特征矩阵Q，通过重构的低维矩阵预测用户对产品的评分。由于用户和物品的特征向量维度比较低，因而可以通过梯度下降(Gradient Descend)的方法高效地求解，分解示意图如下所示。

　　如上所述，User-Item评分矩阵维度较高且极为稀疏，传统的奇异值分解方法只能对稠密矩阵进行分解，即不允许所分解矩阵有空值。因而，若采用奇异值分解，需要首先填充User-Item评分矩阵，显然，这样造成了两个问题。

• 其一，填充大大增加了数据量，增加了算法复杂度。
• 其二，简单粗暴的数据填充很容易造成数据失真。

　　这些问题导致了传统的SVD矩阵分解表现并不理想。之后，Simon Funk在博客上公开发表了一个只考虑已有评分记录的矩阵分解方法，称为Funk-SVD，也就是被Yehuda Koren称为隐语义模型的矩阵分解方法—增加隐向量。他简单地认为，既然我们的评价指标是均方根误差(Root Mean Squared Error, RMSE)，那么可以直接通过训练集中的观察值利用最小化RMSE学习用户特征矩阵P和物品特征Q，并用通过一个正则化项来避免过拟合。

2，隐语义（LFM）矩阵填充方式：填充矩阵R

将评分矩阵R分解为用户矩阵U和项目矩阵S， 最初随机填充初始值，之后梯度下降求解最优值，获得最终结果，通过不断的迭代训练使得U和S的乘积越来越接近真实矩阵，矩阵分解过程如图：

隐语义矩阵分解：A = XY^{T，X叫做用户因子矩阵，Y叫做物品因子矩阵，}

通常上式不能达到精确相等的程度，我们要做的就是要最小化他们之间的差距，从而又变成了一个最优化问题。求解最优化问题我们很容易就想到了随机梯度下降，其中有一种方法就是这样，通过优化如下损失函数来找到X和Y中合适的参数：

具体请查看：

http://blog.csdn.net/shuaishuai3409/article/details/50821071

http://www.cnblogs.com/mooba/p/6539142.html

——————————————————————————————————————————

隐向量矩阵分解（填充）在隐语义模型（协同过滤）中的应用：（无明确特征输入，r为隐式特征，用户自定义r值，对于训练集外数据无法预测）

在推荐系统里，如果有评分矩阵M，其中的每个元素(i, j)可存在可缺失，存在时代表用户i对商品j的评分，那么当我们基于协同过滤来推荐时，这个推荐问题可以较好地归约到矩阵填充这个task上来。这是因为协同过滤本质上是考虑大量用户的偏好信息（协同），来对某一用户的偏好做出预测（过滤），那么当我们把这样的偏好用评分矩阵M表达后，这即等价于用M其他行的已知值（每一行包含一个用户对所有商品的已知评分），来估计并填充某一行的缺失值。若要对所有用户进行预测，便是填充整个矩阵，这是所谓“协同过滤本质是矩阵填充”。

那么，这里的矩阵填充如何来做呢？矩阵分解是一种主流方法。这是因为，协同过滤有一个隐含的重要假设，可简单表述为：如果用户A和用户B同时偏好商品X，那么用户A和用户B对其他商品的偏好性有更大的几率相似。这个假设反映在矩阵M上即是矩阵的低秩。极端情况之一是若所有用户对不同商品的偏好保持一致，那么填充完的M每行应两两相等，即秩为1。所以这时我们可以对矩阵M进行低秩矩阵分解，用U*V来逼近M，以用于填充——对于用户数为m，商品数为n的情况，M是m*n的矩阵，U是m*r，V是r*n，其中r是人工指定的参数。这里利用M的低秩性，以秩为r的矩阵M'=U*V来近似M，用M'上的元素值来填充M上的缺失值，达到预测效果。

（转载自：

作者：知乎用户
链接：https://www.zhihu.com/question/47442596/answer/106030329
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
）

svd协同过滤：非隐语义语义（需要矩阵填充）+ 显式反馈（rating值为用户输入）

svd++协同过滤：非隐语义语义（需要矩阵填充）+ 隐式反馈（rating值为点击、购买等用户操作）

svd-funk：隐语义矩阵分解

ALS：使用MF正则分解为用户矩阵、商品矩阵，采用交替最小二乘法 求解
详细请查看http://blog.csdn.net/oucpowerman/article/details/49847979

详细请查看：

http://blog.csdn.net/winone361/article/details/49491709 svd pmf svd++

http://blog.csdn.net/winone361/article/details/49427627 svd++

——————————————————————————————————————————

隐语义矩阵分解（填充）在直接推荐、广告系统中ctr、cvr预估中的应用：（有明确的大量特征输入—所以存在数据稀疏问题，对于训练集外数据均可预测）

FM 与 FFM：FM 解决了量大问题：矩阵稀疏问题、特征之间关系（由于特征很多为0 or null，所以也通过隐向量方式解决特征之间关系的矩阵稀疏问题）问题：

矩阵稀疏问题解决方式：隐向量矩阵分解

特征之间关系问题：向量间距离计算—内积计算特征之间的余弦距离，来完成特征间关系的计算 + 隐向量的矩阵分解

详情请查看：

http://m.blog.csdn.net/zhangf666/article/details/75071195

http://blog.csdn.net/u013818406/article/details/70194575

特征值分解、SVD、MF、SVD++ 、FM、ALS 均完成了矩阵分解操作，区别在于SVD与 SVD++均需要矩阵填充， 而 funk-svd 与FM、 ALS 均采用MF分解模式，进行隐语义分解，其中ALS主要用于协同过滤，而FM主要用于ctr cvr预估，FM又解决了了特征关系问题—通过向量内积。