Graph Neural Networks (GNN)（一）：Spatial-GNN

1. 想法

CNN 中的卷积核（e.g., 3 * 3）算某一个像素点的 feature 的时候，可以看成把这个像素点周围的像素点的特征按照一定的权重加权求和。

卷积操作类似于内积，即把卷积核里的每个权重和对应像素点值相乘，最后相加，得到的结果就是这个点的新的特征。

Spatial-GNN 想要把这种卷积操作直接推广到 Graph 上。

2. 做法

将某个节点周围的领域节点特征收集起来，进行某一种操作，然后更新这个节点的特征。
图片来源：李宏毅老师 2020 课程：

上面我觉得直接把 i 看成 0 来理解会好一些，假设第 0 层的图和特征如上面图左边所示。

为了更新 $h_3^0$ （也就是第 0 层的 3 号节点）的节点特征，那么类似的我们需要将它周围的节点的特征聚合（aggregate）起来，然后进行某种操作，来更新这个节点的特征。类似于卷积中除了对周围像素操作职位，也对自己本身做了操作，因此 Spatial-GNN 通常也会结合自己本身的特征来更新下一次的特征。

这里在我读过的论文里面总结得最好的论文是 GIN《HOW POWERFUL ARE GRAPH NEURAL NETWORKS?》

$a_v^{(k)}=$ AGGREGATE ${}^{(k)}\left(\left\{h_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right),h_v^{(k)}={\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{B}\mathrm{I}\mathrm{N}\mathrm{E}}^{(k)}\left(h_v^{(k-1)},a_v^{(k)}\right)$

$k$ 代表第 k 层网络，经过 $k$ 层网络的某一节点会收集到他 $k$ 跳邻居的节点信息。
AGGREGATE 操作就是讲收集到的节点的特征进行聚合，聚合方案的不同是导致这一类方法不同模型的主要原因。同样的 COMBINE 操作就是讲聚合的特征和自己节点这一层的特征结合起来，形成新的特征。这样就可以经过 $k$ 层网络之后，每个节点就会根据自己周围的拓扑结构和特征，得到新的特征，可以更好的用于下游任务。

当然对于图分类的任务，需要整个图的特征：

$h_G=\mathrm{READOUT}\left(\left\{h_v^{(K)}|v\in G\right\}\right)$

其中 $K$ 是最后一层的网络，这里表示将最后一层所有节点的特征进行某种 READOUT 操作，就得到整个图的特征。当然也可以把前面所有层的特征一起进行操作，甚至加权都是可以的。比如 GIN 中就用到了所有层的特征。

3. 经典例子：

接下来就是这一类方法的经典例子：这里面有大名鼎鼎的 GAT 和 GraphSage。

3.1 NN4G

论文《Neural Network for Graphs: A Contextual Constructive Approach》

NN4G 的想法很简单：就是把一跳邻居的节点特征相加，然后通过一个权重矩阵做变换，加上自身的值做一个权重矩阵相乘的变换。这里的 $x_3$ 是这个节点本来值（比如化学分子中的原子符号），然后经过一种 embedding（例如 word2vec 等），得到第一次的特征 $h_3^0$。通常现有的数据集预处理原始数据的过程是已经实现了的，因此，我们可以认为他 COMBINE 的就是上次层自己的特征。

对于获取整个图的特征：

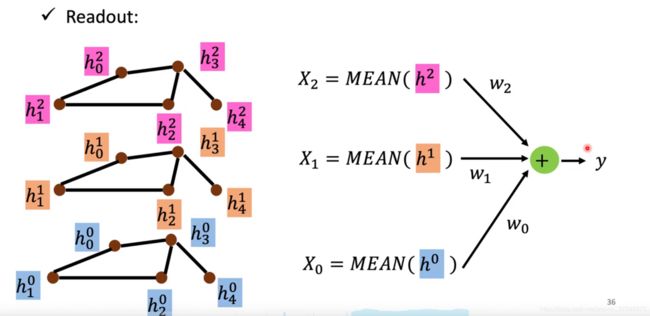
将每一层的所有节点特征求平均得到这一层的图表示，然后将所有层的图片是加权求和得到最终的图表示。

1. AGGREGATE：求和之后做一个 Transform
2. COMBINE：加上自身做一个 Transform 的结果。
3. READOUT：先用平均操作求每一层的图表示，然后将所有层的图表示加权求和得到最终的图表示。

3.2 DCNN

论文：《Diffusion-Convolutional Neural Networks》

$\mathrm{MEAN}(d(3,\cdot )=1)$ 指的是在 Graph 中距离某个节点距离为 1 的节点。
$\mathrm{MEAN}(d(3,\cdot )=2)$ 指的是在 Graph 中距离某个节点距离为 2 的节点。
这样就很好理解 diffusion 扩散操作的含义了。

这样第一层就收集 1 跳邻居的信息，第二层就收集 2 跳邻居的信息。

这里收集多跳邻居的行为和其他大部分方法有点差异：大部分方法并不是显式的收集多跳邻居，而是按照下面方法：第一层网络每个节点收集自己 1 跳邻居的信息更新节点特征。第二层也是收集自己 1 跳邻居的信息更新节点特征。注意，这种行为是可以收集到 2 跳邻居的信息的，因为第二层自己 1 跳邻居已经在第一层收集了他们的 1 跳邻居，而 1 跳邻居的 1 跳邻居中包含了自己的 2 跳邻居。
当然这种显式的方法本质上是一样的，只是最终学到的网络参数而已

进一步，将每一层网络中所有节点的向量组成一个矩阵：

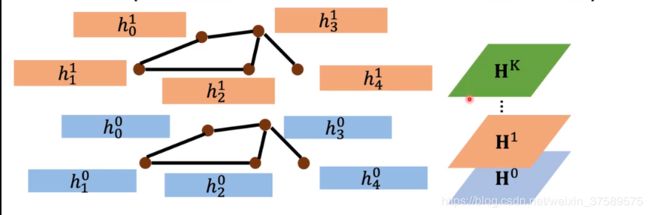
${\mathbf{H}}^{\mathbf{K}}$ 代表第 $K$ 层的矩阵，假设有 $n$ 个节点，特征维度为 $d$，那么这个矩阵就是一个 $n\times d$ 的矩阵，然后 $K$ 层，就有一个 $K\times n\times d$ 的一个张量。

然后最后的特征不是简单的最后一层网络输出的节点特征，他显式的考虑之前的节点。

图中所示的意思是，将 $n\times d$ 矩阵中的某一行拿出来，也就是某一节点的特征，然后 $K\times n\times d$ 张量就成了一个 $K\times d$ 的矩阵，然后做一个 Transform （乘以一个矩阵），最后得到这个节点的特征向量。

其实我们可以这样想节点最后特征的形成：

1. 第 $K$ 层使用 $K$ 跳邻居的信息求平均得到第 $K$ 层的节点特征。
2. 将所有层的节点特征构成一个矩阵，然后做一个 Transform （乘以一个矩阵），最后得到这个节点最终的特征向量。

之所以连接成矩阵形式，是为了充分利用 GPU 并行计算的能力。
因此这里的 AGGREGATE 方案和 COMBINE 方案有一点差异：

1. AGGREGATE：求平均。但是并不是简单的拿最后一层特征作为输出特征，而是把所有层特征做一个 Transform 得到最后的节点特征。
2. COMBINE：没有加上自身。
3. READOUT：简单的把所有节点表示做平均。但是文中也提到在这个方案里面做平均效果不太好。

3.3 MoNet

论文《Geometric deep learning on graphs and manifolds using mixture model CNNs》

MoNet 也提出了一个统一的框架，并且表示 GCN 等都是这个框架的特例。其实 GCN 也可以看成一种 Spatial-GNN，即使它是从频谱 GNN 推导出来的。
MoNet 的基本公式如下：


其中 $\mathcal{N}(x)$ 代表 $x$ 的邻居节点， $\mathbf{u}(x,y)$ 是一种定义好的节点之间的度量（我们可以理解为距离、相似度等），注意这个度量是一个向量，然后我们通过一个网络/加权函数（也可以看作核），这个网络可以理解为一种模式（然后检查这个节点和邻居节点组合一起有没有构成某种模式，也就是模式匹配），然后可以有多个这样的网络（核或者模式），最后所有邻居节点和所有模式加权求和，更新这个节点的特征。

不同的度量选择和不同的加权函数选择对应不同的方法：

MoNet 使用的核是多个高斯核，度量是基于节点度的度量，因此也可以认为 MoNet 是一种高斯混合模型（GMM）：

我们可以简单的理解，$\mathbf{u}(x,y)$ 和 $w_j(\mathbf{u})$ (多个 $w_j(\mathbf{u})$) 一起计算这个邻居节点对于这个本身节点的重要性，然后所有邻居节点加权求和来更新这个节点的特征。

这个时候一个自然地问题，我们上面表中的方法和 Monet 中的 $\mathbf{u}(x,y)$ 和 $w_j(\mathbf{u})$ 都是手动定义的， 因此一个自然地想法，这个重要性（权重）我们自己去学，这也就是后面 GAT 的想法。

1. AGGREGATE：求加权和。权值的计算是通过度量和模式匹配来进行的。
2. COMBINE：可以认为没有加自身的特征，但是在考虑度量和模式的时候都有用到自身的特征。

3.4 GraphSAGE

论文《Inductive Representation Learning on Large Graphs》

半监督学习可以分为：Transductive 和 Inductive

• Transductive（转换的）：测试样本在训练的时候是已知的可用的（当然标签是不知道的，但是我们知道他们的特征）。例如半监督的 Node Classification 中，我们训练的时候用到了测试节点的特征，因为你在聚合周围节点特征的时候，某个训练节点的周围可能是测试节点。
• Inductive（归纳的）：测试样本在训练的时候是不可知不可用的。

大多数现有方法 Graph Embedding 的方法都是 Transductive 的，训练的时候需要所有的节点，无法很好地泛化到之前没有见过的节点。

GraphSAGE：学习一个 function 来通过采样和聚合一个节点领域的特征来生成 Embedding。实际上 GraphSAGE 学习的是一组聚合函数（Aggregate Function），然后在测试的时候使用学习到的这一组聚合函数对节点的领域进行采样和聚合最后得到节点的 embedding。

这是前向算法，也就是假设我们训练好了聚合函数如何在测试的时候使用：这里有 $K$ 个聚合函数，没个函数有自己的权重矩阵 ${\mathbf{W}}^k$。我们可以看成 $K$ 层网络。

我们每次采样都是采样自己的 1 跳邻居，那么是怎么可以收集到多跳邻居的信息的呢？注意，每一次外层循环，我们要对所有节点的特征进行更新，这样我们第 2 层的网络即时采样自己的 1 跳邻居也可以收集到 2 跳邻居的信息，因为在第 1 层网络的时候，1 跳邻居根据自己的 1 跳邻居更新自己的特征（其中包括了 2 跳邻居）。因此 $K$ 个聚合函数，相当于 $K$ 层网络，相当于最终节点会收集到 $K$ 跳邻居的信息。

然后每一次外层循环，都是聚合自己领域节点的信息，然后和本身链接起来，最后更新自身的节点信息。最后一层，也就是第 $K$ 层的输出就是最终的 Embedding。

根据算法，可以发现 GraphSAGE 就是我们 Spatial-GNN 的标准范式

接下来就是具体的聚合方案：

1. Mean aggregator：很好理解，就是对所有领域节点的特征向量求平均，然后和自身向量一起做一个线性变化加一个非线性激活。这种方式做一点细微的修改就和 GCN 很类似了：
   
   这个公式和标准的 GCN 只差一个归一化常数。GCN 可以看成就是把邻居向量和自身向量一起求平均，通过一个线性转换加一个非线性激活，得到新的特征表示，注意这一公式包括了算法中的第 4 行和第 5 行。虽然过程有点差异，但是本质上是类似的，GraphSAGE-Mean 中把自身一起求平均修改为领域节点求平均然后和自身连接在一起。

2. Pooling aggregator：将领域节点向量送到一个完全连接层，然后对输出之后的向量赤化。例如 max-pooling 就是逐元素求最大值。
   

3. LSTM aggregator：我们上面所有的聚合方案都有两个很好地特性：（1）对于不同数量的领域节点，都可以直接使用，避免了 Graph 数据不同节点的领域数不同的问题。（2）与领域节点的输入顺序无关。 但是 LTSM 不一样，LSTM 对输入顺序是很敏感的，但是 LTSM 模型的表现力更强，为了借助这个表现了，GraphSAGE-LSTM 把采样到的节点顺序打乱之后送入 LSTM，得到聚合的向量，然后和自身连接起来，送到一个完全连接层。

模型的训练分为有监督的和无监督的：有监督的很简单，就是根据监督任务定义损失函数，学习每个聚合函数也就是每层网络的参数（聚合方案一旦确定就是不变的）。如果是无监督的，损失函数基于 graph 结构：相邻节点具有相似的特征向量，相互远离的特征向量不同：

${\mathbf{z}}_u^{\top }{\mathbf{z}}_v$ 代表两个节点向量内积，向量相似，内积大，然后取相反数，就是损失函数越小越好。（${\mathbf{z}}_v$ 是在一定长度的随机游走上出现了点，即相近的点，我们期望他们向量相似）。后面的是负采样，$Q\cdot {\mathbb{E}}_{v_n\sim P_n(v)}\log \left(\sigma \left(-{\mathbf{z}}_u^{\top }{\mathbf{z}}_{v_n}\right)\right)$ ，$Q$ 是负采样节点数，负采样中向量内积多了一个相反数，也就是希望负采样向量和这个节点向量差异越大越好。

实验实施：

只需要两个聚合函数，也就是两层网络，第一层采样 25 个邻居节点，第二层采样 10。之所以设置固定的领域节点数，而不是采样所有节点是为了使每个节点的时间空间消耗一直，直接原因就是为了方便简单。至于有的节点少于需要的节点数，那么就是又放回的采样，如果充足的领域节点，那么可以无放回的采样。

优点：（1）可以使用在不断扩张演进的图上；（2）可以泛化到新的图上；

3.5 GAT

论文：《Graph Attention Networks》

GAT 的核心思想就是隐式地给不同领域节点不同的权重，不用像 MoNet 一样手动的定义节点之间的度量，而是通过学习得到的。 GAT 也可用于 Inductive 的半监督学习。

知道想法就是学习加权和的权重，那么就很好理解了：

1. 首先是将节点向量做一个线性变换：$\mathbf{W}\in {\mathbb{R}}^{F^{\prime }\times F}$，然后将两个节点（GAT 中很显然我们只需要聚合领域节点的，因此只需要给每个节点的每个领域节点求 attention）：$e_{ij}=a\left(\mathbf{W}{h}_i,\mathbf{W}{h}_j\right)$，其中 ${\mathbb{R}}^{F^{\prime }}\times {\mathbb{R}}^{F^{\prime }}\to \mathbb{R}$，表示这个 $e_{ij}$ 是一个实数，来表示这个邻居节点对这个节点的重要性指数。当然一个节点一般具有多个邻居节点，因此对所有邻居节点的重要性指数，softmax 归一化：
   
   当然在实际操作中，加入了一个 LeakyReLU 的非线性激活：
   
   其中 $\mathrm{a}\in {\mathbb{R}}^{2F^{\prime }}$ 将连接的两个向量转换为一个实数。
2. 然后每个节点的特征，就是算到的 attention 作为权重的加权和：
   
3. 文中提到为了稳定自注意力机制的训练稳定性，使用了多头注意力机制，其实就是上面的过程用多个不同参数相同结构的网络重复使用，然后将所有网络的输出连接起来（最后一层去平均）：
   
   
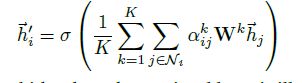
   优点：（1）权重自己学的，比自己定义的权重计算方法好，提高了模型的表现力；学到的权重可以用来解释一些现象，提高可解释性。（2）时间复杂度不高：$O\left(|V|F{F}^{\prime }+|E|F^{\prime }\right)$；（3）

3.6 GIN

论文《How Powerful are Graph Neural Network?》
文章主要贡献：

1. 证明了GNN最多只和 Weisfeiler-Lehman (WL) test 一样有效，即WL test 是GNN性能的上限
2. 提供了如何构建GNN，使得和WL一样有效
3. 用该框架分析了GCN和GraphSAGE等主流GNNs在捕获图结构上的不足和特性
4. 建立了一个简单的神经结构——图同构网络(GIN)，并证明了它的判别/表达能力和WL测试一样

文中提出的框架首先将给定节点的邻居的特征向量集表示为一个多集，即，一个可能有重复元素的集合。然后，可以将 GNN 中的邻居聚合看作是多集上的聚合函数。因此，为了拥有强大的表示能力，GNN 必须能够将不同的多集聚合到不同的表示中。单射函数指的是：对每一值域内的 y，存在至多一个定义域内的 x 使得 f(x) = y。也就是当且仅当 a = b, f(a) = f(b)，在 GNN 中 也就是具有完全相同的领域的一个节点才会被映射为同一个 embedding。

WL 测试和 Spatial-GNN 的联系：Weisfeler-Lehman 迭代进行以下操作得到节点新标签以判断同构性：

1. 聚合方案：聚合每个节点邻域和自身标签。
2. 更新节点标签：使用Hash映射节点聚合标签，作为节点新标签。

文中给出了具体证明（详细证明参考论文）：WL 测试是 GNN 性能的上限。

那么问题来了，什么样的 GNN 和 WL 测试一样强大呢？

如果邻居Aggregate函数和Readout函数是单射的，那么得到的GNN与WL测试一样强大。

$h_v^{(k)}={\mathrm{MLP}}^{(k)}\left(\left(1+{ϵ}^{(k)}\right)\cdot h_v^{(k-1)}+{\sum }_{u\in \mathcal{N}(v)}{h}_u^{(k-1)}\right)$
$h_G=$ CONCAT $\left(\text{ READOUT }\left(\left\{h_v^{(k)}|v\in G\right\}\right)|k=0,1,\dots ,K\right)$
实际上 READOUT 是用的求和，即
$h_G=\mathrm{C}\mathrm{O}\mathrm{N}\mathrm{C}\mathrm{A}\mathrm{T}\left(\mathrm{sum}\left(\left\{h_v^{(k)}|v\in G\right\}\right)|k=0,1,\dots ,K\right)$
最后获取图表示，是将每一层的节点表示 READOUT 然后连接起来。和之前一些方法只操作最后一层不同。

文章实例说明为什么 mean 和 max 的不是最强大的 GNN：

1. （a）中两个图是不同的结构（多集）：但是 Mean 和 Max 都认为是一样的结构。对于 mean: (a + a ) / 2 = (a + a + a) / 3。对于 max: max(a, a) = a = max (a, a, a)。
2. （b） max 方法认为是一样的结构，失效
3. （c）Mean 和 Max 都认为是一样的结构，失效。

由于 mean 和 max-pooling 函数不满足单射性，无法区分某些结构的图，因此不是最强力的 GNN。但是实际中那么多网络使用这两种方法，为什么有效呢？

1. sum：学习全部的标签以及数量，可以学习精确的结构信息
2. mean：偏向学习分布信息。（学习多集中元素的比例，因为按相同倍数扩大，Mean 映射为同一个结果），因此对于分布信息重要的任务，mean 是有效的。并且如果多集中几乎没有重复元素，那么 mean 和 sum 的能力会差不多。
3. max：学习多集的基础集（多集中删除重复元素形成的集合，即形成各不相同的元素集合）。将多集视为普通集合，因为多个相同元素 max 之后就只有这一个元素：max(a, a, b, b, b) = max(a, b)。