通过一个小例子帮助你理解正则化(附python代码）

一.L1和L2正则化简单介绍：

1.L1和L2正则化的作用（这一部分摘自网络，我主要是提供后面的代码说明）：

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择，一定程度上，L1也可以防止过拟合。

L2正则化可以防止模型过拟合(overfitting)

L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚，倾向于更加分散的权重向量。由于输入和权重之间的乘法操作，这样就有一个优良的特性：使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征。L2惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度，这样做可以提高模型的范化能力，降低过拟合的风险。
（转自https://www.cnblogs.com/zhibei/p/12397975.html）

二.代码实现

本例通过两个点拟合出y=ax^2+bx+c曲线，a、b、c为参数，需要我们解出来，当然，会有无数个a、b、c的值满足要求，这就好比深度学习中参数远远多于样本数。正则化可以使得参数的值尽可能接近0。
p1=（x1,y1),p2= (x2,y2)为两个样本点，本例取 p1 = [5, 3],p2= [-3, -9]

1.没有用正则化的例子

损失函数为 $L=[a(X1{)}^2+b(x1)+c-y1{]}^2+[a(X2{)}^2+b(x2)+c-y2{]}^2$

下面展示具体代码:

def No_rugularization(e,f):
    '''
    没有用正则化 abc系数都很大
    :param e: e f为传入的两个点，列表形式如[2,4]
    :param f: 同上
    :return: a,b,c。即一元二次方程的三个系数
    '''
    x1=e[0]
    y1=e[1]
    x2=f[0]
    y2=f[1]
    a=-1000000
    c,b=1000 ,1000
    L=(a*x1**2+b*x1+c-y1)**2+(a*x2**2+b*x2+c-y2)**2
    print(L)
    for i in range(100000):
        a = a - (2*(a*x1**2+b*x1+c-y1)*(x1**2)+2*(a*x2**2+b*x2+c-y2)*(x2**2))*0.001
        b = b - (2*(a*x1**2+b*x1+c-y1)*(x1)+2*(a*x2**2+b*x2+c-y2)*(x2))*0.001
        c = c - (2*(a*x1**2+b*x1+c-y1)+2*(a*x2**2+b*x2+c-y2))*0.001
    L1 = (a * x1 ** 2 + b * x1 + c - y1) ** 2 + (a * x2 ** 2 + b * x2 + c - y2) ** 2
    print(L1,'L1')
    print(a,b,c)
    return a,b,c

def testfunction(f):
    p1 = [5, 3]
    p2 = [-3, -9]
    a, b, c = f(p1, p2)
    x = np.arange(-20, 20)
    y = a * x ** 2 + b * x + c
    plt.title("Matplotlib demo")
    plt.xlabel("x axis caption")
    plt.ylabel("y axis caption")
    plt.plot(x, y)
    [a1, b1] = p1 
    [a2, b2] = p2
    plt.plot(a1, b1, 'ob')
    plt.plot(a2, b2, 'ob')
    plt.show()

执行testfunction则得到实验结果

  testfunction(No_rugularization)#实验结果表明所得的系数绝对值很大

所学到的曲线：

结果为：a=1726.5490931668319,b= -3451.5981863336674,c= -25902.736397502467

1.用了正则化的例子

损失函数为 $L=[a(X1{)}^2+b(x1)+c-y1{]}^2+[a(X2{)}^2+b(x2)+c-y2{]}^2+a^2+b^2+c^2$
$$

def ZhengzehuaL2(e,f):
   x1=e[0]
   y1=e[1]
   x2=f[0]
   y2=f[1]
   a=-1000000
   c,b=1000 ,1000#给一个较大初始值
   L=(a*x1**2+b*x1+c-y1)**2+(a*x2**2+b*x2+c-y2)**2+a**2+b**2+c**2
   print(L)
   for i in range(100000):#学习率设为0.001
       a = a - (2*(a*x1**2+b*x1+c-y1)*(x1**2)+2*(a*x2**2+b*x2+c-y2)*(x2**2)+a*2)*0.001
       b = b - (2*(a*x1**2+b*x1+c-y1)*(x1)+2*(a*x2**2+b*x2+c-y2)*(x2)+b*2)*0.001
       c = c - (2*(a*x1**2+b*x1+c-y1)+2*(a*x2**2+b*x2+c-y2)+c*2)*0.001
   L1 = (a * x1 ** 2 + b * x1 + c - y1) ** 2 + (a * x2 ** 2 + b * x2 + c - y2) ** 2
   print(L1,'L1')
   print(a,b,c)
   return a,b,c

执行testfunction再得到实验结果

  testfunction(ZhengzehuaL2)#实验结果表明  正则化 让所得的系数绝对值非常小

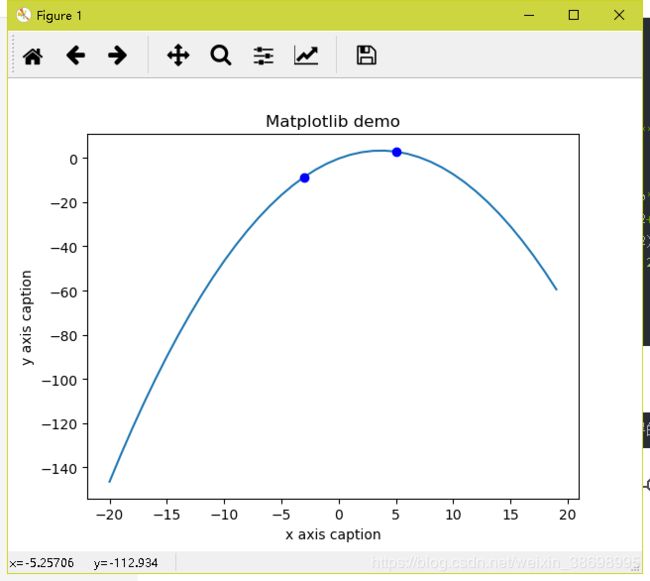
结果为：a= -0.26734786263984833，b=1.9645605639267882，c= -0.27976459936624853
实验结果表明：正则化 让所得的系数绝对值非常小