Python3实现单目标粒子群算法(PSO)
关于PSO的基本知识......就说一下算法流程
1) 初始化粒子群;
随机设置各粒子的位置和速度,默认粒子的初始位置为粒子最优位置,并根据所有粒子最优位置,选取群体最优位置。
2) 判断是否达到迭代次数;
若没有达到,则跳转到步骤3)。否则,直接输出结果。
3) 更新所有粒子的位置和速度;
4) 计算各粒子的适应度值。
将粒子当前位置的适应度值与粒子最优位置的适应度值进行比较,决定是否更新粒子最优位置;将所有粒子最优位置的适应度值与群体最优位置的适应度值进行比较,决定是否更新群体最优位置。然后,跳转到步骤2)。
直接扔代码......(PS:1.参数动态调节;2.例子是二维的)
首先,是一些准备工作...
# Import libs
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# Constant definition
MIN_POS = [-5, -5] # Minimum position of the particle
MAX_POS = [5, 5] # Maximum position of the particle
MIN_SPD = [-0.5, -0.5] # Minimum speed of the particle
MAX_SPD = [1, 1] # Maximum speed of the particle
C1_MIN = 0
C1_MAX = 1.5
C2_MIN = 0
C2_MAX = 1.5
W_MAX = 1.4
W_MIN = 0然后是PSO类
# Class definition
class PSO():
"""
PSO class
"""
def __init__(self,iters=100,pcount=50,pdim=2,mode='min'):
"""
PSO initialization
------------------
"""
self.w = None # Inertia factor
self.c1 = None # Learning factor
self.c2 = None # Learning factor
self.iters = iters # Number of iterations
self.pcount = pcount # Number of particles
self.pdim = pdim # Particle dimension
self.gbpos = np.array([0.0]*pdim) # Group optimal position
self.mode = mode # The mode of PSO
self.cur_pos = np.zeros((pcount, pdim)) # Current position of the particle
self.cur_spd = np.zeros((pcount, pdim)) # Current speed of the particle
self.bpos = np.zeros((pcount, pdim)) # The optimal position of the particle
self.trace = [] # Record the function value of the optimal solution
def init_particles(self):
"""
init_particles function
-----------------------
"""
# Generating particle swarm
for i in range(self.pcount):
for j in range(self.pdim):
self.cur_pos[i,j] = rd.uniform(MIN_POS[j], MAX_POS[j])
self.cur_spd[i,j] = rd.uniform(MIN_SPD[j], MAX_SPD[j])
self.bpos[i,j] = self.cur_pos[i,j]
# Initial group optimal position
for i in range(self.pcount):
if self.mode == 'min':
if self.fitness(self.cur_pos[i]) < self.fitness(self.gbpos):
gbpos = self.cur_pos[i]
elif self.mode == 'max':
if self.fitness(self.cur_pos[i]) > self.fitness(self.gbpos):
gbpos = self.cur_pos[i]
def fitness(self, x):
"""
fitness function
----------------
Parameter:
x :
"""
# Objective function
fitval = 5*np.cos(x[0]*x[1])+x[0]*x[1]+x[1]**3 # min
# Retyrn value
return fitval
def adaptive(self, t, p, c1, c2, w):
"""
"""
#w = 0.95 #0.9-1.2
if t == 0:
c1 = 0
c2 = 0
w = 0.95
else:
if self.mode == 'min':
# c1
if self.fitness(self.cur_pos[p]) > self.fitness(self.bpos[p]):
c1 = C1_MIN + (t/self.iters)*C1_MAX + np.random.uniform(0,0.1)
elif self.fitness(self.cur_pos[p]) <= self.fitness(self.bpos[p]):
c1 = c1
# c2
if self.fitness(self.bpos[p]) > self.fitness(self.gbpos):
c2 = C2_MIN + (t/self.iters)*C2_MAX + np.random.uniform(0,0.1)
elif self.fitness(self.bpos[p]) <= self.fitness(self.gbpos):
c2 = c2
# w
#c1 = C1_MAX - (C1_MAX-C1_MIN)*(t/self.iters)
#c2 = C2_MIN + (C2_MAX-C2_MIN)*(t/self.iters)
w = W_MAX - (W_MAX-W_MIN)*(t/self.iters)
elif self.mode == 'max':
pass
return c1, c2, w
def update(self, t):
"""
update function
---------------
Note that :
1. Update particle position
2. Update particle speed
3. Update particle optimal position
4. Update group optimal position
"""
# Part1 : Traverse the particle swarm
for i in range(self.pcount):
# Dynamic parameters
self.c1, self.c2, self.w = self.adaptive(t,i,self.c1,self.c2,self.w)
# Calculate the speed after particle iteration
# Update particle speed
self.cur_spd[i] = self.w*self.cur_spd[i] \
+self.c1*rd.uniform(0,1)*(self.bpos[i]-self.cur_pos[i])\
+self.c2*rd.uniform(0,1)*(self.gbpos - self.cur_pos[i])
for n in range(self.pdim):
if self.cur_spd[i,n] > MAX_SPD[n]:
self.cur_spd[i,n] = MAX_SPD[n]
elif self.cur_spd[i,n] < MIN_SPD[n]:
self.cur_spd[i,n] = MIN_SPD[n]
# Calculate the position after particle iteration
# Update particle position
self.cur_pos[i] = self.cur_pos[i] + self.cur_spd[i]
for n in range(self.pdim):
if self.cur_pos[i,n] > MAX_POS[n]:
self.cur_pos[i,n] = MAX_POS[n]
elif self.cur_pos[i,n] < MIN_POS[n]:
self.cur_pos[i,n] = MIN_POS[n]
# Part2 : Update particle optimal position
for k in range(self.pcount):
if self.mode == 'min':
if self.fitness(self.cur_pos[k]) < self.fitness(self.bpos[k]):
self.bpos[k] = self.cur_pos[k]
elif self.mode == 'max':
if self.fitness(self.cur_pos[k]) > self.fitness(self.bpos[k]):
self.bpos[k] = self.cur_pos[k]
# Part3 : Update group optimal position
for k in range(self.pcount):
if self.mode == 'min':
if self.fitness(self.bpos[k]) < self.fitness(self.gbpos):
self.gbpos = self.bpos[k]
elif self.mode == 'max':
if self.fitness(self.bpos[k]) > self.fitness(self.gbpos):
self.gbpos = self.bpos[k]
def run(self):
"""
run function
-------------
"""
# Initialize the particle swarm
self.init_particles()
# Iteration
for t in range(self.iters):
# Update all particle information
self.update(t)
#
self.trace.append(self.fitness(self.gbpos))然后是main...
def main():
"""
main function
"""
for i in range(1):
pso = PSO(iters=100,pcount=50,pdim=2, mode='min')
pso.run()
#
print('='*40)
print('= Optimal solution:')
print('= x=', pso.gbpos[0])
print('= y=', pso.gbpos[1])
print('= Function value:')
print('= f(x,y)=', pso.fitness(pso.gbpos))
#print(pso.w)
print('='*40)
#
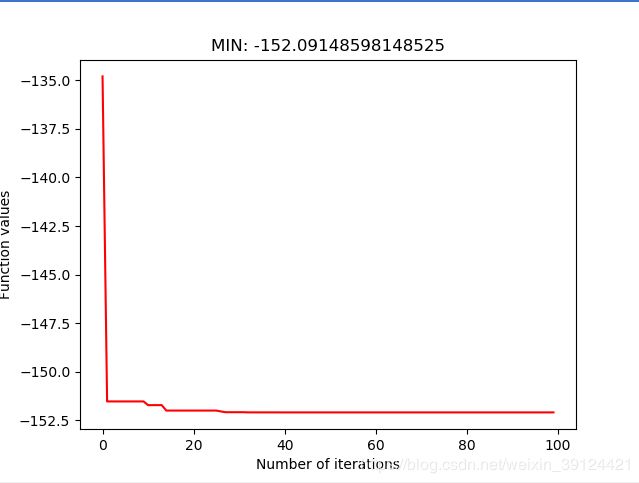
plt.plot(pso.trace, 'r')
title = 'MIN: ' + str(pso.fitness(pso.gbpos))
plt.title(title)
plt.xlabel("Number of iterations")
plt.ylabel("Function values")
plt.show()
#
input('= Press any key to exit...')
print('='*40)
exit()
if __name__ == "__main__":
main()
最后是计算结果,完美结束!!!