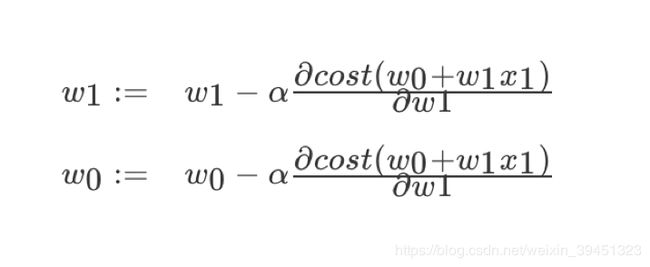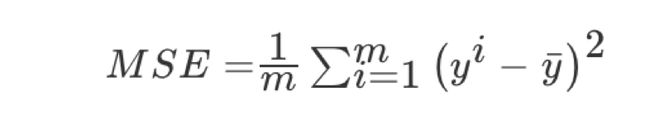机器学习实战之回归与聚类算法

1. 线性回归

学习目标:
        记忆线性回归的原理过程
        应用LinearRegression或SGDRegressor实现回归预测
        记忆回归算法的评估标准及其公式
应用
        波士顿房价预测

1.1 线性回归的原理

1.1.1 线性回归应用场景

房价预测
销售额度预测
金融：贷款额度预测、利用线性回归以及系数分析因子和选股

1.1.2 什么是线性回归

定义与公式:
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
特点：只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归

那么怎么理解呢？我们来看几个例子.
期末成绩：0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
上面两个例子，我们看到特征值与目标值之间建立的一个关系，这个可以理解为回归方程。
线性关系:

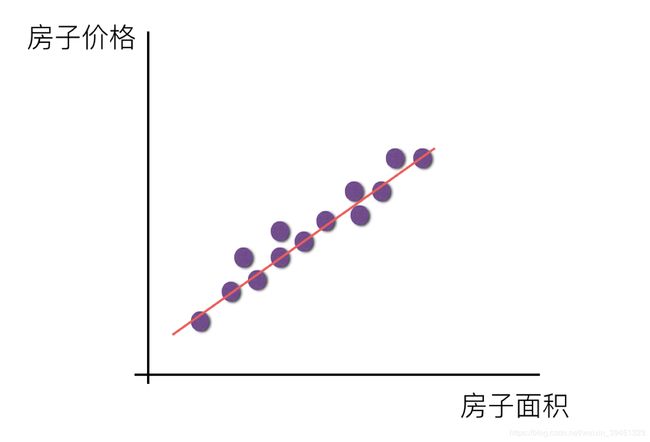
注释：如果在单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系

更高维度的我们不用自己去想，记住这种关系即可

非线性关系:

1.2 线性回归的损失和优化原理（理解记忆）

假设刚才的房子例子，真实的数据之间存在这样的关系:

真实关系：真实房子价格 = 0.02×中心区域的距离 + 
0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

那么现在呢，我们随意指定一个关系（猜测）

机指定关系：预测房子价格 = 0.25×中心区域的距离 + 
0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率

请问这样的话，会发生什么？真实结果与我们预测的结果之间是不是存在一定的误差呢？类似这个样子

那么存在这个误差，我们将这个误差给衡量出来

1.2.1 损失函数

总损失定义为：

y_i为第i个训练样本的真实值
h(x_i)为第i个训练样本特征值组合预测函数
又称最小二乘法

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！

1.2.2 优化算法

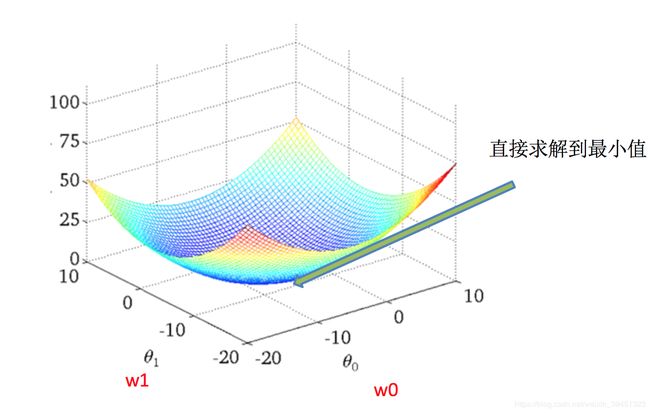
如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）
线性回归经常使用的两种优化算法

(1)正规方程

理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

(2)梯度下降(Gradient Descent)

理解：α为学习速率，需要手动指定（超参数），α旁边的整体表示方向

沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值

使用：面对训练数据规模十分庞大的任务 ，能够找到较好的结果

我们通过两个图更好理解梯度下降的过程


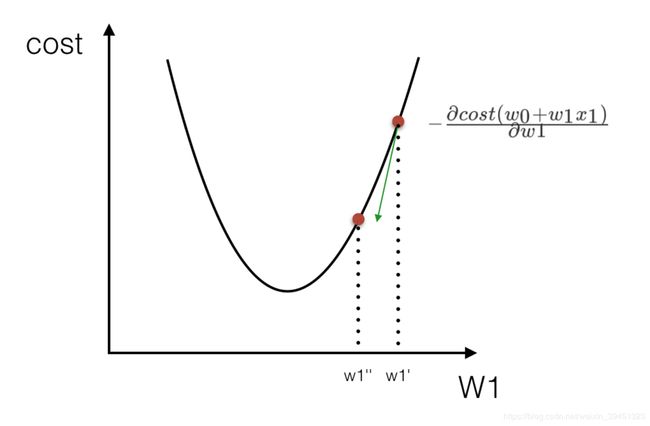
所以有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力

1.3 线性回归API

sklearn.linear_model.LinearRegression(fit_intercept=True)
        通过正规方程优化
        fit_intercept：是否计算偏置
        LinearRegression.coef_：回归系数
        LinearRegression.intercept_：偏置
sklearn.linear_model.SGDRegressor(loss=“squared_loss”,         fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
        通过使用SGD优化
        loss:损失类型 *
        fit_intercept：是否计算偏置
        learning_rate : string, optional
                学习率填充
                ‘constant’: eta = eta0
                ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
                ‘invscaling’: eta = eta0 / pow(t, power_t)
                power_t=0.25:存在父类当中
        loss:SGDRegressor.coef_：回归系数
        loss:SGDRegressor.intercept_：偏置

1.4 波士顿房价预测

数据介绍:

给定的这些特征，是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用，
只需要使用这些特征。到后面量化很多特征需要我们自己去寻找

1.4.1 分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。同时我们对目标值也需要做标准化处理。

        l数据分割与标准化处理
        l回归预测
        l线性回归的算法效果评估

1.4.2 回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

注：y^i为预测值，¯y为真实值

sklearn.metrics.mean_squared_error(y_true, y_pred)
        l均方误差回归损失
        ly_true:真实值
        ly_pred:预测值
        lreturn:浮点数结果

1.4.3 代码

下面代码,将正规方程,梯度下降,岭回归,模型加载与保存内容包含.
岭回归,模型加载与保存在后续讲解

from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.externals import joblib

def mylinearregression():
    """
    线性回归预测房子价格
    :return:
    """
    #获取数据进行分割
    lb = load_boston()
    # print(lb.data)
    # print(lb.target)

    # 对数据集进行划分
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.3, random_state=24)

    # 需要做标准化处理对于特征值处理
    std_x = StandardScaler()

    x_train = std_x.fit_transform(x_train)
    x_test = std_x.fit_transform(x_test)

    # 使用线性模型进行预测
    # 使用正规方程求解
    lr = LinearRegression(fit_intercept=True)

    # fit之后已经得出参数结果
    lr.fit(x_train, y_train)

    #保存模型
    joblib.dump(lr, "mylinearession.pkl")

    #直接加载模型去预测
    lr_model = joblib.load("mylinearession.pkl")
    print("预测未知的测试集结果：", lr_model.predict(x_test))
    print("正规方程计算出的权重", lr.coef_)
    print("正规方程计算出的偏置", lr.intercept_)

    #调用predict去预测目标值
    y_lr_predict = lr.predict(x_test)
   # print("测试集预测的价格为：", y_lr_predict[:100])

    #调用均方误差去评估LinearRegression
    error = mean_squared_error(y_test,y_lr_predict) #平均每个样本的误差为根号（error）
    print("Lineargression的结果预测误差为：", error)


    # 梯度下降进行预测
    #sgd = SGDRegressor(loss ="squared_loss", fit_intercept=True, learning_rate="invscaling")
    #修改学习率为0.1,0.01,0.001
    sgd = SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate="constant", eta0=0.01)

    #得出权重和偏置
    sgd.fit(x_train, y_train)

    print("SGD梯度下降计算出的权重：", sgd.coef_)
    print("SGD梯度下降计算出的偏置：", sgd.intercept_)

    y_sgd_predict = sgd.predict(x_test)
    #print("SGD的预测的结果为：", y_sgd_predict)

    #调用均方误差法去评估SGDRegression的结果
    sgd_error = mean_squared_error(y_test, y_sgd_predict)
    print("梯度下降的结果误差为：", sgd_error)

    #使用带有L2正则化的线性回归去进行预测
    rd = Ridge(alpha=1.0)

    rd.fit(x_train, y_train)

    print("岭回归计算出的权重：", sgd.coef_)
    print("岭回归计算出的偏置：", sgd.intercept_)


    y_rd_predict = rd.predict(x_test)
    #print("RD的预测的结果为：", y_rd_predict)

    #调用均方误差法去评估RDRegression的结果
    rd_error = mean_squared_error(y_test, y_rd_predict)
    print("岭回归的结果误差为：", rd_error)

    return None

if __name__ == "__main__":
    mylinearregression()

输出结果:(此数据集样本量较小)

预测未知的测试集结果： [22.80437323 18.84441566 25.96701769 21.15248871 20.82374141 35.83699597
 22.91812119 16.43679892  9.0073492  30.16529437 23.46704249 18.56528243
 15.40946633 27.58637857 22.62756193 23.11824278 29.37783524 32.83389347
 34.51234923 26.13174428 18.15211678 27.38565363 12.00390113 24.09856898
 21.35477094 22.73516527 31.37906212 31.19181166 16.92491453 23.76361277
 28.28120308 24.94985213 28.83924674 18.84677372  8.78340455 27.68185238
 11.86562929 21.08335679 40.50399736 23.55544564 21.81146935 32.19839637
 21.14781545 17.46433465 32.75477012  9.36419424 18.94083256 25.18739322
 23.75251365 22.04772995 26.19147034 31.74328657 43.57367877 16.42930155
 27.79271915 29.85511169 22.18436927 20.34744799 25.87695973 12.90723091
 17.97914139 16.1949619  22.81135116 13.40361652 23.94796421 12.16831964
 26.27261541 18.93731591 17.66022128  6.08699026 33.21306728 23.35146235
 20.80770512 17.86668462  0.32186025 28.23761372 34.92367238 17.22888057
 27.78068757 16.68808569  7.27673083 18.65391261 19.12265262 25.76330064
 20.96532877 26.3994086  21.05263388 16.23602844 18.44384403 22.44012972
 16.26931348 24.44125516 14.28108039 23.42313695 34.6679564  38.77649579
 23.39935172 25.89956528 26.73031473 39.6648778  13.90431089 25.68690604
 12.25347713 20.68276398 11.06213696 23.15342979 22.12847608 35.6898763
 20.95673519 33.27928147 23.39217083 18.27671068 13.85501343 24.18086641
 30.87191775 16.82046029 15.42556176 29.96308931 34.72845749 42.00336648
 25.7697528  15.81232959 15.34927023 34.40822001 30.18811502 26.99867434
  8.09054517 14.28976025 22.67427044 22.10275249 18.73361068 20.53918438
 38.61185874  7.99702869 25.24272012 29.23206342 23.10302994 35.60214834
 29.73659118 20.71408374 20.71403776 33.34223444 16.5313983  21.67943858
 20.03564076 18.14071246 20.70991604  7.21170352 23.92345761 27.82677193
 26.23200452 21.18612452]
正规方程计算出的权重 [-0.42628394  0.89158868 -0.06427072  0.73607731 -1.52658138  3.08365962
 -0.24548381 -3.0339212   2.06871031 -1.96790672 -1.87229373  0.95515481
 -3.68947008]
正规方程计算出的偏置 22.85112994350283
Lineargression的结果预测误差为： 22.133195225521856
SGD梯度下降计算出的权重： [-0.45504698  0.91580365 -0.37830456  1.16602262 -1.68655757  3.42080467
 -0.4316715  -2.75613726  1.62172842 -1.33889177 -1.3735219   1.18789199
 -3.9156061 ]
SGD梯度下降计算出的偏置： [22.82500534]
梯度下降的结果误差为： 24.107922762443227
岭回归计算出的权重： [-0.45504698  0.91580365 -0.37830456  1.16602262 -1.68655757  3.42080467
 -0.4316715  -2.75613726  1.62172842 -1.33889177 -1.3735219   1.18789199
 -3.9156061 ]
岭回归计算出的偏置： [22.82500534]
岭回归的结果误差为： 22.16837481284264

Process finished with exit code 0

1.4.4 正规方程和梯度下降对比

文字对比:

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

选择：
    小规模数据：
                LinearRegression(不能解决拟合问题)
                岭回归
    大规模数据：SGDRegressor

1.4.5 线性回归总结

线性回归的损失函数-均方误差
线性回归的优化方法
    正规方程
    梯度下降
线性回归的性能衡量方法-均方误差
sklearn的SGDRegressor API 参数

1.5 欠拟合与过拟合

学习目标:
    说明线性回归（不带正则化）的缺点
    说明过拟合与欠拟合的原因以及解决方法
问题：训练数据训练的很好啊，误差也不大，为什么在测试集上面有问题呢？
当算法在某个数据集当中出现这种情况，可能就出现了过拟合现象。

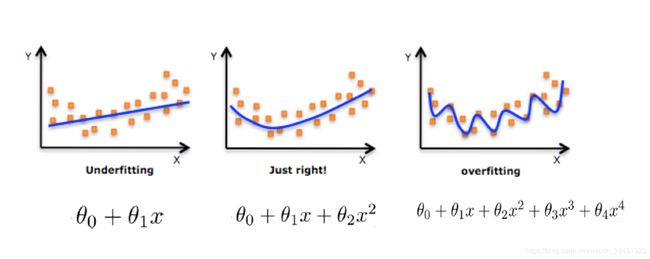
1.5.1 什么是过拟合与欠拟合

欠拟合

过拟合:

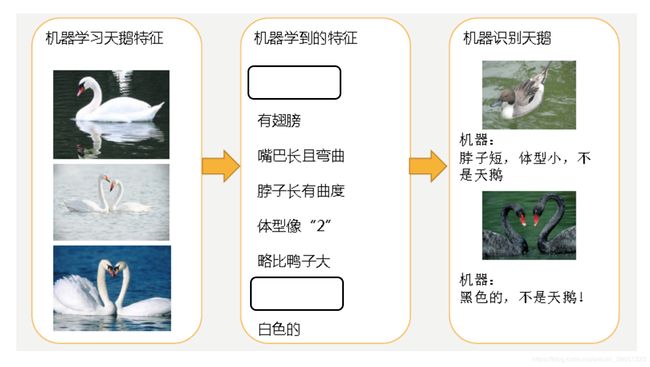
分析
    第一种情况：因为机器学习到的天鹅特征太少了，导致区分标准太粗糙，不能准确识别出天鹅。
    第二种情况：机器已经基本能区别天鹅和其他动物了。然后，很不巧已有的天鹅图片全是白天鹅的，于是机器经过学习后，会认为天鹅的羽毛都是白的，以后看到羽毛是黑的天鹅就会认为那不是天鹅。
定义:
    过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
    欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

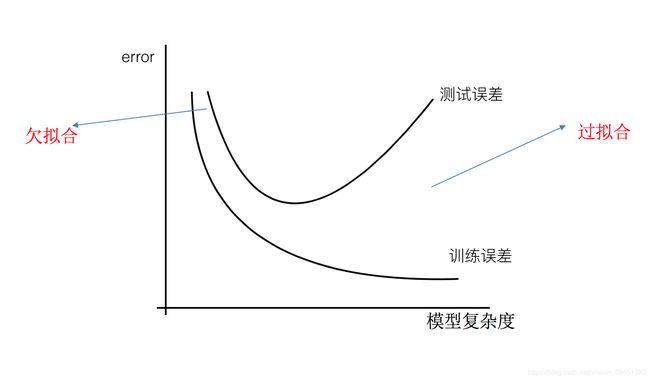
那么是什么原因导致模型复杂？线性回归进行训练学习的时候变成模型会变得复杂，这里就对应前面再说的线性回归的两种关系，非线性关系的数据，也就是存在很多无用的特征或者现实中的事物特征跟目标值的关系并不是简单的线性关系。

1.5.2 原因以及解决办法

欠拟合原因以及解决办法:
    原因：学习到数据的特征过少
    解决办法：增加数据的特征数量
过拟合原因以及解决办法:
    原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点
    解决办法：正则化

在这里针对回归，我们选择了正则化。但是对于其他机器学习算法如分类算法来说也会出现这样
的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，
包括之前说的删除、合并一些特征

如何解决？

在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习
的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化
注：调整时候，算法并不知道某个特征影响，而是去调整参数得出优化的结果

1.5.2.1 正则化类别

L2正则化
    作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
    优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
Ridge回归
L1正则化
    作用：可以使得其中一些W的值直接为0，删除这个特征的影响
    LASSO回归

1.5.2.2 拓展-原理(了解)

线性回归的损失函数用最小二乘法，等价于当预测值与真实值的误差满足正态分布时的极大似然估计；
岭回归的损失函数，是最小二乘法+L2范数，等价于当预测值与真实值的误差满足正态分布，且权重值
也满足正态分布（先验分布）时的最大后验估计；LASSO的损失函数，是最小二乘法+L1范数，等价于
等价于当预测值与真实值的误差满足正态分布，且且权重值满足拉普拉斯分布（先验分布）时的最大后
验估计

1.6 线性回归的改进-岭回归

学习目标:
    说明岭回归的原理即与线性回归的不同之处
    说明正则化对于权重参数的影响
    说明L1和L2正则化的区别
应用:
    波士顿房价预测
定义:
岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果

1.6.1 API

sklearn.linear_model.Ridge(alpha=1.0)
    具有l2正则化的线性回归
    alpha:正则化力度，也叫 λ
        λ取值：0~1 1~10
    coef_:回归系数
sklearn.linear_model.RidgeCV(BaseRidgeCV, RegressorMixin)
    具有l2正则化的线性回归，可以进行交叉验证
    coef:回归系数

class _BaseRidgeCV(LinearModel):
    def __init__(self, alphas=(0.1, 1.0, 10.0),
                 fit_intercept=True, normalize=False, scoring=None,
                 cv=None, gcv_mode=None,
                 store_cv_values=False):

1.6.2 正则化程度的变化对结果的影响

正则化力度越大，权重系数会越小
正则化力度越小，权重系数会越大

1.6.3波士顿房价预测

完整运行代码见1.4.3

 #使用带有L2正则化的线性回归去进行预测
    rd = Ridge(alpha=1.0)

    rd.fit(x_train, y_train)

    print("岭回归计算出的权重：", sgd.coef_)
    print("岭回归计算出的偏置：", sgd.intercept_)


    y_rd_predict = rd.predict(x_test)
    #print("RD的预测的结果为：", y_rd_predict)

    #调用均方误差法去评估RDRegression的结果
    rd_error = mean_squared_error(y_test, y_rd_predict)
    print("岭回归的结果误差为：", rd_error)

2. 逻辑回归与二分类

学习目标:
    说明逻辑回归的损失函数
    说明逻辑回归的优化方法
    说明sigmoid函数
c知道逻辑回归的应用场景
    知道精确率、召回率指标的区别
    知道F1-score指标说明召回率的实际意义
    说明如何解决样本不均衡情况下的评估
    了解ROC曲线的意义说明AUC指标大小
    应用classification_report实现精确率、召回率计算
    应用roc_auc_score实现指标计算
应用
    癌症患者预测
逻辑回归是一种分类算法，虽然名字中带有回归。但是它与回归之间有一定的联系。
分类:线性回归(输出连续型) + sigmoid + 正则化(防止逻辑回归过拟合)

2.1 逻辑回归的应用场景

广告点击率
是否为垃圾邮件
是否患病
金融诈骗
虚假账号

2.2 逻辑回归的原理

2.2.1 输入

逻辑回归的输入就是一个线性回归的结果。

2.2.2 激活函数

sigmoid函数

分析：
    线性回归的结果输入到sigmoid函数中；
    输出结果：[0， 1]区间的一个概率值，默认0.5为阈值

逻辑回归的分类是通过属于某个类别的概率值，来判断是否属于某个类别，并且这个类比默认标记为
1（正例），另外的一个类别会标记为0（反例）。（方便计算损失）

理解图：

输出结果解释：假设有A、B两个类别，当输出结果概率值超过0.5，预测判为A（1），否则判为B（0）.
问题：如何衡量预测结果与真实结果的差异？

2.2.3 损失及优化

2.2.3.1损失

逻辑回归的损失称之为**对数似然损失。**公式如下：

根据损失函数log函数图像来理解这个公式：
当y=1时：

如图所示：损失值越大，预测概率越接近0，损失值越小，预测概率越接近1，即接近真实值。

损失函数公式如下：

与信息熵类似。

如图所示，减小损失函数的过程，既是增大P的过程，（红箭头所指），最终使得，预测为正样本的概率越来越接近1，预测为负样本的概率越来越接近0，即预测的准确率越来越高。

2.2.3.1优化

使用梯度下降优化算法，去减少损失函数的值，从而更新线性回归公式中的权重参数，提升原本属于1类别的概率，降低原本属于0类别的概率，使得预测值越来越接近真实值。

2.2.4 逻辑回归API

sklearn.linear_model.LogisticRegression(solver=‘liblinear’, penalty = ‘L2’, C = 1.0)
    solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标准下降法来迭代优化损失函数)
        sag:根据数据集自动选择,随机平均梯度下降
    penalty:正则化种类
    C:正则化粒度

默认将类别数量少的当正例

2.3 案例-癌症细胞预测(良/恶)

数据介绍：

2.3.1 分析

缺失值处理
标准化处理
逻辑回归预测

2.3.2 代码

from sklearn.linear_model import  LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import  classification_report, roc_auc_score
import pandas as pd
import numpy as np

def logistic():
    """
    使用逻辑回归进行肿瘤数据预测
    :return:
    """
    column_name = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

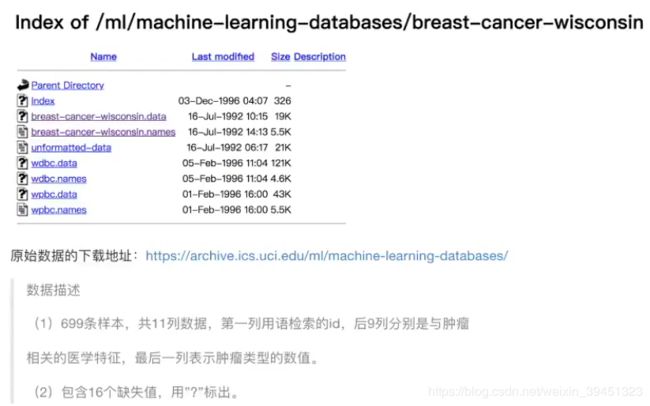
    # 读取数据，处理缺失值
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                names=column_name)

    print(data.shape)
    # 将?替换np.nan
    data = data.replace(to_replace='?', value=np.nan)
    
    #把nan的数据样本丢掉
    data = data.dropna()
    print(data.shape)

    # 分割数据到训练集测试集,0列是样本标号,特征值是从第1-9列,第10列是目标值
    x = data.iloc[:, 1:10]    #特征值
    y = data.iloc[:, 10]      #目标值

    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # 进行标准化（前面的输入也是一个线性回归）
    std = StandardScaler()

    x_train = std.fit_transform(x_train)

    x_test = std.fit_transform(x_test)

    # 逻辑回归进行训练以及预测
    lr = LogisticRegression()

    # 默认会把4（恶性）当做成正例（1）， 会把2（良性）当做成反例（0）
    lr.fit(x_train, y_train)

    #保存模型
    #joblib.dump(lr, "myLogisticRegression.pkl")



    print("逻辑回归计算出的权重：", lr.coef_)
    print("逻辑回归计算出的偏置：", lr.intercept_)

    print("逻辑回归在测试集当中的预测类别：", lr.predict(x_test))

    print("逻辑回归预测的准确率：", lr.score(x_test, y_test))

    # 召回率
    print("预测的召回率为：", classification_report(y_test, lr.predict(x_test), labels=[2, 4], target_names=['良性', '恶性']))

    # 查看我们这个分类在这些癌症数据的AUC指标值，样本不均衡时AUC   指标很重要
    y_test = np.where(y_test > 2.5, 1, 0)

    print("此场景的分类器的AUC指标为", roc_auc_score(y_test, lr.predict(x_test)))

    return None

if __name__ == '__main__':
    logistic()

输出结果:

(699, 11)
(683, 11)
逻辑回归计算出的权重： [[1.14310778 0.35957914 0.76405249 0.80790742 0.1324307  1.35594409
  0.49169604 0.87294869 0.82565586]]
逻辑回归计算出的偏置： [-0.75583961]
逻辑回归在测试集当中的预测类别： [2 2 2 4 2 4 2 4 4 2 2 4 2 2 2 2 4 2 2 4 2 4 2 2 4 2 4 2 2 2 2 2 4 2 4 4 2
 2 2 2 4 2 2 4 2 2 2 2 2 4 2 2 2 4 4 2 4 2 4 2 2 4 2 2 4 4 4 2 2 2 2 2 2 2
 2 2 2 2 2 4 2 2 2 4 4 2 4 2 4 2 2 4 4 2 4 2 2 2 2 2 2 4 4 2 4 2 4 2 2 2 2
 4 2 2 2 4 2 4 2 2 2 2 2 4 4 2 2 4 2 2 2 4 2 2 4 4 2 4 4 2 2 2 4 4 2 4 4 2
 2 2 2 2 2 2 2 2 4 2 4 4 4 2 2 2 2 2 2 2 2 4 2 2 2 2 4 2 4 4 4 4 2 4 4 2 4
 2 2 4 4 4 2 2 2 2 4 4 2 2 2 2 2 4 2 2 4]
逻辑回归预测的准确率： 0.975609756097561
预测的召回率为：               precision    recall  f1-score   support

          良性       0.99      0.97      0.98       137
          恶性       0.94      0.99      0.96        68

   micro avg       0.98      0.98      0.98       205
   macro avg       0.97      0.98      0.97       205
weighted avg       0.98      0.98      0.98       205

此场景的分类器的AUC指标为 0.9780485186775442

Process finished with exit code 0

2.4 分类的评估方法

2.4.1 精确率与召回率

2.4.1.1 混淆矩阵

    在分类任务下，预测结果（Predicted Condition）与正确标记（True Condition）之间存在四种不同的组合，构成混淆矩阵（适用于多分类）。
如下图所示：

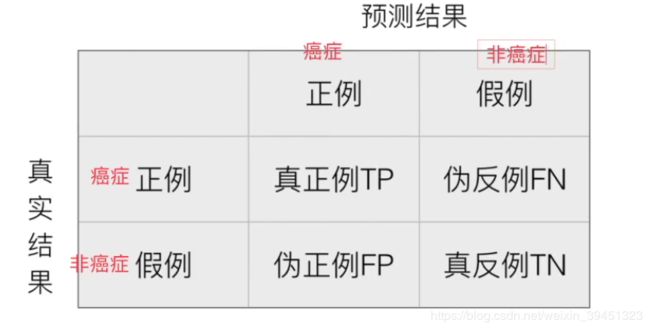
2.4.1.2 精确率（Precision）与召回率（Recall）

• 精确率：预测结果为正例的样本中，真正为正例的比例。
  
• 召回率：真正为正例的样本中，预测结果为正例的比例（对正样本的区分能力）
  
  以癌细胞预测举例：
  总共100个样本，癌症30个样本，非癌症70个样本·。

2.4.2 分类评估报告API

 print("预测的召回率为：", 
 classification_report(y_test, 
 lr.predict(x_test),
 labels=[2, 4], 
 target_names=['良性', '恶性']))

假设有这样一个情况，如果99个样本癌症，一个样本非癌症。无论怎样全部预测为癌症（正例），这样准确率为99%，召回率为100%，但这个分类器并不好（需考察AUC指标），这就是样本不均衡下的评估问题。

2.4.3 ROC曲线和AUC指标

2.4.3.1 TPR与FPR

• TPR = TP/（TP +FN）
    所有真实类别为1的样本中，预测为1的比例。

• FPR = FP/（FP +FN）
    所有真实类别为0的样本中，预测为1的比例。

2.4.3.2 ROC曲线

• ROC曲线的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示的意义是：对于不论是真是类别1还是0的样本，分类预测为1的概率是相等的，测试AUC=0.5，AUC值为面积值。
  

2.4.3.3 AUC指标

• AUC的概率意义是，随机取一对正负样本，正样本得分大于负样本的概率。
• AUC的最小值为0.5，最大值为1，取值越高越好。
• AUC=1，完美分类器，采用这个模型预测试，不管设定什么阈值，都能得出完美预测。
• 05

2.4.3.4 AUC计算API

#0.5~1之间,越接近1越好
y_test = np.where(y_test > 2.5, 1, 0)

print("此场景的分类器的AUC指标为", roc_auc_score(y_test, lr.predict(x_test)))

2.4.3.5 总结

• AUC只能用来评价二分类
• AUC非常适合评价样本不均衡中分类器的性能
• AUC会 比较预测出来的概率，而不仅仅是标签值。

2.5 模型保存与加载

学习目标:
        应用joblib实现模型保存与加载
当训练或者计算好一个模型后,如果其他人要用此模型进行预测,就要先保存好模型.(主要保存算法参数)

2.5.1 sklearn模型的保存和加载API

• from sklearn.externals import joblib
          保存:joblib.dump(rf, “test.pkl”)
          j加载:estimator = joblib(“test.pkl”)

2.5.2 sklearn模型的保存和加载案例

完整代码见1.4.3

 # fit之后已经得出参数结果
   lr.fit(x_train, y_train)

   #保存模型
   joblib.dump(lr, "mylinearession.pkl")

   #直接加载模型去预测
   lr_model = joblib.load("mylinearession.pkl")
   print("预测未知的测试集结果：", lr_model.predict(x_test))
   print("正规方程计算出的权重", lr.coef_)
   print("正规方程计算出的偏置", lr.intercept_)

3.无监督学习 K-means算法

• 学习目标:
          说明K-means算法原理
          说明K-means性能评估标准轮廓系数
          说明K-means优缺点
  应用:
          instacart用户聚类

3.1. 什么是无监督学习

- 一家广告平台需要根据相似的人口学特征和购买习惯将美国人口分成不同的小组,以便广告客户可以通过有关联的广告接触到它么呢用户.
- Airbnb需要将自己的房屋清单分成不同的社区,以便用户能更轻松的查阅这些清单.
- 一个数据科学团队需要降低一个大型数据集维度的数量,以便简化模型降低文件大小.

我们可以怎样更有用的对其进行归纳和分组?我们可以怎样以一种压缩格式有效的表征数据?这些都是无监督学习的目标,之所以称之为无监督,是因为这是从无标签的数据开始学习的.

3.2 无监督学习包含算法

• 聚类
          K-means(K均值聚类)

## 3.3 K-means原理
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190524143632160.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl8zOTQ1MTMyMw==,size_16,color_FFFFFF,t_70)

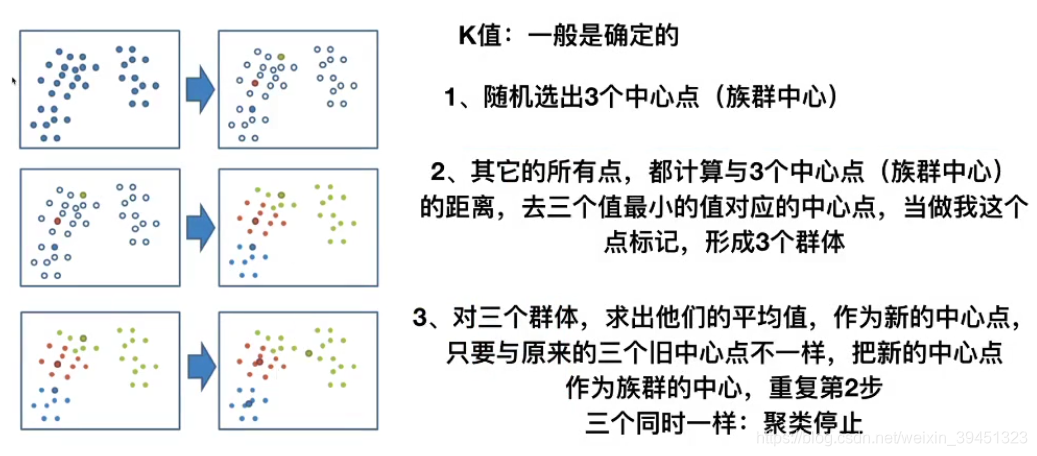
3.3 K-meansAPI

3.4 代码

from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import pandas as pd

#读取4张表
prior = pd.read_csv("./data/instacart/order_products__prior.csv")
products = pd.read_csv("./data/instacart/products.csv")
orders = pd.read_csv("./data/instacart/orders.csv")
aisles = pd.read_csv("./data/instacart/aisles.csv")

# 合并四张表到一张表
#on指定两张表共同拥有的键 内连接
mt = pd.merge(prior, products, on=['product_id', 'product_id'])
mt1 = pd.merge(mt, orders, on=['order_id', 'order_id'])
mt2 = pd.merge(mt1, aisles, on=['aisle_id', 'aisle_id'])

# 进行交叉表变换,pd.crosstab 统计用户与物品之间的次数关系（统计次数）
user_sisle_cross = pd.crosstab(mt2['user_id'], mt2['aisle'])

# PCA进行主成分分析
pc = PCA(n_components=0.95)
data = pc.fit_transform(user_sisle_cross)
print(data)
print(data.shape)

#为了减少运行时间,去部分用户做聚类测试
cusumer = data[:500]

##对该商场用户做聚类分析
#聚成4个群体
km = KMeans(n_clusters=4)

#聚类算法训练
km.fit(cusumer)

#得出每个用户在群体当中的目标值
predict = km.predict(cusumer)
print(predict)
print(silhouette_score(cusumer, predict))

输出结果:

[[-24.21565874   2.4294272   -2.46636975 ...  -0.08877715  -0.38087761
    0.21568831]
 [  6.46320806  36.75111647   8.38255336 ...   1.912145     1.79468946
   -0.70142249]
 [ -7.99030162   2.40438257 -11.03006405 ...  -0.72188348  -1.15719089
   -0.23704277]
 ...
 [  8.61143331   7.70129866   7.95240226 ...   0.23971061  -0.78590175
   -2.65945606]
 [ 84.08621987  20.41873398   8.05410372 ...  -1.66893212   0.5042934
    3.82546312]
 [-13.95345619   6.64621821  -5.23030367 ...  -1.64144758  -3.39233648
   -0.31410713]]
(206209, 44)
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 0
 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1
 0 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 0 1 1 1 0 1 1
 1 1 1 3 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 1 1 2 1 1 1 0 1 1 1 1 1 1 1 1
 3 1 1 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 2 0 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 2 1 1 1 1 1 1 1 0 1 3 1 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 2 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1
 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 2
 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 1 3 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1]
0.5967540245573874

Process finished with exit code 0

3.5聚类算法的评估标准

轮廓系数:

轮廓系数越接近于1越好。