2019-mathorcupB题-环形穿梭机调度模型(思路篇)
前言
此次2019年的mathorcup杯B题和18年建模国赛题目类似,都是关于环形穿梭机(RGV)的调度问题,这里主要以mathorcup杯的赛题来讲解模型的建立部分,关于国赛的相关内容会在后续介绍。
RGV介绍
关于赛题详情请参见mathorcup官网,这里简单介绍一下RGV系统的构成。
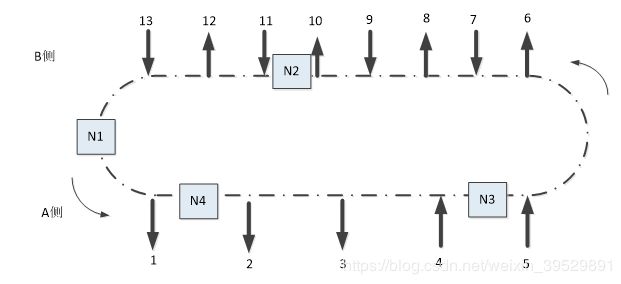
有N辆穿梭车在轨道上跑,每次只能装载一个货物,在A侧上货口的上货的货物要求在B侧出货口运出,而在B侧上货的货物同样只能在A侧出货口运出。
通过对题目的分析不难发现,我们唯一能对整个RGV系统施加的影响只有穿梭车下一次装货或者卸货的窗口,假设每次每辆RGV都能选择对整个系统最有利的装/卸窗口,那么最后得到的结果便是题目要求的最优解。
(1)A、B侧进出口集合
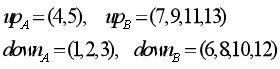
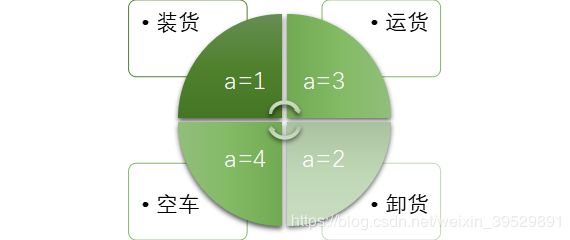
(2)穿梭车当前状态
环形轨道上小车分为正在装货、运货中、进行卸货、空车四种状态,用 a a a表示,穿梭车从一种状态转移至下一状态的时间记为 b b b,穿梭车的窗口记为 c c c,针对穿梭车当前装卸状态设置穿梭车状态函数。
图4穿梭车运行状态
第 i i i辆穿梭车当前状态 s t a t u s i status_i statusi 为:

(3)穿梭机在两两进出货口之间行驶路程
首先针对环形穿梭车系统的A、B两侧的进货口和出货口分别设置编号,以A侧的出货口3为起点1,根据逆时针方向依次编号。
动态规划是把多阶段过程转化成一系列单阶段问题,是研究多阶段决策优化问题的方法,本文利用动态规划求解两两地址间最短距离。根据题意进货口、出货口均匀分布在A、B两侧条件进行计算相关数据,计算相邻进出口之间距离:
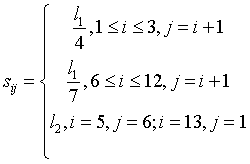
由穿梭机匀速行驶可得状态转移方程:
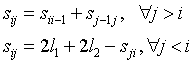
RGV调度模型的建立
1.决策模型的建立
本文的决策目标为系统中最迟完成任务的穿梭车完成搬运货物的总时间,决策目标的最小值即为决策模型的目标函数。决策变量 N e s t Nest Nest为小车下一个的窗口编号,约束条件为最终所有进货窗口货物量为0。
目标函数:
决策变量 N e x t Next Next:
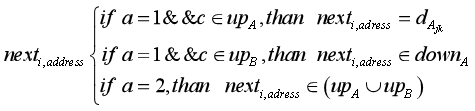
约束条件:
Step1 构建单辆穿梭车状态转移函数:
单辆穿梭车状态转移函数表示单辆穿梭车在不考虑堵塞的条件下由当前状态转化为下一时刻的状态的过程。
单辆穿梭车状态转移函数:
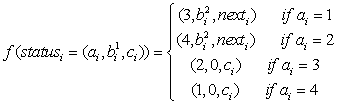
每辆穿梭机转移时间为: b i 1 b^1_i bi1
将第辆穿梭车由当前状态到下一时刻状态所用时间记为 T i T_i Ti,令第 i i i次整体状态转移时间 T i T^i Ti为所有穿梭车状态转移的最短时间。记此时唯一完成状态转移的小车编号为 i = m i n I i i=minI_i i=minIi,第次整体状态转移时间:
在允许超车的情况下,堵塞时间即为超车时间,将此时超车时间记为 w a i t wait wait,此时根据
第 i i i次整体状态转移时间以及单穿梭车状态转移函数得出第 i i i次整体状态转移函数 F 1 ( s t a t u s i ) F_1(status^i) F1(statusi),即 F 1 ( s t a t u s i ) F_1(status^i) F1(statusi)控制每次整体转移仅有一辆穿梭车发生状态转移。
则在允许超车情况下,第 i i i次整体状态转移方程:
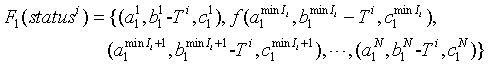
整体状态转移时间与单辆穿梭车转移时间关系:
第 i i i次整体状态转移时间为 T i = m i n ( T 1 i + w a i t 1 , T 2 i + w a i t 2 , … … , T N i + w a i t N ) T^i=min(T^i_1+wait_1,T^i_2+wait_2,……,T^i_N+wait_N) Ti=min(T1i+wait1,T2i+wait2,……,TNi+waitN),则此时唯一完成状态转移的穿梭车编号为 m i n I i min I_i minIi。
Step3 计算每次整体状态转移的时间
当 a i = 1 o r 2 a_i=1or2 ai=1or2时, w a i t i wait_i waiti为0;当 a i = 3 o r 4 a_i=3or4 ai=3or4且 w a i t i wait_i waiti不为0时,说明小车i发生了阻塞,此时,必然存在小车j在i之前完成转移(否则i无法完成状态转移),所以当 w a i t i wait_i waiti不为0时,![]() 综上所述,可得:
综上所述,可得:
Step4构建回溯函数
整体状态转移函数可能发生超车现象,超车的充分必要条件:
①穿梭机i下一次装卸货物的窗口与当前窗口之间的路径上存在其他穿梭机正在进行上下货物,记为集合A.
②存在穿梭机集合![]() ,满足要求:穿梭机i在到达穿梭机 b l o c k block block正在装卸货物窗口的时间<穿梭机剩余装卸货物的时间。
,满足要求:穿梭机i在到达穿梭机 b l o c k block block正在装卸货物窗口的时间<穿梭机剩余装卸货物的时间。

回溯函数具体流程如如下:
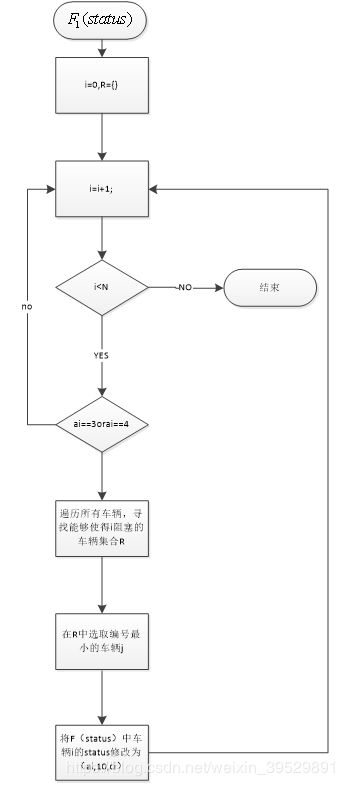
模型的实现
本篇博客主要讲解了模型的建立思路,下面给出一种最简单的模型求解算法,(不是最优的)在下一篇文章2019-mathorcupB题-环形穿梭机调度模型(代码篇)中将根据该算法具体完成模型的实现,
1、基于就近原则的函数 n e x t next next确定。
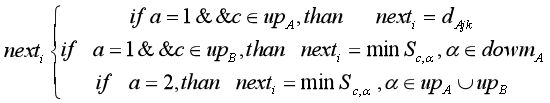
以下是模型求解的结果
| 状态转移次数 | 总共用时(s) | |
|---|---|---|
| N=3 | 1557 | 12699 |
| N=6 | 1437 | 6785.7 |
| N=9 | 536 | 2540.7 |