周志华《机器学习》课后习题系列答案——4.3
周志华《机器学习》课后习题系列答案
(1)课后习题:4.3
试编程实现基于信息熵进行划分选择的决策树算法,并为表4.3中的数据生成一颗决策树

下图是书中按照表4.3生成的数据

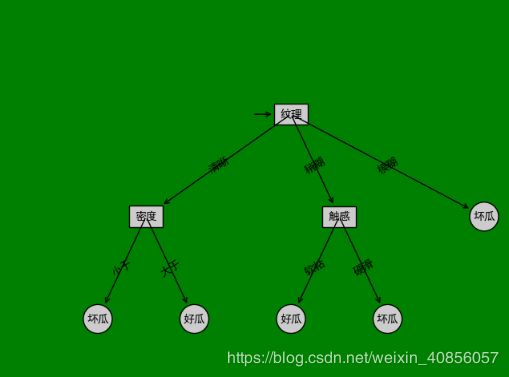
下图是按照书中的思路编程实现的树结构。
现在抛出一个问题:首先我的程序自己仔细调试过,认为没有问题,但是程序将软粘划分为了好瓜,而书中软粘是坏瓜。不过按照书中数据,当纹理=稍糊,只有当触感=软粘的时候才出现了好瓜(即书中第7条数据)。我的这个分类与书中不一致,但是从数据上来看又是合理的。不知道问题是出在哪儿?
下面是程序源代码,分为两个文件:
代码是用python3.7写的,IDE是pycharm
1,划分的python文件
在这里插入代码片
'''
@author: liuyunsheng
@file: D4_3.py
@time: 2019/5/7 15:39
@desc:该文件是为了实现《机器学习》习题4.3:编程实现基于信息熵进行划分选择的决策树算法,并采用表4.3中数据生成一颗决策树
'''
import math
import decisionTreePlot as dtPlot
import numpy as np
def createDataSet():
"""
:return:返回的是创建好的数据集和标签类型
"""
dataset=[['青绿','蜷缩','浊响','清晰','凹陷','硬滑',0.697,0.460,1],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑',0.774,0.376,1],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑',0.634,0.264,1],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑',0.608,0.318,1],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑',0.556,0.215,1],
['青绿','稍蜷','浊响','清晰','稍凹','软粘',0.403,0.237,1],
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘',0.481,0.149,1],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑',0.437,0.211,1],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑',0.666,0.091,0],
['青绿','硬挺','清脆','清晰','平坦','软粘',0.243,0.267,0],
['浅白','硬挺','清脆','模糊','平坦','硬滑',0.245,0.057,0],
['浅白','蜷缩','浊响','模糊','平坦','软粘',0.343,0.099,0],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑',0.639,0.161,0],
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑',0.657,0.198,0],
['乌黑','稍蜷','浊响','清晰','稍凹','软粘',0.360,0.370,0],
['浅白','蜷缩','浊响','模糊','平坦','硬滑',0.593,0.042,0],
['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑',0.719,0.103,0]]
labels=['色泽','根蒂','敲声','纹理','脐部','触感','密度','含糖率','好瓜']
return dataset,labels
def calculateShannonEnt(dataset,labels):
"""
:param dataset:
:return: 返回香农熵
"""
# 1 计算除了密度和含糖率之外的香农熵
length=len(dataset)
yes=0
# 1.1 计算根节点的香农熵
for data in dataset:
if data[-1]==1:
yes=yes+1
p_yes=float(yes/length)
shannonEnt_root=-(p_yes*math.log(p_yes,2)+(1-p_yes)*math.log((1-p_yes),2))
shannonEnt={}
rangeNum=0
if '密度' in labels:
rangeNum=1
if '含糖率' in labels:
rangeNum+=1
for row in range(len(labels)-rangeNum-1):
# 1.2 遍历每一列,计算每一列的香农熵
# featureCounts是记录每个特征的出现的总数以及对应的好瓜次数
featureCounts = {}
for column in range(len(dataset)):
feature=dataset[column][row]
if feature not in featureCounts:
featureCounts[feature] = [0, 0]
featureCounts[feature][0] +=1
if dataset[column][-1]==1:
featureCounts[feature][1] += 1
shannonEnt[row] = 0.0
for key,value in featureCounts.items():
p=value[1]/value[0]
p0=value[0]/length
if p!=0 and p!=1:
shannonEnt0=-float(p0*(p*math.log(p,2)+(1-p)*math.log((1-p),2)))
else:
shannonEnt0=0
shannonEnt[row]+=shannonEnt0
# 2 计算密度和含糖率的熵
final = {}
density={}
sugarContent={}
# 2.1 获得相应行的密度以及含糖率
for column in range(len(dataset)):
if '密度' in labels:
density_index = labels.index('密度')
density[column]=dataset[column][density_index]
if '含糖率' in labels:
sugarcontent_index = labels.index('含糖率')
sugarContent[column]=dataset[column][sugarcontent_index]
density=sorted(density.items(),key=lambda x:x[1])
sugarContent=sorted(sugarContent.items(),key=lambda x:x[1])
# 2.2 计算相邻变量的中间值
middle_density=[]
middle_sugarContent=[]
for num in range(len(density)-1):
middle_density.append((density[num][1]+density[num+1][1])/2)
middle_sugarContent.append((sugarContent[num][1] + sugarContent[num + 1][1]) / 2)
# 2.3 计算相应的信息增益并记录划分点
gain_point_density=calculateENT(shannonEnt_root,middle_density,density,dataset)
gain_point_sugarContent = calculateENT(shannonEnt_root, middle_sugarContent, sugarContent,dataset)
# 排序
gain_point_density=sorted(gain_point_density.items(),key=lambda x:x[1],reverse=True)
gain_point_sugarContent=sorted(gain_point_sugarContent.items(),key=lambda x:x[1],reverse=True)
# 3. 计算熵增益
middle={}
for key, value in shannonEnt.items():
final[labels[key]] = shannonEnt_root - value
if len(gain_point_density)!=0:
final['密度'] = gain_point_density[0][1]
middle['密度']=middle_density[gain_point_density[0][0]]
if len(gain_point_sugarContent)!=0:
middle['含糖率'] = middle_sugarContent[gain_point_sugarContent[0][0]]
final['含糖率'] = gain_point_sugarContent[0][1]
print(middle_density[gain_point_density[0][0]])
return final,middle
def calculateENT(shannonEnt_root,middle,data,dataset):
"""
:param shannonEnt_root:根节点的信息熵
:param middle: 中位数组成的数组
:param data: 由行和值组成的字典集合
:return:返回信息增益
"""
gain={}
for num in range(len(middle)):
# 1,计算左右的个数以及好瓜的个数
# left,right表示middle划分为两类
left = 0
right=0
# num_yes表示左右两边的是好瓜的个数
num_yes_left=0
num_yes_right = 0
middledata=middle[num]
for key in range(len(data)):
if data[key][1] < middledata:
left += 1
if dataset[data[key][0]][-1]==1:
num_yes_left += 1
if data[key][1] > middledata:
right += 1
if dataset[data[key][0]][-1]==1:
num_yes_right += 1
# 2,计算相应的信息熵
p_left=num_yes_left/left
p_right=num_yes_right/right
ent_left=calculate(p_left)
ent_right=calculate(p_right)
# 3,计算信息增益
gain[num]=shannonEnt_root-(left/len(dataset)*ent_left+right*ent_right/len(dataset))
return gain
def calculate(p):
"""
:param p:
:return:返回计算好的信息熵
"""
shannonEnt=0
if p!=0 and p!=1.0:
shannonEnt = -float((p * math.log(p, 2) + (1 - p) * math.log((1 - p), 2)))
return shannonEnt
def getNumbersByString(dataset,feature,labels):
"""
:param feature: 输入的特征,如纹理等
:return:当选中一个特征作为划分节点的时候,需要知道该特征下会有几个特征值,以及每个特征对应的样本编号
"""
featureSet={}
index=labels.index(feature)
for num in range(len(dataset)):
featureName=dataset[num][index]
if featureName not in featureSet:
featureSet[featureName]=[]
featureSet[featureName].append(num)
return featureSet
def getNumbers(dataset,feature,labels,middle):
"""
:param feature: 输入的特征,仅限密度和含糖率
:param middle: 密度和含糖率的二分点
:return:当选中一个特征作为划分节点的时候,需要知道该特征下会有几个特征值,以及每个特征对应的样本编号
"""
featureSet={}
index=labels.index(feature)
for num in range(len(dataset)):
if '小于' not in featureSet:
featureSet['小于']=[]
if '大于' not in featureSet:
featureSet['大于']=[]
if dataset[num][index]2,绘图的python文件
该文件来自于网络,并未做太多的修改,只是增加了显示中文字符需要的包
#!/usr/bin/python
# -*- coding: UTF-8 -*-
'''
Created on Oct 14, 2010
Update on 2017-02-27
Decision Tree Source Code for Machine Learning in Action Ch. 3
Author: Peter Harrington/jiangzhonglian
'''
import matplotlib.pyplot as plt
# 定义文本框 和 箭头格式 【 sawtooth 波浪方框, round4 矩形方框 , fc表示字体颜色的深浅 0.1~0.9 依次变浅,没错是变浅】
decisionNode = dict(boxstyle="square", pad=0.5,fc="0.8")
leafNode = dict(boxstyle="circle", fc="0.8")
arrow_args = dict(arrowstyle="<-")
# 控制显示中文
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是否为dict, 不是+1
if type(secondDict[key]) is dict:
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是不是dict, 求分枝的深度
# ----------写法1 start ---------------
if type(secondDict[key]) is dict:
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
# ----------写法1 end ---------------
# ----------写法2 start --------------
# thisDepth = 1 + getTreeDepth(secondDict[key]) if type(secondDict[key]) is dict else 1
# ----------写法2 end --------------
# 记录最大的分支深度
maxDepth = max(maxDepth, thisDepth)
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
# 获取叶子节点的数量
numLeafs = getNumLeafs(myTree)
# 获取树的深度
# depth = getTreeDepth(myTree)
# 找出第1个中心点的位置,然后与 parentPt定点进行划线
cntrPt = (plotTree.xOff + (1 + numLeafs) / 2 / plotTree.totalW, plotTree.yOff)
# print(cntrPt)
# 并打印输入对应的文字
plotMidText(cntrPt, parentPt, nodeTxt)
firstStr = list(myTree.keys())[0]
# 可视化Node分支点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
# 根节点的值
secondDict = myTree[firstStr]
# y值 = 最高点-层数的高度[第二个节点位置]
plotTree.yOff = plotTree.yOff - 1 / plotTree.totalD
for key in secondDict.keys():
# 判断该节点是否是Node节点
if type(secondDict[key]) is dict:
# 如果是就递归调用[recursion]
plotTree(secondDict[key], cntrPt, str(key))
else:
# 如果不是,就在原来节点一半的地方找到节点的坐标
plotTree.xOff = plotTree.xOff + 1 / plotTree.totalW
# 可视化该节点位置
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
# 并打印输入对应的文字
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1 / plotTree.totalD
def createPlot(inTree):
# 创建一个figure的模版
fig = plt.figure(1, facecolor='green')
fig.clf()
axprops = dict(xticks=[], yticks=[])
# 表示创建一个1行,1列的图,createPlot.ax1 为第 1 个子图,
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
# 半个节点的长度
plotTree.xOff = -0.1 / plotTree.totalW
plotTree.yOff = 0.5
plotTree(inTree, (0.5, 0.5), '')
plt.show()
# # 测试画图
# def createPlot():
# fig = plt.figure(1, facecolor='white')
# fig.clf()
# # ticks for demo puropses
# createPlot.ax1 = plt.subplot(111, frameon=False)
# plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
# plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
# plt.show()
# 测试数据集
def retrieveTree(i):
listOfTrees = [
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
# myTree = retrieveTree(1)
# createPlot(myTree)