啥是卷积神经网络(二)(LeNet-5网络详解)
LeNet-5
- 磨磨唧唧
- 网络介绍
- 输入(Input)
- 隐含层
- 卷积层(Convolutions,C1)
- 池化层(Subsampling,S2)
- 卷积层(Convolutions,C3)
- 池化层(Subsampling,S4)
- 卷积层(Convolutions,C5)
- 全连接层(F6)
磨磨唧唧
上一个随笔说了卷积神经网络中的隐含层及其工作机制,这回以神经网络的开山鼻祖LeNet-5网络为例,对卷积神经网络进行详细的介绍。
网络介绍
先放一张大家都看过的LeNet-5网络结构图,

其实这个图像已经可以很清楚的解释了LeNet-5的网络结构和工作机制。为了更加清晰的理解,我们来一步一步的说。
输入(Input)
输入(Input):将图像数据预处理成大小为32X32的单通道图像。这里的预处理一般就是resize图像和灰度转换。需要知道的是,这个输入层不算LeNet-5网络的结构。
隐含层
LeNet-5的网络包括卷积层(Convolutions,C1)、池化层(Subsampling,S2)、卷积层(C3)、池化层(Subsampling,S4)、卷积层(C5)、全连接层(F6)、输出层(Output),共七层。这里不包含输入层,下面开始逐个进行介绍和解释。
卷积层(Convolutions,C1)
输入图片: 32 × 32 × 1
卷积核大小:5 × 5
卷积核个数:6
输出featuremap大小:28 × 28 × 6 **
神经元数量:4704
可训练参数:(5 × 5 + 1) × 6=156**
连接数:(5×5+1)× 6 × 28 × 28 = 122304
下面对这些数字的由来进行详细的说明。
输入图片、卷积核大小和数量就没啥说的了,这个是文章作者定好的。我们先来说说28 × 28 × 6的输出featuremap是怎么来的。
- 首先是28 × 28,在上面的例子中,输入图片尺寸为32×32,经过一次5×5的卷积之后,图片尺寸变小(这个例子不包含填充Padding)且卷积步长为1。卷积输出特征图的尺寸计算方法如下:

H、Wout表示输出尺寸,H、W表示输入尺寸,Kh、w表示卷积核长宽,1表示偏置项。那么,输出图像尺寸就很容易计算出来:(32 - 5 + 1)= 28 - 输出特征图深度6就不用多说了,就是卷积核的个数,这俩玩意一样大(不懂的可以看我上一个博客)。
然后是神经元数量,这个神经元数量其实就是输出featuremap中元素的总量,也就是28×28×6=4704。
再然后是可训练参数,这个神经元数量其实就是卷积核的参数,记住不要忘记偏置项1,也就是**(5 × 5 + 1) × 6=156**
最后,是连接数的计算,连接数其实是理论上计算的次数,就是
(5 × 5 + 1) × 6 × 28 × 28= 122304
但实际上我们的卷积核只有156个参数,实现参数骤减的原因是权值共享机制。
接下来上一个示意图来详细说明(这个图真的是太难画了)
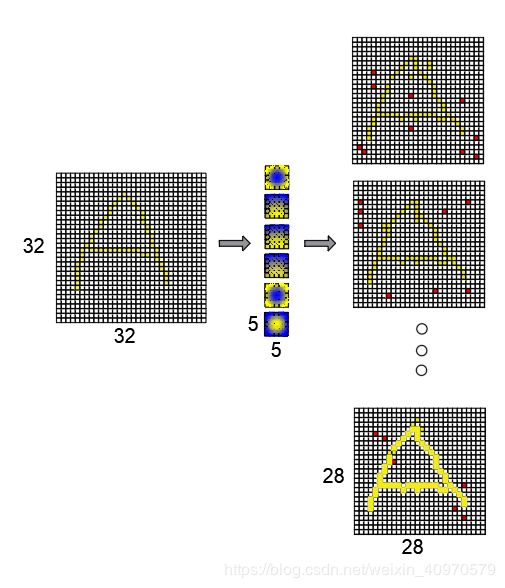
C1卷积层的过程就是图片这样,还是比较简单的,通过6个5x5的卷积核进行卷积,得到6个28x28的输出特征图。(注意,这层没有激活函数)
池化层(Subsampling,S2)
输入特征: 28 × 28 × 6
下采样区域:2 × 2
下采样方式:对2*2区域内的像素求和后,再乘以一个权值系数并加上一个偏置。
激活函数:sigmoid
下采样深度:6
输出featureMap大小:14 × 14 × 6
神经元数量:14 × 14 × 6
连接数:5880
下面对这些数字的由来进行详细的说明。
这里需要的关注的有以下几点:
- 是下采样的方式,并不是我们熟悉的平均池化核最大池化,但原理和平均池化也差不多,这里注意一下就可以了。
- 激活函数的位置,这个激活函数是放在了池化层后面,(如果想到自己搭建神经网络的话,我还是推荐放在卷积层之后,并且激活函数最好选择ReLu激活函数,这样搭配实测效果不错)。
- 池化层的大小其实也不一定非得是2x2大小的,你可以是3x3的,4x4的。
首先是池化后的输出尺寸计算:
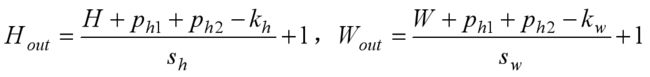
与卷积核类似,池化窗口在图片上滑动时,每次移动的步长称为步幅,当宽和高方向的移动大小不一样时,分别用sh和sw表示。也可以对需要进行池化的图片进行填充,填充方式与卷积类似,假设在第一行之前填充ph1行,在最后一行后面填充ph2行。在第一列之前填充pw1列,在最后一列之后填充pw2列,则池化层的输出特征图大小为:
(28+0+0-2)/2 +1=14。
然后是激活函数sigmoid,

就是这样的一个数学表达式,看看他的函数图像
激活函数不改变特征图的尺寸(不高,现在这个激活函数应用的比较少了),其余的参数和卷积层计算方式一样。到这里,池化层S2就说的差不多了。不过,笔者认为,池化层相当于另一种方式的激活函数,只不过这个‘激活函数’会大大降低特征图的尺寸。有的时候还会去除掉该有的特征,因此,现在有学者考虑通过控制卷积步长来代替池化层。接下来看一张图片,

红色像素点表示卷积之后出现的负值。
卷积层(Convolutions,C3)
输入特征:S2中所有6个或者几个特征map组合
卷积核大小:5 x 5
卷积核个数:16
输出featureMap大小:10 x 10 x 16
可训练参数:1516
连接数:10 x 10 x 1516 = 151600
这一层卷积说道就有点多了,按照正常的卷积原理,要想得到10 x 10 x 16的特征图,应该需要16个5 x 5 x 6形状的卷积核,但是文中卷积核并没有深度,那么它是如何实现的呢?
是通过对S2 的特征图特殊组合计算得到的16个特征图。具体如下:

这个图看的有点蒙,说的实在一点,就是将S2中的特征图进行分类,分类要求:
1)3个相连着的分成一类,6个特征图可以数出来6个不一样的;
2)4个相连着的分成一类,6个特征图可以数出来6个不一样的;
3)4个相连数不超过两个的分为一类,6个特征图可以数出来3个不一样的;
4)6个相连的分为一类,6个特征图可以数出来1个;
这样输出特征图深度就为:(6+6+3+1)=16。卷积核大小依然为55,所以总共有6(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516个参数。而图像大小为10*10,所以共有151600个连接。根据个人理解,绘制了一张图,请看。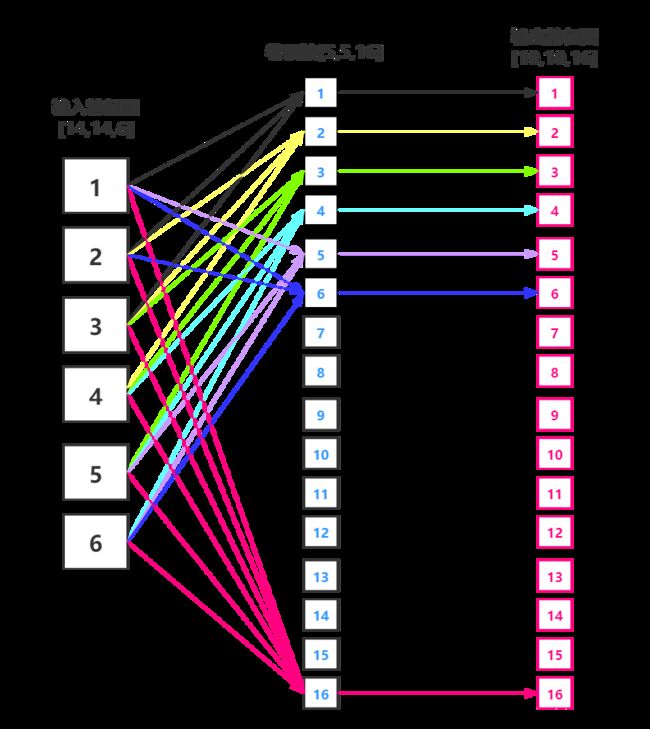
这里介绍了1)和4)卷积流程,卷积方式还是我们熟悉的先相乘再累加。这样就很清晰明了了。至于作者为什么这么连接,他给出了如下两个原因:
1. 减少参数,
2. 这种不对称的组合连接的方式有利于提取多种组合特征。
池化层(Subsampling,S4)
输入特征: 10 × 10 × 16
下采样区域:2 × 2
下采样方式:对2*2区域内的像素求和后,再乘以一个权值系数并加上一个偏置。
激活函数:sigmoid
下采样深度:16
输出featureMap大小:5 × 5 × 16
神经元数量:5 × 5 × 16=400
连接数:2000
S4中每个特征图的大小是C3中特征图大小的1/4
这个和池化层S2原理步骤都一样,不说了就。
卷积层(Convolutions,C5)
输入:S4层的全部16个单元特征map(与s4全相连)
卷积核大小:5 x 5
卷积核个数:120
输出featureMap大小:1 x 1 x 120
可训练参数:48120
连接数:41820
这一层就是将特征图拉直的一个过程。在我的上一个‘啥是卷积神经网络(一)’中已经详细说明了其工作机制。这里就不墨迹了。这里形成120个卷积结果。每个都与上一层的16个图相连。所以共有(5x5x16+1)x120 = 48120个参数,同样有48120个连接。
需要注意的是,这里的数据量较小,可以看做是没有深度的。也就是可以看做通道数都是1。
全连接层(F6)
特征输入:120 x 1
计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,
激活函数:sigmoid函数
可训练参数:84 x (120+1)=10164
详细说明:6层是全连接层。F6层有84个节点,对应于一个7x12的比特图,-1表示白色,1表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 +1)x84=10164。ASCII编码图如下:

我感觉这一块没啥说的,大家都懂。就算了吧。还剩一个输出层,也没啥介绍的,而且里面的激活函数现在基本用不上。好了,这个随笔到此结束。