- C++ 11 Lambda表达式和min_element()与max_element()的使用_c++ lamda函数 min_element((1)
2401_84976182
程序员c语言c++学习
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上CC++开发知识点,真正体系化!由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新如果你需要这些资料,可以戳这里获取#include#include#includeusingnamespacestd;boolcmp(int
- 算法学习笔记:17.蒙特卡洛算法 ——从原理到实战,涵盖 LeetCode 与考研 408 例题
在计算机科学和数学领域,蒙特卡洛算法(MonteCarloAlgorithm)以其独特的随机抽样思想,成为解决复杂问题的有力工具。从圆周率的计算到金融风险评估,从物理模拟到人工智能,蒙特卡洛算法都发挥着不可替代的作用。本文将深入剖析蒙特卡洛算法的思想、解题思路,结合实际应用场景与Java代码实现,并融入考研408的相关考点,穿插图片辅助理解,帮助你全面掌握这一重要算法。蒙特卡洛算法的基本概念蒙特卡
- 分布式学习笔记_04_复制模型
NzuCRAS
分布式学习笔记架构后端
常见复制模型使用复制的目的在分布式系统中,数据通常需要被分布在多台机器上,主要为了达到:拓展性:数据量因读写负载巨大,一台机器无法承载,数据分散在多台机器上仍然可以有效地进行负载均衡,达到灵活的横向拓展高容错&高可用:在分布式系统中单机故障是常态,在单机故障的情况下希望整体系统仍然能够正常工作,这时候就需要数据在多台机器上做冗余,在遇到单机故障时能够让其他机器接管统一的用户体验:如果系统客户端分布
- 算法学习笔记:15.二分查找 ——从原理到实战,涵盖 LeetCode 与考研 408 例题
呆呆企鹅仔
算法学习算法学习笔记考研二分查找
在计算机科学的查找算法中,二分查找以其高效性占据着重要地位。它利用数据的有序性,通过不断缩小查找范围,将原本需要线性时间的查找过程优化为对数时间,成为处理大规模有序数据查找问题的首选算法。二分查找的基本概念二分查找(BinarySearch),又称折半查找,是一种在有序数据集合中查找特定元素的高效算法。其核心原理是:通过不断将查找范围减半,快速定位目标元素。与线性查找逐个遍历元素不同,二分查找依赖
- OKHttp3源码分析——学习笔记
Sincerity_
源码相关Okhttp源码解析读书笔记httpclientcache
文章目录1.HttpClient与HttpUrlConnection的区别2.OKHttp源码分析使用步骤:dispatcher任务调度器,(后面有详细说明)Request请求RealCallAsyncCall3.OKHttp架构分析1.异步请求线程池,Dispather2.连接池清理线程池-ConnectionPool3.缓存整理线程池DisLruCache4.Http2异步事务线程池,http
- Python学习笔记5|条件语句和循环语句
iamecho9
Python从0到1学习笔记python学习笔记
一、条件语句条件语句用于根据不同的条件执行不同的代码块。1、if语句基本语法:if布尔型语句1:代码块#语句1为True时执行的代码示例:age=int(input("请输入你的年龄:"))ifage>=18:print("你已成年")2、if-else语句如果if条件不成立,则执行else代码块:if布尔型语句1:代码块#语句1为True时执行的代码else:代码块#语句1为False时执行的代
- 5G标准学习笔记14 - CSI--RS概述
刘孬孬沉迷学习
5G学习笔记信息与通信
5G标准学习笔记14-CSI–RS概述大家好~,这里是刘孬孬,今天带着大家一起学习一下5GNR中一个非常非常重要的参考信号------------------CSI-RS信号,CSI-RS不是持续发送,UE只能在网络明确配置了CSI-RS的情况下才能使用其进行信道测量。前言对于CSI-RS,肯定还离不开前面所说的CSI(channelstateinformation),前面也讲过CSI对于MIMO
- 5G标准学习笔记06-基于AI/ML波束管理
刘孬孬沉迷学习
5G学习笔记
5G标准学习笔记06-基于AI/ML波束管理前言前面对于孬孬学习了波束管理的概述,下面要进一步来看一下传统波束管理和现在3GPP中推动的AL/ML波束管理之前的区别联系。一、传统波束管理方法流程传统BM流程主要包括以下步骤:波束扫描(BeamSweeping):gNB通过顺序发送多个窄波束(SSB或CSI-RS),覆盖整个服务区域,UE测量每个波束的信号质量(如L1-RSRP或L1-SINR)。波
- 5G标准学习笔记03- CSI 反馈增强概述
刘孬孬沉迷学习
5G笔记学习
5G标准学习笔记03-CSI反馈增强概述大家好,最近在研究AI/ML3gpp标准NR空口的有关内容,后面可能会给大家介绍一下对应的有关内容AI/ML在3GPP标准中的研究进展在AI/ML在NR空口的应用中,对应标准主要聚焦了3个case进行讨论研究分别是:CSI反馈增强;波束管理;定位精度增强;这三个内容可能比较涉及RAN1/2的具体内容,后面会基于这个进行一定的介绍。今天主要是主要介绍CSI反馈
- 学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图
宁儿数据安全
#机器学习学习笔记matplotlib
学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图一、绘制混淆矩阵热图代码解析1.1、导入必要的库importmatplotlib.pyplotaspltfromsklearn.metricsimportconfusion_matriximportseabornassnsmatplotlib.pyplot:Python中最常用的绘图库,用于创建各种图表confusion_matr
- LLaMA 学习笔记
AI算法网奇
深度学习基础人工智能深度学习
目录LLaMA模型结构:模型微调手册:推理示例:指定位置加载模型测试ok:模型下载:llama-stack下载modelscope下载LLaMA优化技术RMSNormSwiGLU激活函数旋转位置编码(RoPE)LLaMA模型结构:llama3结构详解-CSDN博客模型微调手册:大模型微调LLaMA详细指南(准备环境、数据、配置微调参数+微调过程)_llama微调-CSDN博客显存占用:FP16/B
- BOOT_KEY按键(学习笔记)
小高Baby@
学习笔记
先来让我们了解一下GPIO是什么吧,它在单片机中也有很重要的作用,接下来我们来看看吧。esp32C3是QFN32封装(一种集成电路(IC)封装类型),GPIO引脚一共有22个,从GPIO-0到GPIO-21。从理论上来说,所有的IO引脚都可以复用为任何外设功能,但有些引脚用作连接芯片内部FLASH或者外部FLASH功能时,官方不建议用作其它用途。esp32c3的GPIO,可以用作输入、输出,可以配
- 【机器学习笔记Ⅰ】9 特征缩放
巴伦是只猫
机器学习机器学习笔记人工智能
特征缩放(FeatureScaling)详解特征缩放是机器学习数据预处理的关键步骤,旨在将不同特征的数值范围统一到相近的尺度,从而加速模型训练、提升性能并避免某些特征主导模型。1.为什么需要特征缩放?(1)问题背景量纲不一致:例如:特征1:年龄(范围0-100)特征2:收入(范围0-1,000,000)梯度下降的困境:量纲大的特征(如收入)会导致梯度更新方向偏离最优路径,收敛缓慢。量纲小的特征(如
- Kotlin学习笔记
qq_26907861
1.Val和Varval:用于声明不可变量,不可变是指引用不可变;var:用于声明可变的变量;packagehello//可选的包头funmain(args:Array){//包级可见的函数,接受一个字符串数组作为参数vala="不可变的变量"//不可变的变量varn=2//可变println(a)println(n)}2.fun函数Kotlin中的函数可以这样声明:fun函数名(参数列表):返回
- WPF学习笔记(2)——x名称空间详解 上
幽冥宇少
WPFC#WPF学习笔记初学者C#VS2013
先说一些基本的,.NET的模块称为程序集(Assembly)。一般情况下,用VS创建的是解决方案(Solution),一个解决方案就是一个完整的程序。解决方案中包含若干个项目(Project),每个项目是可以独立编译的,他的编译结果是一个程序集。常见的程序集是以.exe为扩展名的可执行程序或者是以.dll为扩展名的动态链接库,大多数情况下,我们说“引用其他程序集”的时候,说的是动态链接库。因为.N
- 初学者的指针学习笔记(1)
近津薪荼
学习笔记
1.内存和地址1.1内存像学生宿舍一样,被分成许多个房间,每个房间都有自己的房号,每个房间能住8个学生内存被分成许多个单元(小为1Byte),每个单元都有自己的编号,每个单元里能住8个小比特(bite)c语言中,指针就是该单元内存的编号也就是地址,我们可以通过指针快速找到我们要访问的内存1.2编址计算机中的内存编址,是通过硬件设计来完成的,也就是说他被做出来的时候各个内存单元的地址就已经确定了。计
- 初学者关于自定义类型结构体的学习笔记
近津薪荼
学习笔记数据结构
1.结构的特殊声明//匿名结构体类型struct{inta;charb;floatc;}x;struct{inta;charb;floatc;}a[20],*p;p=&x;不可取,本质上是两个不同类型的结构体上述代码的声明方式,该结构体类型,如果不重命名的话,只能用一次(声明时顺便创建变量)2.结构体的自引用structNode{intdata;structNodenext;};上述代码,结构体中
- Xilinx系FPGA学习笔记(三)Vivado的仿真及ILA使用
贾saisai
FPGA学习fpga开发学习笔记
系列文章目录文章目录系列文章目录前言仿真验证(类似modelsim)ILA在线调试工具添加ILAILA的例化ILA的使用前言接着学习vivado的使用方法仿真验证(类似modelsim)首先类似添加.v文件的方法,在File-AddSource中选择Addorcreatesimulationsources或者直接在Sources里面选就行然后就编写testbench,类似之前介绍的modelsim
- 学习笔记day1
Linux基础Linux到底是什么?Linux主要指的是内核(主机中的CPU),它也是我们系统的大脑Ubuntu跟Linux的关系:Ubuntu是Linux系统的一个分支。为什么要选⽤Linux?开源的,用户可以根据自己的喜好和需求来定制系统。性免费,企业可以减少开发成本。安全性可移植性高Linux跟我们⽇常使⽤的windows的区别?操作习惯不⼀样:windows是以图形交互为主;Linux操作
- 【机器学习|学习笔记】用 Python 结合 graphviz 生成 ID3、C4.5、CART 三种决策树的结构示意图。
【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图文章目录【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图用Python结合graphviz生成ID3、C4.5、CART三种
- Text2Reward学习笔记
1.提示词请问,“glew”是一个RL工程师常用的工具库吗?请问,thiscodebase主要是做什么用的呀?1.1解释代码是否可以请您根据thiscodebase的主要功能,参考PyTorch的文档格式和文档风格,使用Markdown格式为选中的代码行编写一段相应的文档说明呢?2.项目环境配置2.1新建环境[official]2.1.1Featurizecondacreate-p~/work/d
- pandas学习笔记
kara_486
pandas学习笔记
pandas是python中一个性能强大的数据处理库,能进行复杂的数据处理。pandas的数据结构分为三种类型,分别为series,DataFrame和index,对于初学者而言,series和DataFrame这两种结构最为重要。下面作者将重点介绍series和DataFrame这两部分。series的介绍series按照作者的目前的理解是pandas库中最基础的组成部分,seriers是由索引
- 英语学习笔记2.0
飞升不如收破烂~
学习笔记
✅正确表达:“HowlonghaveyoubeenteachingEnglish?”或者更简单地问:“HowlongdoyouteachEnglish?”(这个句子语法对,但用在现在习惯性的行为上)用法说明:如果你想问:️“你教英语多久了?”✅用现在完成时(表示一段持续的时间):HowlonghaveyoubeenteachingEnglish?️你可以这样试试新的句子:Howlonghaveyo
- C语言笔记
学习笔记仅供参考基础介绍程序就是一组计算机能识别的指令,计算机的一切操作都是由程序控制的。人和计算机都能识别的语言就是就是计算机语言,计算机工作是基于二进制的。计算机能直接识别的二进制代码就是机器指令,机器指令的集合就是机器语言。机器语言与人们习惯使用的语言差别太大,所以人们创造出了符号语言,计算机不能直接识别符号语言的指令,需要汇编程序软件将符号语言指令转成机器指令(二进制代码)。机器语言与汇编
- 黑马程序员_学习笔记2——wpf计算器
马林雷
- WPF学习笔记(27)科学计算器
三千道应用题
C#实例WPF学习笔记wpf
科学计算器1.前端界面2.功能代码1.前端界面2.功能代码usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Text;usingSystem.Threading.Tasks;usingSystem.Windows;usingSystem.Windows.Controls;usingSystem.Wind
- 【机器学习笔记Ⅰ】10 特征工程
特征工程(FeatureEngineering)详解特征工程是机器学习和数据科学中的核心环节,旨在通过对原始数据的转换、组合和提取,构建更适合模型的高质量特征。其质量直接决定模型性能上限(“数据和特征决定了模型的上限,而算法只是逼近这个上限”)。1.特征工程的核心目标提升模型性能:增强特征与目标变量的相关性。降低计算成本:减少冗余特征,加速训练。改善泛化能力:避免过拟合,提高鲁棒性。2.特征工程的
- Java基础学习笔记2
qichi333
学习笔记javaeclipse
今天是Java基础学习第二天,加油!!!下面是我今天记的一些笔记。(有点懒惰了,爬虫今天没学,因为赖床了(bushi),但我会勤奋起来的^_^,一定一定!明天不能偷懒了天!!)一、运算符例子:inta=10;intb=20;intc=a+b;其中,“+”是运算符,且是算术运算符;“a+b”是表达式,且是算术表达式。1.算术运算符例1:publicclassdemo3{publicstaticvoi
- SystemVerilog LRM 学习笔记 -- clocking块
1clocking...endclocking块clocking块是SV新feature,主要是为了更好解决testbench和DUT之间的timing和同步建模的问题,可以使user基于clockcycle在更高的抽象层次上写testbench(如“##3”,表示三个clock)。clocking只能在module/interface/checker/program中声明,不能在function
- JavaWeb(苍穹外卖)--学习笔记03(登录生成令牌)
老虎0627
JavaWeb(苍穹外卖)学习笔记java
前言本片文章是学习B站黑马程序员苍穹外卖的学习笔记。在Day01(如果学到登录界面这里卡住了,可以看看这篇文章),登陆界面的后端实现大致可以分为两部分登录功能和登录校验,其中登陆校验的实现是基于令牌JWT技术来实现会话追踪(校验部分还有拦截器Interceptor这个我没太学懂视频也没提,以后在更)JWT令牌基本概念JWT是一种在Web应用程序,简单且安全地处理用户身份验证和信息交换的技术,首先我
- JAVA基础
灵静志远
位运算加载Date字符串池覆盖
一、类的初始化顺序
1 (静态变量,静态代码块)-->(变量,初始化块)--> 构造器
同一括号里的,根据它们在程序中的顺序来决定。上面所述是同一类中。如果是继承的情况,那就在父类到子类交替初始化。
二、String
1 String a = "abc";
JAVA虚拟机首先在字符串池中查找是否已经存在了值为"abc"的对象,根
- keepalived实现redis主从高可用
bylijinnan
redis
方案说明
两台机器(称为A和B),以统一的VIP对外提供服务
1.正常情况下,A和B都启动,B会把A的数据同步过来(B is slave of A)
2.当A挂了后,VIP漂移到B;B的keepalived 通知redis 执行:slaveof no one,由B提供服务
3.当A起来后,VIP不切换,仍在B上面;而A的keepalived 通知redis 执行slaveof B,开始
- java文件操作大全
0624chenhong
java
最近在博客园看到一篇比较全面的文件操作文章,转过来留着。
http://www.cnblogs.com/zhuocheng/archive/2011/12/12/2285290.html
转自http://blog.sina.com.cn/s/blog_4a9f789a0100ik3p.html
一.获得控制台用户输入的信息
&nbs
- android学习任务
不懂事的小屁孩
工作
任务
完成情况 搞清楚带箭头的pupupwindows和不带的使用 已完成 熟练使用pupupwindows和alertdialog,并搞清楚两者的区别 已完成 熟练使用android的线程handler,并敲示例代码 进行中 了解游戏2048的流程,并完成其代码工作 进行中-差几个actionbar 研究一下android的动画效果,写一个实例 已完成 复习fragem
- zoom.js
换个号韩国红果果
oom
它的基于bootstrap 的
https://raw.github.com/twbs/bootstrap/master/js/transition.js transition.js模块引用顺序
<link rel="stylesheet" href="style/zoom.css">
<script src=&q
- 详解Oracle云操作系统Solaris 11.2
蓝儿唯美
Solaris
当Oracle发布Solaris 11时,它将自己的操作系统称为第一个面向云的操作系统。Oracle在发布Solaris 11.2时继续它以云为中心的基调。但是,这些说法没有告诉我们为什么Solaris是配得上云的。幸好,我们不需要等太久。Solaris11.2有4个重要的技术可以在一个有效的云实现中发挥重要作用:OpenStack、内核域、统一存档(UA)和弹性虚拟交换(EVS)。
- spring学习——springmvc(一)
a-john
springMVC
Spring MVC基于模型-视图-控制器(Model-View-Controller,MVC)实现,能够帮助我们构建像Spring框架那样灵活和松耦合的Web应用程序。
1,跟踪Spring MVC的请求
请求的第一站是Spring的DispatcherServlet。与大多数基于Java的Web框架一样,Spring MVC所有的请求都会通过一个前端控制器Servlet。前
- hdu4342 History repeat itself-------多校联合五
aijuans
数论
水题就不多说什么了。
#include<iostream>#include<cstdlib>#include<stdio.h>#define ll __int64using namespace std;int main(){ int t; ll n; scanf("%d",&t); while(t--)
- EJB和javabean的区别
asia007
beanejb
EJB不是一般的JavaBean,EJB是企业级JavaBean,EJB一共分为3种,实体Bean,消息Bean,会话Bean,书写EJB是需要遵循一定的规范的,具体规范你可以参考相关的资料.另外,要运行EJB,你需要相应的EJB容器,比如Weblogic,Jboss等,而JavaBean不需要,只需要安装Tomcat就可以了
1.EJB用于服务端应用开发, 而JavaBeans
- Struts的action和Result总结
百合不是茶
strutsAction配置Result配置
一:Action的配置详解:
下面是一个Struts中一个空的Struts.xml的配置文件
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE struts PUBLIC
&quo
- 如何带好自已的团队
bijian1013
项目管理团队管理团队
在网上看到博客"
怎么才能让团队成员好好干活"的评论,觉得写的比较好。 原文如下: 我做团队管理有几年了吧,我和你分享一下我认为带好团队的几点:
1.诚信
对团队内成员,无论是技术研究、交流、问题探讨,要尽可能的保持一种诚信的态度,用心去做好,你的团队会感觉得到。 2.努力提
- Java代码混淆工具
sunjing
ProGuard
Open Source Obfuscators
ProGuard
http://java-source.net/open-source/obfuscators/proguardProGuard is a free Java class file shrinker and obfuscator. It can detect and remove unused classes, fields, m
- 【Redis三】基于Redis sentinel的自动failover主从复制
bit1129
redis
在第二篇中使用2.8.17搭建了主从复制,但是它存在Master单点问题,为了解决这个问题,Redis从2.6开始引入sentinel,用于监控和管理Redis的主从复制环境,进行自动failover,即Master挂了后,sentinel自动从从服务器选出一个Master使主从复制集群仍然可以工作,如果Master醒来再次加入集群,只能以从服务器的形式工作。
什么是Sentine
- 使用代理实现Hibernate Dao层自动事务
白糖_
DAOspringAOP框架Hibernate
都说spring利用AOP实现自动事务处理机制非常好,但在只有hibernate这个框架情况下,我们开启session、管理事务就往往很麻烦。
public void save(Object obj){
Session session = this.getSession();
Transaction tran = session.beginTransaction();
try
- maven3实战读书笔记
braveCS
maven3
Maven简介
是什么?
Is a software project management and comprehension tool.项目管理工具
是基于POM概念(工程对象模型)
[设计重复、编码重复、文档重复、构建重复,maven最大化消除了构建的重复]
[与XP:简单、交流与反馈;测试驱动开发、十分钟构建、持续集成、富有信息的工作区]
功能:
- 编程之美-子数组的最大乘积
bylijinnan
编程之美
public class MaxProduct {
/**
* 编程之美 子数组的最大乘积
* 题目: 给定一个长度为N的整数数组,只允许使用乘法,不能用除法,计算任意N-1个数的组合中乘积中最大的一组,并写出算法的时间复杂度。
* 以下程序对应书上两种方法,求得“乘积中最大的一组”的乘积——都是有溢出的可能的。
* 但按题目的意思,是要求得这个子数组,而不
- 读书笔记-2
chengxuyuancsdn
读书笔记
1、反射
2、oracle年-月-日 时-分-秒
3、oracle创建有参、无参函数
4、oracle行转列
5、Struts2拦截器
6、Filter过滤器(web.xml)
1、反射
(1)检查类的结构
在java.lang.reflect包里有3个类Field,Method,Constructor分别用于描述类的域、方法和构造器。
2、oracle年月日时分秒
s
- [求学与房地产]慎重选择IT培训学校
comsci
it
关于培训学校的教学和教师的问题,我们就不讨论了,我主要关心的是这个问题
培训学校的教学楼和宿舍的环境和稳定性问题
我们大家都知道,房子是一个比较昂贵的东西,特别是那种能够当教室的房子...
&nb
- RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系
daizj
oraclermanfilespersetPARALLELISM
RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系 转
PARALLELISM ---
我们还可以通过parallelism参数来指定同时"自动"创建多少个通道:
RMAN > configure device type disk parallelism 3 ;
表示启动三个通道,可以加快备份恢复的速度。
- 简单排序:冒泡排序
dieslrae
冒泡排序
public void bubbleSort(int[] array){
for(int i=1;i<array.length;i++){
for(int k=0;k<array.length-i;k++){
if(array[k] > array[k+1]){
- 初二上学期难记单词三
dcj3sjt126com
sciet
concert 音乐会
tonight 今晚
famous 有名的;著名的
song 歌曲
thousand 千
accident 事故;灾难
careless 粗心的,大意的
break 折断;断裂;破碎
heart 心(脏)
happen 偶尔发生,碰巧
tourist 旅游者;观光者
science (自然)科学
marry 结婚
subject 题目;
- I.安装Memcahce 1. 安装依赖包libevent Memcache需要安装libevent,所以安装前可能需要执行 Shell代码 收藏代码
dcj3sjt126com
redis
wget http://download.redis.io/redis-stable.tar.gz
tar xvzf redis-stable.tar.gz
cd redis-stable
make
前面3步应该没有问题,主要的问题是执行make的时候,出现了异常。
异常一:
make[2]: cc: Command not found
异常原因:没有安装g
- 并发容器
shuizhaosi888
并发容器
通过并发容器来改善同步容器的性能,同步容器将所有对容器状态的访问都串行化,来实现线程安全,这种方式严重降低并发性,当多个线程访问时,吞吐量严重降低。
并发容器ConcurrentHashMap
替代同步基于散列的Map,通过Lock控制。
&nb
- Spring Security(12)——Remember-Me功能
234390216
Spring SecurityRemember Me记住我
Remember-Me功能
目录
1.1 概述
1.2 基于简单加密token的方法
1.3 基于持久化token的方法
1.4 Remember-Me相关接口和实现
- 位运算
焦志广
位运算
一、位运算符C语言提供了六种位运算符:
& 按位与
| 按位或
^ 按位异或
~ 取反
<< 左移
>> 右移
1. 按位与运算 按位与运算符"&"是双目运算符。其功能是参与运算的两数各对应的二进位相与。只有对应的两个二进位均为1时,结果位才为1 ,否则为0。参与运算的数以补码方式出现。
例如:9&am
- nodejs 数据库连接 mongodb mysql
liguangsong
mongodbmysqlnode数据库连接
1.mysql 连接
package.json中dependencies加入
"mysql":"~2.7.0"
执行 npm install
在config 下创建文件 database.js
- java动态编译
olive6615
javaHotSpotjvm动态编译
在HotSpot虚拟机中,有两个技术是至关重要的,即动态编译(Dynamic compilation)和Profiling。
HotSpot是如何动态编译Javad的bytecode呢?Java bytecode是以解释方式被load到虚拟机的。HotSpot里有一个运行监视器,即Profile Monitor,专门监视
- Storm0.9.5的集群部署配置优化
roadrunners
优化storm.yaml
nimbus结点配置(storm.yaml)信息:
# Licensed to the Apache Software Foundation (ASF) under one
# or more contributor license agreements. See the NOTICE file
# distributed with this work for additional inf
- 101个MySQL 的调节和优化的提示
tomcat_oracle
mysql
1. 拥有足够的物理内存来把整个InnoDB文件加载到内存中——在内存中访问文件时的速度要比在硬盘中访问时快的多。 2. 不惜一切代价避免使用Swap交换分区 – 交换时是从硬盘读取的,它的速度很慢。 3. 使用电池供电的RAM(注:RAM即随机存储器)。 4. 使用高级的RAID(注:Redundant Arrays of Inexpensive Disks,即磁盘阵列
- zoj 3829 Known Notation(贪心)
阿尔萨斯
ZOJ
题目链接:zoj 3829 Known Notation
题目大意:给定一个不完整的后缀表达式,要求有2种不同操作,用尽量少的操作使得表达式完整。
解题思路:贪心,数字的个数要要保证比∗的个数多1,不够的话优先补在开头是最优的。然后遍历一遍字符串,碰到数字+1,碰到∗-1,保证数字的个数大于等1,如果不够减的话,可以和最后面的一个数字交换位置(用栈维护十分方便),因为添加和交换代价都是1
![]() ,
,![]() 表示掷硬币结果为正面朝上,
表示掷硬币结果为正面朝上,![]() 表示反面朝上。根据常识,我们都认为两种情况概率各为0.5。那么,如果遇到一个破损的硬币,将
表示反面朝上。根据常识,我们都认为两种情况概率各为0.5。那么,如果遇到一个破损的硬币,将![]() 的概率记作参数
的概率记作参数![]() ,因此:
,因此:![]() (1)
(1)![]() ,同理可知
,同理可知![]() 。这种分布(伯努利分布)的概率分布可以写成:
。这种分布(伯努利分布)的概率分布可以写成:![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() ,变量彼此都是独立同分布的,那么得到的似然函数为:
,变量彼此都是独立同分布的,那么得到的似然函数为:![]() 的导数:
的导数:![]() 的最大值:
的最大值: ![]() 个变量中变量值为1的数量。
个变量中变量值为1的数量。![]() 的思想来源于传统概率学家的观点,他们认为,参数是一个固定的值,而使得观测集合中的似然函数最大的参数值,便是最合理的参数。直观上理解,这是很有道理的,但是,在极端情况下(一般是观测样本较少的情况),利用这种方法求解出来的参数值是远远偏离实际的。例如公式(8)中,如果观测集合
的思想来源于传统概率学家的观点,他们认为,参数是一个固定的值,而使得观测集合中的似然函数最大的参数值,便是最合理的参数。直观上理解,这是很有道理的,但是,在极端情况下(一般是观测样本较少的情况),利用这种方法求解出来的参数值是远远偏离实际的。例如公式(8)中,如果观测集合![]() 中m为0(可以理解为,连续多次投掷硬币,全部是反面),那么求解出来的
中m为0(可以理解为,连续多次投掷硬币,全部是反面),那么求解出来的![]() 是0,而它的意义是掷一次硬币,硬币朝上的概率,永远不可能朝上!这是多么荒谬的结论。因此,最大似然函数求解参数的方法,在样本数量较少时,可能会出现严重的过拟合问题,这是需要注意的。由此,我们可以在建模过程中引入一些先验知识(先验分布),用于辅助模型,这种方法源于贝叶斯观点,该方法将于下面进行讨论。
是0,而它的意义是掷一次硬币,硬币朝上的概率,永远不可能朝上!这是多么荒谬的结论。因此,最大似然函数求解参数的方法,在样本数量较少时,可能会出现严重的过拟合问题,这是需要注意的。由此,我们可以在建模过程中引入一些先验知识(先验分布),用于辅助模型,这种方法源于贝叶斯观点,该方法将于下面进行讨论。![]() ,不再关注单次掷硬币的伯努利分布,而是关注
,不再关注单次掷硬币的伯努利分布,而是关注![]() 观测出现m次的概率分布,这就变成了二项分布,很容易得出,二项分布的概率分布函数为:
观测出现m次的概率分布,这就变成了二项分布,很容易得出,二项分布的概率分布函数为:![]() (9)
(9)![]() (10)
(10)![]() (11)
(11)![]() 的先验概率分布
的先验概率分布![]() 。为此,我们需要找到一个形式简单的先验分布,以便推导。首先根据贝叶斯公式,说明一下先验概率分布和后验概率分布的关系:
。为此,我们需要找到一个形式简单的先验分布,以便推导。首先根据贝叶斯公式,说明一下先验概率分布和后验概率分布的关系:![]() ,而由公式(9)得知似然函数
,而由公式(9)得知似然函数![]() 的形式中带有
的形式中带有![]() 的乘积,如果先验分布也是类似的形式,根据贝叶斯公式,后验概率分布正比于先验概率分布和似然函数的乘积,那么后验概率分布的函数形式就会和先验相同了,这一性质叫做共轭性。而有一种分布可以满足这样的条件,它就是Beta分布。Beta分布的定义为:
的乘积,如果先验分布也是类似的形式,根据贝叶斯公式,后验概率分布正比于先验概率分布和似然函数的乘积,那么后验概率分布的函数形式就会和先验相同了,这一性质叫做共轭性。而有一种分布可以满足这样的条件,它就是Beta分布。Beta分布的定义为:![]() 。由于参数
。由于参数![]() 的实际意义是一个概率,因此
的实际意义是一个概率,因此![]() ,所以需要Beta分布在0-1区间上的积分是1,而经过验证,Beta分布确实满足这一点。公式(13)中的a和b是超参数,用来控制参数
,所以需要Beta分布在0-1区间上的积分是1,而经过验证,Beta分布确实满足这一点。公式(13)中的a和b是超参数,用来控制参数![]() 的分布,而不同的超参数组合对应的Beta分布图像各有差异,如下面所示:
的分布,而不同的超参数组合对应的Beta分布图像各有差异,如下面所示:![]() (16)
(16)![]() 次之后,观察到m次
次之后,观察到m次![]() ,l次
,l次![]() ,后验概率分布进行的相对应的改进。这样直观地感受到了经过
,后验概率分布进行的相对应的改进。这样直观地感受到了经过![]() 次观测之后,模型参数所得到的优化结果。而且由此也可以证明出,顺序学习的方法可以成立,数据不需要同时都用于训练模型,而是可以被分为若干个小部分,按顺序进行学习。在进行完一批训练之后,这一次得到的后验概率分布可以作为下一次的先验概率分布继续传递。同时,模型还能在观测完所有数据之前,就有预测数据分布的能力。假设模型已经观测的集合为
次观测之后,模型参数所得到的优化结果。而且由此也可以证明出,顺序学习的方法可以成立,数据不需要同时都用于训练模型,而是可以被分为若干个小部分,按顺序进行学习。在进行完一批训练之后,这一次得到的后验概率分布可以作为下一次的先验概率分布继续传递。同时,模型还能在观测完所有数据之前,就有预测数据分布的能力。假设模型已经观测的集合为![]() ,里面包括m次观察到
,里面包括m次观察到![]() ,l次
,l次![]() 。则此时模型可以做出的预测分布为(利用乘积规则):
。则此时模型可以做出的预测分布为(利用乘积规则):![]() 是服从伯努利分布的(因为只是单独一次观测),因此,所以,上式可以继续化简为:
是服从伯努利分布的(因为只是单独一次观测),因此,所以,上式可以继续化简为:![]() 的数学期望,而由公式(17)可以求解出其Beta分布的数学期望:
的数学期望,而由公式(17)可以求解出其Beta分布的数学期望:![]() 做出的预测结果。而此时,如果让模型观测到总数量(m+l)趋近于无穷大,那么公式(20)中的值会趋近于
做出的预测结果。而此时,如果让模型观测到总数量(m+l)趋近于无穷大,那么公式(20)中的值会趋近于![]() ,也就是会变成公式(8)那样。换句话说,当样本数量接近于无穷大时,贝叶斯观点和概率学家观点得到的结果是一样的!而当样本规模有限时,贝叶斯观点得到的结果总是位于先验概率和最大似然估计的结果之间,一定程度上能缓解最大似然估计在样本稀少时严重的过拟合问题。
,也就是会变成公式(8)那样。换句话说,当样本数量接近于无穷大时,贝叶斯观点和概率学家观点得到的结果是一样的!而当样本规模有限时,贝叶斯观点得到的结果总是位于先验概率和最大似然估计的结果之间,一定程度上能缓解最大似然估计在样本稀少时严重的过拟合问题。
![\large \mathrm{ln}p\(\mathcal{D}|\mu\)=\sum_{i=1}^N\mathrm{ln}p\(x_i|\mu\)=\sum_{i=1}^N\[(1-x_i\)\cdot\mathrm{ln}\(1-\mu\)+x_i\cdot\mathrm{ln}\(\mu\)]](http://img.e-com-net.com/image/info8/13406ec14f2e4e33b4a2bf487f7853ff.gif)
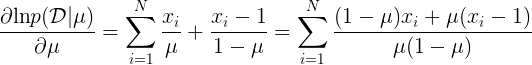
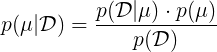


![\large \mathrm{var}[\mu]=\frac{ab}{(a+b)^2(a+b+1))}](http://img.e-com-net.com/image/info8/661cedb51ac74395a6b2d8d005f73c0d.gif)


