数学建模 of python(最短路问题)
吉吉:
Dijkstra_Animation.gif - 无向图,正权值路径
-
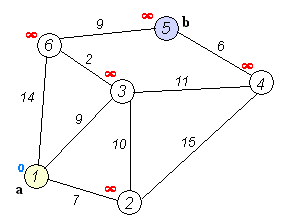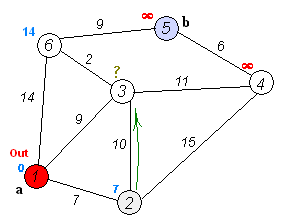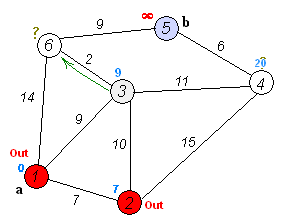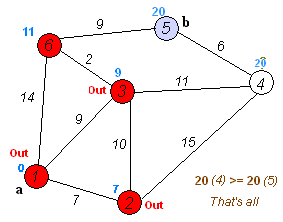
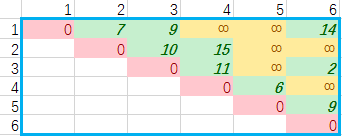
顶点为城市,顶点间连线表示城市相连通,线上数字为城市间距离。
城市间距离
-
目标为找出从序号为1的城市到序号为5的城市的最短路径。
-
该路径可以由 已知最短路径 迭代求出。
-
每次从已知最短路径中选出没探索过且最短的,从该路径终点出发,探索新的最短路径。
-
一开始,从出发点到达它之外的所有顶点的已知最短路径为无穷大,到出发点自己的最短路径为0。
-
现在,出发点的已知最短路径最小,则从出发点出发,探索与其直连的所有顶点,如果路径长度比到该顶点的已知最短路径小,则刷新该顶点的已知最短路径。
-
接着,出发点已经探索过了,从未出发探索过的已知最短路径中选出最小的一个,即从城市2出发,探索与其直连的城市,如果到达该城市的路径长度比已知最短路径小,则刷新最短路径。可以看到,从城市2到3的路径总长17>城市3目前的最短路径9,不满足条件,不刷新城市3的最短路径,而到城市4的已知最短路径刷新为7+15=21。(已知最短路径的计算都是从出发点开始)
-
依次类推,直到我们遇到目的地是已知最短路径里未探索的所有顶点中最短的一个时,终止探索。
-
值得注意的是,我们每一步探索过程中的当前出发点的最短路径是确定的了,不会再变了,因为它是所有未探索过的已知最短路径中的最小的了,所以不存在从其它地方再加一段路程到达它还会比它更小的情况。
代码(这里用到python的堆结构):
from heapq import heappop, heappush
V = [ # 顶点列表
1, 2, 3, 4, 5, 6]
w = [ # 城市间距离, -1表示无穷大
[ 0, 7, 9, -1, -1, 14],
[ 7, 0, 10, 15, -1, -1],
[ 9, 10, 0, 11, -1, 2],
[-1, 15, 11, 0, 6, -1],
[-1, -1, -1, 6, 0, 9],
[14, -1, 2, -1, 9, 0]]
def Dijkstra(V=V, w=w, s=1, dest=5):
N = len(V) # 顶点数
S = set()
Q = [(0, V.index(s), str(s))] # 路径长, 序号, 路径
v_d = V.index(dest)
while Q : # 当Q非空
d, u, p = heappop(Q)
if u == v_d :
print(d, p)
break # 可以在找到目的地之后立即终止,也可继续查找完所有最短路径
# 如果到目的地的距离已经是当前所有距离中最短的,那不可能会有更短的,所以退出
if u not in S:
S.add(u)
v_reached_from_u = [i for i in range(N) if w[u][i] != -1] # u能到达的顶点
for v in v_reached_from_u:
if v not in S:
heappush(Q,( (d + w[u][v]), v, ''.join((p,'->',str(V[v]))) )) # 到顶点v的某条路径的距离
Dijkstra() # 20 1->3->6->5