数学建模 of python(简单逻辑回归)

源自：https://www.johnwittenauer.net/machine-learning-exercises-in-python-part-3/

在本系列的第2部分中，我们使用梯度下降完成了多元线性回归的实现，并将其应用于简单的房价数据集。在这篇文章中，我们将把目标从预测连续值（回归）转换为将结果分类为两个或更多个离散桶（分类）并将其应用于学生入学问题。假设您是大学系的管理员，并且您希望根据他们在两门考试中的成绩来确定每位申请人的入学机会。您可以使用之前申请人的历史数据作为训练集。对于每个培训示例，您都有申请人在两门考试中的分数和录取决定。要做到这一点，我们'

Logistic回归

您可能想知道 - 为什么我们在分类问题上使用“回归”算法？虽然名称似乎另有说明，但逻辑回归实际上是一种分类算法。我怀疑它是这样命名的，因为它在学习方法上与线性回归非常相似，但成本和梯度函数的表达方式不同。特别是，逻辑回归使用sigmoid或“logit”激活函数而不是线性回归中的连续输出（因此名称）。我们稍后会看到更多关于实施的内容。

首先，让我们导入并检查我们将要使用的数据集。

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt  
%matplotlib inline

import os  
path = os.getcwd() + '\data\ex2data1.txt'  
data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])  
data.head()  

Exam 1	Exam 2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

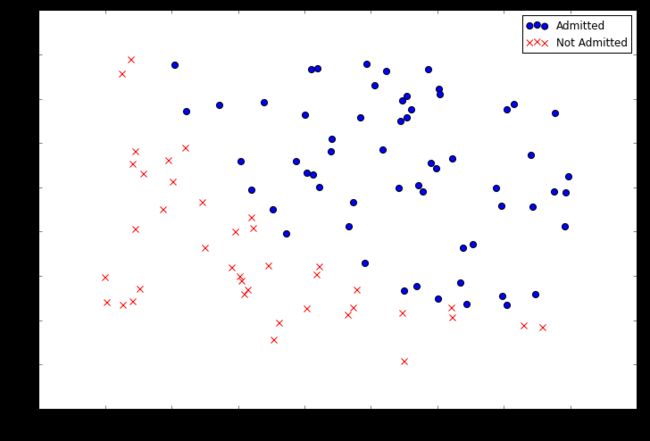
数据中有两个连续的自变量 - “考试1”和“考试2”。我们的预测目标是“Admitted”标签，它是二进制值。值为1表示学生被录取，值为0表示学生未被录取。让我们用两个分数的散点图以图形方式看这个，并使用颜色编码来可视化示例是正面还是负面。

positive = data[data['Admitted'].isin([1])]  
negative = data[data['Admitted'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')  
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')  
ax.legend()  
ax.set_xlabel('Exam 1 Score')  
ax.set_ylabel('Exam 2 Score')  

从这个图中我们可以看出，有一个近似线性的决策边界。它有点曲线所以我们不能使用直线正确地对所有例子进行分类，但我们应该能够非常接近。现在我们需要实现逻辑回归，这样我们就可以训练模型来找到最优决策边界并进行类预测。第一步是实现sigmoid函数。

def sigmoid(z):  
    return 1 / (1 + np.exp(-z))

此函数是逻辑回归输出的“激活”函数。它将连续输入转换为0到1之间的值。该值可以被解释为类概率，或者输入示例应该被正分类的可能性。使用该概率和阈值，我们可以获得离散标签预测。它有助于可视化函数的输出，以查看它真正在做什么。

nums = np.arange(-10, 10, step=1)

fig, ax = plt.subplots(figsize=(12,8))  
ax.plot(nums, sigmoid(nums), 'r')  

我们的下一步是编写成本函数。请记住，在给定一组模型参数的情况下，成本函数会评估模型在训练数据上的性能。这是逻辑回归的成本函数。

def cost(theta, X, y):  
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))

请注意，我们将输出降低到单个标量值，这是作为模型分配的类概率与示例的真实标签之间差异的函数量化的“误差”的总和。实现是完全矢量化的 - 它在一个语句（sigmoid（X * theta.T））中计算模型对整个数据集的预测。如果这里的数学没有意义，请参阅我上面链接的练习文本以获得更详细的解释。

# add a ones column - this makes the matrix multiplication work out easier
data.insert(0, 'Ones', 1)

# set X (training data) and y (target variable)
cols = data.shape[1]  
X = data.iloc[:,0:cols-1]  
y = data.iloc[:,cols-1:cols]

# convert to numpy arrays and initalize the parameter array theta
X = np.array(X.values)  
y = np.array(y.values)  
theta = np.zeros(3)

我们可以测试成本函数以确保它正常工作，但首先我们需要进行一些设置。

我喜欢经常检查我正在使用的数据结构的形状，以说服自己，他们的价值观是明智的。这种技术在实现矩阵乘法时非常有用。

X.shape, theta.shape, y.shape  

（（100L，3L），（3L，），（100L，1L））

现在让我们计算初始解决方案的成本，给出模型参数的零，这里表示为“theta”。

cost(theta, X, y)  

0.69314718055994529

现在我们有了一个工作成本函数，下一步是编写一个函数来计算模型参数的梯度，以找出如何更改参数以改善模型对训练数据的结果。回想一下，通过梯度下降，我们不仅可以随机跳动参数值，看看哪种方法效果最好。在每次训练迭代中，我们以保证将它们移动到减少训练误差的方向（即“成本”）的方式更新参数。我们可以这样做，因为成本函数是可区分的。推导该等式所涉及的微积分远远超出了本博文的范围，但完整的等式在练习文本中。这是功能。

def gradient(theta, X, y): 
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    error = sigmoid(X * theta.T) - y
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)
    return grad

请注意，我们实际上并没有在此函数中执行梯度下降 - 我们只计算一个渐变步骤。在练习中，使用名为“fminunc”的Octave函数来优化给定函数的参数，以计算成本和梯度。由于我们使用的是Python，我们可以使用SciPy的优化API来做同样的事情。

import scipy.optimize as opt 
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y)) 
cost(result[0], X, y)  

0.20357134412164668

我们现在拥有数据集的最佳模型参数。接下来，我们需要编写一个函数，使用我们学习的参数theta输出数据集X的预测。然后我们可以使用此函数来评估分类器的训练准确性。

def predict(theta, X):  
    probability = sigmoid(X * theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]
theta_min = np.matrix(result[0]) 
predictions = predict(theta_min, X)  
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)] 
accuracy = (sum(map(int, correct)) % len(correct))  
print 'accuracy = {0}%'.format(accuracy) 

准确度= 89％

我们的逻辑回归分类器正确地预测了89％的学生是否被录取。不错！请记住，这是训练集的准确性。我们没有保留保留集或使用交叉验证来获得准确度的真实近似值，因此这个数字可能高于其真实性能（本主题将在后面的练习中介绍）。

规范化Logistic回归

现在我们已经开始实现逻辑回归，我们将通过添加正则化来改进算法。正则化是成本函数中的一个术语，它使算法更喜欢“更简单”的模型（在这种情况下，模型将使用更小的系数）。该理论认为，这有助于最大限度地减少过度拟合并提高模型的推广能力。我们将逻辑回归的正则化版本应用于更具挑战性的问题。假设您是工厂的产品经理，并且您在两个不同的测试中获得了一些微芯片的测试结果。从这两个测试中，您想确定是应该接受还是拒绝微芯片。为了帮助您做出决定，您可以获得过去微芯片的测试结果数据集，

让我们从可视化数据开始。

path = os.getcwd() + '\data\ex2data2.txt'  
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
positive = data2[data2['Accepted'].isin([1])]  
negative = data2[data2['Accepted'].isin([0])]
fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')  
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')  
ax.legend() 
ax.set_xlabel('Test 1 Score')  
ax.set_ylabel('Test 2 Score')  

此数据看起来比前一个示例复杂一些。特别是，您会注意到没有线性决策边界可以很好地处理这些数据。使用逻辑回归等线性技术处理此问题的一种方法是构造从原始特征的多项式导出的特征。我们可以尝试创建一组多项式特征来输入分类器。

degree = 5  
x1 = data2['Test 1']  
x2 = data2['Test 2']
data2.insert(3, 'Ones', 1)
for i in range(1, degree):  
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)
data2.drop('Test 1', axis=1, inplace=True) 
data2.drop('Test 2', axis=1, inplace=True)
data2.head()  

	Accepted	Ones	F10	F20	F21	F30	F31	F32
0	1	1	0.051267	0.002628	0.035864	0.000135	0.001839	0.025089
1	1	1	-0.092742	0.008601	-0.063523	-0.000798	0.005891	-0.043509
2	1	1	-0.213710	0.045672	-0.147941	-0.009761	0.031616	-0.102412
3	1	1	-0.375000	0.140625	-0.188321	-0.052734	0.070620	-0.094573
4	1	1	-0.513250	0.263426	-0.238990	-0.135203	0.122661	-0.111283

现在我们需要修改成本和梯度函数以包含正则化项。在每种情况下，将正则化器添加到先前的计算中。这是更新的成本函数。

def costReg(theta, X, y, learningRate):  
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / 2 * len(X)) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / (len(X)) + reg

请注意，我们添加了一个名为“reg”的新变量，它是参数值的函数。随着参数变大，添加到成本函数的惩罚增加。另请注意，我们在函数中添加了新的“学习速率”参数。这也是等式中正则化项的一部分。学习速率为我们提供了一个新的超参数，我们可以用它来调整正则化在成本函数中的重量。

接下来，我们将向渐变函数添加正则化。

def gradientReg(theta, X, y, learningRate):  
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    error = sigmoid(X * theta.T) - y
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    return grad

与成本函数一样，正则化项被添加到原始计算中。但是，与成本函数不同，我们包含逻辑以确保第一个参数不是正则化的。这个决定背后的直觉是第一个参数被认为是模型的“偏差”或“截距”，不应该受到惩罚。

我们可以像以前一样测试新功能。

# set X and y (remember from above that we moved the label to column 0)
cols = data2.shape[1] 
X2 = data2.iloc[:,1:cols]  
y2 = data2.iloc[:,0:1]
# convert to numpy arrays and initalize the parameter array theta
X2 = np.array(X2.values) 
y2 = np.array(y2.values)  
theta2 = np.zeros(11)
learningRate = 1
costReg(theta2, X2, y2, learningRate)  

0.6931471805599454

我们还可以重复使用之前的优化代码来查找最佳模型参数。

result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))  
result2  

(array([ 0.35872309, -3.22200653, 18.97106363, -4.25297831, 18.23053189, 20.36386672, 8.94114455, -43.77439015, -17.93440473, -50.75071857, -2.84162964]), 110, 1)

theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)  
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)] 
accuracy = (sum(map(int, correct)) % len(correct))
print 'accuracy = {0}%'.format(accuracy)  

最后，我们可以使用我们之前应用的相同方法为训练数据创建标签预测并评估模型的性能。

准确度= 91％

这就是第3部分！在本系列的下一篇文章中，我们将扩展逻辑回归的实现，以解决多类图像分类问题。