划题整理,计算机应用技术——网络爬虫和深度学习
划题整理,计算机应用技术——网络爬虫和深度学习
- 1.什么是网络爬虫?
- 2.简述网络爬虫程序的执行流程?
- 3.简述使用Scrapy框架,完成一个简单的爬虫项目?
- 4.简述Scrapy框架及其工作原理?(要求画出书上的图!)
- scrapy框架
- 工作原理
- 5.简要介绍Request对象和Response对象?
- Request
- Response
- 6.如何使用Selector提取数据?
- 7.简要介绍Xpath和CSS?
- Xpath
- Xpath基础语法
- CSS
- CSS基础语法
- 8.简述如何使用Item封装数据?
- 9.简述使用ItemPipeline处理数据的过程?
- 10.简述使用LinkExtractor提取链接的过程?
- 11.给出BP反向传递学习算法中隐层到输出层权重梯度计算推导过程?
- 由链式法则有
- 从而求得
- 12.给出BP反向传递算法中输入层到隐层权重梯度计算推导过程?
- ①、由链式法则有
- ②、所以原式进一步化简
- ③、为了简化起见,将上面的式子最终表达成
- 13.使用TensorFlow实现线性回归算法?(要考程序,最好理解,注释部分可以不用写)
- 14.什么是卷积神经网络(CNN)?
- 15.对给定的CNN应用网络结构图,对各层功能及参数进行简要的描述?
- ①数据输入层
- ②卷积计算层
- ③激励层-ReLU
- ④池化层
- ⑤全连接层
1.什么是网络爬虫?
网络爬虫是指在互联网上自动爬取网站内容信息的程序,也被称作网络蜘蛛或网络机器人。大型的爬虫程序被广泛应用于搜索引擎、数据挖掘等领域,个人用户或企业也可以利用爬虫收集对自身有价值的数据。
举一个简单的例子,假设你在本地新开了一家以外卖生意为主的餐馆,现在要给菜品定价,此时便可以开发一个爬虫程序,在美团、饿了么、百度外卖这些外卖网站爬取大量其他餐馆的菜品价格作为参考,以指导定价。
2.简述网络爬虫程序的执行流程?
网络爬虫的执行流程可以总结为以下循环:
- 下载页面
网页内容的本质是HTML文本,爬取一个网页内容之前,首先要根据网页的URL下载网页 - 提取页面中的数据
当网页(HTML)下载完成后,对页面中的内容进行分析,并提取感兴趣的数据,提取数据可以多种形式保存,比如以某种格式(CSV、JSON)写入文件,或存储到数据库(MySQL、MongoDB) - 提取页面中的链接
想获取的数据往往不仅仅在一个页面中,而是分布在多个页面中,提取完当前页面数据后,提取页面中的链接,然后对链接页面进行爬取(循环1-3步)
3.简述使用Scrapy框架,完成一个简单的爬虫项目?
- 项目需求
初学者爬虫网站(http://books.toscrape.com)爬取书籍信息 - 创建项目
为了创建scrapy项目,在命令行中使用scrapy startproject命令 - 分析页面
需要对待爬取的页面进行分析,使用Chrome浏览器的开发者工具分析页面
3.1 数据信息
在网页中鼠标右键“审查元素”,查看HTML代码
3.2 链接信息
在书籍列表页面,通过点击next访问下一页,通过“审查元素”查看next的HTML代码 - 实现Spider
在scrapy中编写一个爬虫即实现一个scrapy.Spider的子类 - 运行爬虫
完成代码后在命令行中执行 scrapy crawl运行爬虫,并将爬取数据存储到csv文件
4.简述Scrapy框架及其工作原理?(要求画出书上的图!)
scrapy框架
包括Engine、Scheduler、Downloader、Spider、Middleware、ItemPipeline
工作原理
- 当爬取URL页面时,构造Request对象提交给Engine
- Request对象进入Scheduler按算法排队,之后出队送往Downloader
- Downloader根据Request中URL发送HTTP请求,利用服务器返回响应构造Response对象
- Response对象到达页面解析函数提取数据、封装Item交Engine、送往ItemPipeline处理,Exporter以某种格式写入文件
5.简要介绍Request对象和Response对象?
Request
Request对象用来描述一个HTTP请求,常用属性有:
- url 请求页面的地址
- method HTTP请求的方法
- headers HTTP请求的头部字典
- body HTTP请求的正文
- meta 元数据字典
Response
Response对象用来描述一个HTTP响应,包括三个子类:
- TextResponse
- HtmlResponse
- XmlResponse
HtmlResponse属性常用三个方法:
- xpath(query)
- css(query)
- urljoin(url)
6.如何使用Selector提取数据?
- 创建对象:可以使用HTML传递给Selector构造器的text参数,也可以使用response传递给selsector的response参数
- 选中数据:调用selector对象的xpath方法或css方法选中文档的某个部分
- 提取数据:调用Selector或SelectorLis对象的方法可以将选中内容提取
7.简要介绍Xpath和CSS?
Xpath
Xpath即XML路径语言,是用来确定xml文档中某部分位置的语言
Xpath基础语法
/ 选中文档的根
. 选中当前节点
.. 选中当前节点的父节点
ELEMENT选中子节点中所有ELEMENT元素节点
//ELEMENT选中后代节点中所有ELEMENT元素节点
*选中所有元素子节点
text()选中所有文本子节点
@ATTR选中名为ATTR的属性节点
@*选中所有属性节点
[谓语]谓语用来查找某个特定的节点或者包含某个特定值的节点
CSS
CSS即层叠样式表,选择器是一种用来确定HTML文档中某部分位置的语言,CSS选择器的语法比Xpath稍微简单一些,但功能不如Xpath强大。
CSS基础语法
*选中所有元素
E选中E元素
E1,E2选中E1和E2元素
E1 E2选中E1后代元素中的E2元素
E1>E2选中E1子元素中的E2元素
E1+E2选中E1兄弟元素中的E2元素
.CLASS选中CLASS属性包含CLASS的元素
#ID选中id属性为ID的元素
[ATTR]选中包含ATTR属性的元素
[ATTR=VALUE]选中包含ATTR属性且值为VALUE的元素
[ATTR~=VALUE]选中包含ATTR属性且值包含VALUE的元素
E:nth-child(n)或者 E:nth-last-child(n)选中E元素,且该元素必须是其父元素的(或者倒数)第n个子元素
E:first-child或者·E:last-child选中E元素,且该元素必须是其父元素的(或者倒数)第一个子元素
E:empty选中没有子元素的E元素
E::text选中E元素的文本节点(Text Node)
8.简述如何使用Item封装数据?
对于提取到的网站中的多个信息字段,最容易想到是用Python的字典来维护这些零散的信息字段。由于字典
①不够直观、②容易写错、③不便传递给其他组件,在Scrapy中可以使用自定义的Item类封装数据。
Scrapy提供了Item和Field两个类,用户可以使用他们来自定义一个数据类,从而封装数据
为了自定义数据类,只需继承Item,并创建一系列Field对象的类属性即可。
①定义好的Item支持字典接口,因此Item在使用上和字典类似,
②并且Item内部会对字段名检测,当用户赋值没有意义字段时抛出错误。
③那么接下来使用Field元数据即可传递额外信息给处理数据的某个组件,告诉组件应该以怎样的方式处理数据。
9.简述使用ItemPipeline处理数据的过程?
ItemPipeline是处理数据的组件,一个ItemPipeline就是一个包含特定接口的类,通常只负责一种功能的数据处理,在一个项目中可以同时启用多个ItemPipeline,他们按指定次序级联起来,形成一条数据处理流水线。
ItemPipeline的几种典型应用
- 清洗数据
- 验证数据的有效性
- 过滤掉重复的数据
- 将数据存入数据库
在创建一个Scrapy项目时,会自动生成一个pipelines.py文件,它用来放置用户自定义的ItemPipeline,在其中可以按需求选择各种常用的方法。
在Scrapy中,ItemPipeline是可选的组件,想要启用某个(或某些)ItemPipeline需要在配置文件settings.py中进行配置即可使用。
10.简述使用LinkExtractor提取链接的过程?
Scrapy提供了一个专门用于提取链接的类LinkExtractor,在提取大量链接或提取规则比较复杂时,使用LinkExtractor更加方便。
使用LinkExtractor对象提取页面中链接的流程如下:
- 导入LinkExtractor,它位于scrapy.linkextractors模块
- 创建一个LinkExtractor对象使用一个或多个构造器参数描述提取规则
- 调用LinkExtractor对象的extract_links方法传入一个Response对象,该方法依据创建对象时所描述的提取规则,在Response对象所包含的页面中提取链接,最终返回一个列表,其中的每一个元素都是一个Link对象,即提取到的一个链接
- 由于页面中的下一页链接只有一个,因此用links[0]获取Link对象,Link对象的url属性便是链接页面的绝对url地址(无须再调用 response.urljoin方法),用其构造Request对象并提交。
11.给出BP反向传递学习算法中隐层到输出层权重梯度计算推导过程?
隐层到输出层权重梯度计算:
由链式法则有
∂ ε k ∂ w h j k = ∂ ε k ∂ s ( y j k ) ∂ S ( y j k ) ∂ y j k ∂ y j k ∂ w h j k \frac{\partial \varepsilon_{k}}{\partial w_{h j}^{k}}=\frac{\partial \varepsilon_{k}}{\partial s\left(y_{j}^{k}\right)} \frac{\partial \mathcal{S}\left(y_{j}^{k}\right)}{\partial y_{j}^{k}} \frac{\partial y_{j}^{k}}{\partial w_{h j}^{k}} ∂whjk∂εk=∂s(yjk)∂εk∂yjk∂S(yjk)∂whjk∂yjk那么其中
∂ ε k ∂ s ( y j k ) = − ( d j k − S ( y j k ) ) = − e j k \frac{\partial \varepsilon_{k}}{\partial s\left(y_{j}^{k}\right)}=-\left(d_{j}^{k}-\mathcal{S}\left(y_{j}^{k}\right)\right)=-e_{j}^{k} ∂s(yjk)∂εk=−(djk−S(yjk))=−ejk
∂ s ( y j k ) ∂ y j k = S ′ ( y j k ) = S ( y j k ) ( 1 − S ( y j k ) ) \frac{\partial s\left(y_{j}^{k}\right)}{\partial y_{j}^{k}}=\mathcal{S}^{\prime}\left(y_{j}^{k}\right)=\mathcal{S}\left(y_{j}^{k}\right)\left(1-\mathcal{S}\left(y_{j}^{k}\right)\right) ∂yjk∂s(yjk)=S′(yjk)=S(yjk)(1−S(yjk))
∂ y j k ∂ w h j k = S ( z h k ) \frac{\partial y_{j}^{k}}{\partial w_{h j}^{k}}=\mathcal{S}\left(z_{h}^{k}\right) ∂whjk∂yjk=S(zhk)
从而求得
∂ ε k ∂ w n j k = − e j k S ′ ( y j k ) S ( z h k ) = − δ j k S ( z h k ) \frac{\partial \varepsilon_{k}}{\partial w_{n j}^{k}}=-e_{j}^{k} \mathcal{S}^{\prime}\left(y_{j}^{k}\right) \mathcal{S}\left(z_{h}^{k}\right)=-\delta_{j}^{k} \mathcal{S}\left(z_{h}^{k}\right) ∂wnjk∂εk=−ejkS′(yjk)S(zhk)=−δjkS(zhk)为了简化起见,令
δ j k = e j k S ′ ( y j k ) \delta_{j}^{k}=e_{j}^{k} \mathcal{S}^{\prime}\left(y_{j}^{k}\right) δjk=ejkS′(yjk)
12.给出BP反向传递算法中输入层到隐层权重梯度计算推导过程?
输入层到隐层权重梯度计算:
①、由链式法则有
∂ ε k ∂ w i h k = ∂ ε k ∂ S ( z h k ) δ ( z h k ) ∂ z h k ∂ z h k ∂ w i h k \frac{\partial \varepsilon_{k}}{\partial w_{i h}^{k}}=\frac{\partial \varepsilon_{k}}{\partial \mathcal{S}\left(z_{h}^{k}\right)} \frac{\delta\left(z_{h}^{k}\right)}{\partial z_{h}^{k}} \frac{\partial z_{h}^{k}}{\partial w_{i h}^{k}} ∂wihk∂εk=∂S(zhk)∂εk∂zhkδ(zhk)∂wihk∂zhk
并且其中的
∂ ε k ∂ s ( z h k ) = ∑ j = 1 p { ∂ ε k ∂ y j k ∂ y j k ∂ s ( z h k ) } \frac{\partial \varepsilon_{k}}{\partial s\left(z_{h}^{k}\right)}=\sum_{j=1}^{p}\left\{\frac{\partial \varepsilon_{k}}{\partial y_{j}^{k}} \frac{\partial y_{j}^{k}}{\partial s\left(z_{h}^{k}\right)}\right\} ∂s(zhk)∂εk=j=1∑p{∂yjk∂εk∂s(zhk)∂yjk}
有了上面的基础之后,再重新推导
∂ ε k ∂ w i h k = ∑ j = 1 p { ∂ ε k ∂ y j k ∂ y j k ∂ s ( z h k ) } S ′ ( z h k ) S ( x i k ) \frac{\partial \varepsilon_{k}}{\partial w_{i h}^{k}}=\sum_{j=1}^{p}\left\{\frac{\partial \varepsilon_{k}}{\partial y_{j}^{k}} \frac{\partial y_{j}^{k}}{\partial s\left(z_{h}^{k}\right)}\right\} \mathcal{S}^{\prime}\left(z_{h}^{k}\right) \mathcal{S}\left(x_{i}^{k}\right) ∂wihk∂εk=j=1∑p{∂yjk∂εk∂s(zhk)∂yjk}S′(zhk)S(xik)
= ∑ j = 1 p { ∂ ε k ∂ s ( y j k ) ∂ s ( y j k ) ∂ y j k ∂ y j k ∂ s ( z ℏ k ) } S ′ ( z h k ) s ( x i k ) =\sum_{j=1}^{p}\left\{\frac{\partial \varepsilon_{k}}{\partial s\left(y_{j}^{k}\right)} \frac{\partial s\left(y_{j}^{k}\right)}{\partial y_{j}^{k}} \frac{\partial y_{j}^{k}}{\partial s\left(z_{\hbar}^{k}\right)}\right\} \mathcal{S}^{\prime}\left(z_{h}^{k}\right) s\left(x_{i}^{k}\right) =j=1∑p{∂s(yjk)∂εk∂yjk∂s(yjk)∂s(zℏk)∂yjk}S′(zhk)s(xik)
又因为对于上式中偏导数已知
∂ ε k ∂ s ( y j k ) = − ( d j k − S ( y j k ) ) = − e j k \frac{\partial \varepsilon_{k}}{\partial s\left(y_{j}^{k}\right)}=-\left(d_{j}^{k}-\mathcal{S}\left(y_{j}^{k}\right)\right)=-e_{j}^{k} ∂s(yjk)∂εk=−(djk−S(yjk))=−ejk
∂ s ( y j k ) ∂ y j k = S ′ ( y j k ) \frac{\partial s\left(y_{j}^{k}\right)}{\partial y_{j}^{k}}=\mathcal{S}^{\prime}\left(y_{j}^{k}\right) ∂yjk∂s(yjk)=S′(yjk)
y j k = ∑ i = 0 q w h j k S ( z h k ) , j = 1 , … , p y_{j}^{k}=\sum_{i=0}^{q} w_{h j}^{k} \mathcal{S}\left(z_{h}^{k}\right), j=1, \dots, p yjk=i=0∑qwhjkS(zhk),j=1,…,p
②、所以原式进一步化简
∂ ε k ∂ w i h k = ∑ j = 1 p { − e j k S ′ ( y j k ) w h j k } S ′ ( z h k ) x i k \frac{\partial \varepsilon_{k}}{\partial w_{i h}^{k}}=\sum_{j=1}^{p}\left\{-e_{j}^{k} \mathcal{S}^{\prime}\left(y_{j}^{k}\right) w_{h j}^{k}\right\} \mathcal{S}^{\prime}\left(z_{h}^{k}\right) x_{i}^{k} ∂wihk∂εk=j=1∑p{−ejkS′(yjk)whjk}S′(zhk)xik
= − ∑ j = 1 p { δ j k w h j k } S ′ ( z h k ) x i k =-\sum_{j=1}^{p}\left\{\delta_{j}^{k} w_{h j}^{k}\right\} \mathcal{S}^{\prime}\left(z_{h}^{k}\right) x_{i}^{k} =−j=1∑p{δjkwhjk}S′(zhk)xik
③、为了简化起见,将上面的式子最终表达成
∂ ε k ∂ w i h k = − δ h k x i k \frac{\partial \varepsilon_{k}}{\partial w_{i h}^{k}}=-\delta_{h}^{k} x_{i}^{k} ∂wihk∂εk=−δhkxik
其中
δ h k = e h k S ′ ( z h k ) \delta_{h}^{k}=e_{h}^{k} \mathcal{S}^{\prime}\left(z_{h}^{k}\right) δhk=ehkS′(zhk)
再对其中化简
e h k = ∑ j = 1 p δ j k w h j k e_{h}^{k}=\sum_{j=1}^{p} \delta_{j}^{k} w_{h j}^{k} ehk=j=1∑pδjkwhjk
13.使用TensorFlow实现线性回归算法?(要考程序,最好理解,注释部分可以不用写)
import tensorflow as tf
import numpy as np
x_data = np.float32(np.random.rand(2, 100))
y_data = np.dot([0.100, 0.200], x_data) + 0.300
b = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.random_uniform([1, 2], -1.0, 1.0))
y = tf.matmul(W, x_data) + b
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
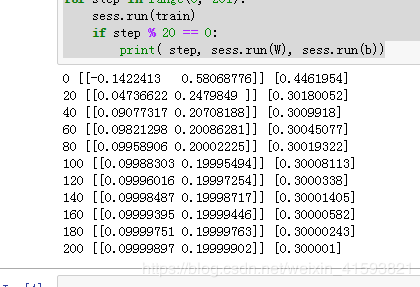
for step in range(0, 201):
sess.run(train)
if step % 20 == 0:
print( step, sess.run(W), sess.run(b))
14.什么是卷积神经网络(CNN)?
卷积神经网络是一种前馈神经网络,卷积神经网络是受生物学上感受野的机制提出的。一个神经元的感受野是指特定区域,只有这个区域内的刺激才能够激活该神经元,包括局部连接、权值共享、采样,具有平移、缩放和扭曲不变性
15.对给定的CNN应用网络结构图,对各层功能及参数进行简要的描述?
①数据输入层
- 去均值:把输入数据各个维度都中心化到0。
- 归一化:幅度归一化到同样的范围。
- PCA/白化:用PCA降维,白化是对数据每个特征轴上的幅度归一化。CNN里一般只做去训练集的均值。
②卷积计算层
神经网络是全连接的,而卷积神经网络是局部关联的,
该层功能:
每个神经元看作一个滤波器filter,filter对局部数据计算。取一个数据窗口,这个数据窗口不断地滑动,直到覆盖所有样本
参数介绍:
a. 深度depth:神经元个数,决定输出的depth厚度?。
b. 步长stride:决定滑动多少步可以到边缘
c. 填充值zero-padding:在外围边缘补充的圈0个数,方便从初始位置以步长为单位可以刚好滑倒末尾位置,通俗地讲就是为了总长能被步长整除。
③激励层-ReLU
该层功能:激励层有激励函数,把卷积层输出结果做非线性映射。非线性的映射有:Sigmoid、Tanh、ReLU、Leaky ReLU、ELU、Maxout等,大多数用的是ReLU。
参数介绍:
a. Leaky ReLU:不会“饱和” /挂掉,计算也很快。
b. 指数线性单元ELU:所有ReLU有的优点都有,不会挂,输出均值趋于0,因为指数存在,计算量略大。
c. Maxout:计算是线性的,不会饱和不会挂,多了好些参数;
m a x ( ω T 1 x + b 1 , ω T 2 x + b 2 ) m a x ( ω 1 T x + b 1 , ω 2 T x + b 2 ) max(ωT_1x+b_1,ωT_2x+b_2)max(ω_1Tx+b_1,ω_2Tx+b_2) max(ωT1x+b1,ωT2x+b2)max(ω1Tx+b1,ω2Tx+b2)
④池化层
该层功能:
池化层夹在连续的卷积层中间,用于压缩数据和参数的量、减小过拟合。
参数介绍:池化层有 Max pooling 和 average pooling两种方式,工业界多用Max pooling。
⑤全连接层
该层功能:全连接层中,两层之间所有神经元都有权重连接,通常全连接层在卷积神经网络尾部,因为尾部的信息量没有开始那么大。