大数据入门——搜索广告的文本点击率预估（python实现）2019高校大数据挑战赛

这是我的第三篇博文。数据来源于某高校大数据比赛，可以去官网自行下载。由于比赛时间与期末考试冲突的原因，线下模型已经搭建，但是线上数据没有运行完毕，所以没进复赛，虽然线上数据运行完成也不一定会晋级啦，但还是蛮可惜的。代码对我已经没什么用处啦，就开源在博客里吧。转载须注明作者、出处。由于本人水平有限，有些代码会有冗余，欢迎大家批评、指正、讨论、交流。
如有需要请加我的QQ：623862392，当然，需要在验证信息中说明来意。
好，闲话少说，我们开始。

列名	类型	示例
query_id	int	3
query	hash string，term空格分割	1 9 117
query_title_id	title在query下的唯一标识	2
title	hash string，term空格分割	3 9 120
label	int，取值{0, 1}	0

这是比赛官网提供的说明，数据的格式如上表所示。
估计大家没怎么看清楚，其实只是这样的话我也看不懂。我截取了一部分数据，如下图所示：
从左到右，第一列、第二列…一直到第五列，依次是上表所对应的query_id、query、query_title_id、title、label

文本点击率预估

概念解释

相信大家都有过使用百度搜索某样东西，弹出广告的经历。你搜索的时候，会发出一个query，网络会返回给你一个title，这个title就是你搜索出来的广告标题，query就是你在百度中搜索的那段话。大家可以看到数据样式。第一列是query_id其实很容易理解，就是把你搜索的内容编上号嘛，第二列为什么是数字呢？因为根据官网给出的信息，这些词都是脱敏后的词汇哈希处理以后的形成的，是哈希字符。换句话说，就是把一篇文章中所有的词都编上号，用词的序号来代替原来字母或者汉字表示的词。这样做出于什么样的考虑呢？在这里我就不做过多介绍了，搜索相关关键词以后应该会有很多文章会详细阐述哈希处理的用法。第三列是title_id，第四列是title，是发送一个query以后返回的内容。注意，一个query可以对应多个title，这个很好理解，任何人在百度上搜某个东西，都会弹出好多个网页链接吧？对，这个就是这个意思。每一个title就是一个广告。那么我在看到这些个广告以后，有没有点击这个广告呢？这就是第五列——label，所表述的，0代表没有点击，1代表点击。
我们把思路梳理一下，上述过程其实正好是搜索广告的过程。想象一下，你打开了百度或者谷歌，输入了一段话，这段话是一个query，然后敲击回车键，百度瞬间返回了好几个广告标题，这些标题内容就是title，你犹豫了一下，选了一个点击进去了，于是乎这个title所对应的label值，为1，剩下的你没有点击的，label值是0。（当然也存在把返回的所有title都点击了一遍的可能性，不做过多赘述）
至于点击率的问题，可以理解为点击的概率，也就是label为1的概率。独立重复试验频率是逼近于概率的嘛，也就是说，我们预测每条数据label是1的概率，即为文本点击率预估。

思路分析

本题还是属于文本挖掘的范畴，只不过这次我们直接处理哈希字符，可以忽略词语本身的意思，不需要分词、数据清洗，也不需要导入词库、设置停用词，倒是省了不少的麻烦。
一般说来，文本点击率预估的特征提取，都是以各种相似度特征为基础的。而文本本身的特征，用处倒不是特别多。比如词频逆文档特征，在这里就不太好用了。原因很简单，数据太多，词语太多，导致词频矩阵维度特别高，稀疏度也特别高，处理起来相当麻烦。当然，这里说不能直接使用，不是说不能用，我们完全可以利用词频文档矩阵生成相似度特征，下文会提到。
那什么是文本相似度特征？简言之，就是两段话的相似度。在这里，就是query和title的相似度。试想一下，你为什么要在百度中搜索一段话呢？你肯定是想找到合意的东西。如果说返回的title和你的query即搜索内容，几乎一样，你是不是觉得你已经找到想要的东西了？那点击他的概率是不是就大一些了？就是这个道理。我们完全有理由猜测，文本相似度和点击率成正相关的关系，当然，一切交给数据，我们站在前人研究的基础上选择了文本相似度，具体什么关系我们不去管它。
我们再次回到宏观视角，现在问题已经转化成了：“如何提取相似度特征”和“选用何种算法模型进行预测”这两个问题了。相信大家应该都有些熟悉了吧？
下面，是详细步骤，及代码。

具体步骤

一、工具、原料（gensim包的配置、导入）

本项目需要用到库/包：numpy、pandas、sklearn、scipy、gensim
下面我简单讲一下gensim怎么装
n多人被gensim搞到头晕眼花直骂街。原因就在于，gensim需要依赖numpy和scipy，但是在装这两个包的时候，版本各式各样，不一定和gensim兼容。假如你可以成功导入gensim，当我没说，好吧？请直接跳过步骤一阅览步骤二；假如你确实发现，咦？我明明安装成功，但是怎么导不进来呢？那么本文很可能是你的救命稻草。
首先提供一个网站，下载对应版本包的网站https://www.lfd.uci.edu/~gohlke/pythonlibs/
其次，如何判断自己当前版本应该下载什么包呢？在这里提供给大家两个命令：
针对AMD64，有：

import pip._internal
print(pip._internal.pep425tags.get_supported())

针对WIN32，有：

import pip
print(pip.pep425tags.get_supported())

我话还没说完，这两个命令，请针对python的版本，在命令行窗口中运行。当然，要先用命令行窗口打开python，在Python环境下才行。
运行完成后，会得到类似这种：

根据cp35，cp35m，win_amd64之类的，在刚刚贴出来的那个网站中，寻找合适的包。（看哪个包名称有这些字符，你会懂得）
然后，将你下载的包放到合适的位置，再安装。这里的合适的位置，是确保你的开发环境搜索的到的位置，不然一会还是不能成功导入。一般，如果你安装了anaconda，跟其他anaconda环境下的包安装地址一样，一般是没有问题的。下载完成之后，在命令行窗口中，cd到那个包的位置，然后pip install，就OK了。
这时，在命令行中打开python运行，import gensim是一定可以的，但在集成开发环境中就不一定了，这说明已经兼容，但是开发环境还没搜索到。这就是刚刚说的那个问题：“确保开发环境能够搜索的到你的包。”
已经到这一步了，估计重新安装打死都不愿意，所以，完全可以在搜索路径中添加你安装的这个地址。需要用到sys包，使用方法如下：

import sys
#print(sys.path)
sys.path.append("c:\\users\\administrator\\appdata\\local\\programs\\python\\python37-32\\lib\\site-packages\\")

比如我是安在c:\users\administrator\appdata\local\programs\python\python37-32\lib\site-packages\目录下的，那我就把这个地址添加进去就好了。注意地址要用双斜线。
这可以说是有史以来最全的导入gensim包的步骤了。
如果这样还不成功。。。。。。天晓得你遇到了怎么样的摧残。

二、基于词频逆文档矩阵的相似度

导入必要的包，导入数据

Created on Fri May 31 21:25:46 2019

@author: MXB
"""

import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from scipy.spatial.distance import pdist
from sklearn import model_selection as ms
#导入数据
data=pd.read_csv("train_data.csv",header=-1)
y = data.iloc[:,4].values

相似度，是什么之间的相似度？答曰：向量间的相似度，我们将问题转化为：找到能代表文本特征的向量，比较向量之间的相似度。
现有两个向量分别代表两个文本，向量元素是文本词频，那么这两个向量在空间上越接近，夹角越小，或者距离越近，是不是就越相似？如图所示。不再赘述。

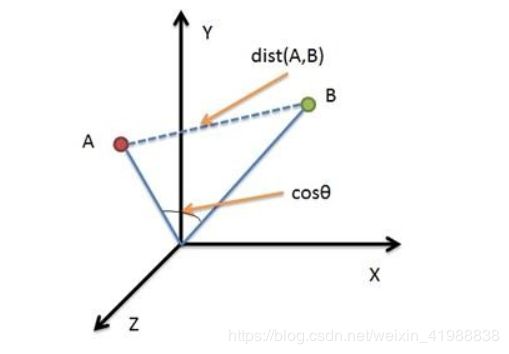
下面的操作很关键。我将数据的每一行的第二列和第四列，即query与title合并成一列（例如，就第一行数据来说，把第四列放在第一列的下面，新形成一个两行的小表格），再对这列文本进行词频逆文档处理，可以保证提取出的特征维度一致。我们用其词频逆文档矩阵当作其词频向量，计算向量间距离、相似度。由于对每一行都要进行列合并的操作，势必要用到循环语句。这样做的考虑主要还是为了解决每个文本词数不一致的问题，词数不一致即向量维度不一致，就无法进行向量间运算。词频逆文档统计形成的小表格中两行所有的词汇形成特征作为各自的向量，维度自然就一致了。
（如果对词频逆文档矩阵有疑问请参考我的上一篇博客）

#提前预备好数据框，作为存储特征的容器
cossim1= pd.DataFrame()
ChebyDistance1=pd.DataFrame()
ManhatDistance1=pd.DataFrame()
CorDistance1=pd.DataFrame()
eucldist_vectorized1=pd.DataFrame()
	
#利用词频逆文档矩阵提取特征
for i in range(len(data)):
    global datacos1
    global datacos2									#变量声明
    datacos1 = pd.Series(data.iloc[i,1])	#提取同一行的两列（query列和title列）
    datacos2 = pd.Series(data.iloc[i,3])
    d = pd.concat([datacos1,datacos2],ignore_index=True) #将两列合并为一列
    vec = TfidfVectorizer()
    Y = vec.fit_transform(d.values)
    m = Y.todense()									#m是query和title的词频逆文档矩阵
    Y1 = m[:1]											#Y1是query列的词频逆文档特征
    Y2 = m[1:]											#Y2是title列的词频逆文档特征
 	 #计算余弦相似度
    X1 = np.vstack([Y1,Y2])
    cossim11 = pd.DataFrame(1 - pdist(X1,'cosine'))
    cossim1=cossim1.append(cossim11)	#将每一行提取的余弦相似度累加在表格下一行存储起来
 	 #计算切比雪夫距离、曼哈顿距离、欧几里得距离、皮尔逊相关系数（按照出现次序排列）
    Y3=np.array(Y1)
    Y4=np.array(Y2)
    ChebyDistance11=pd.DataFrame(pd.Series(np.max(np.abs( Y3-Y4))))
    ChebyDistance1=ChebyDistance1.append(ChebyDistance11)
   
    ManhatDistance11=pd.DataFrame(pd.Series(np.sum(np.abs(Y3-Y4))))
    ManhatDistance1=ManhatDistance1.append( ManhatDistance11)
   
    eucldist_vectorized11= np.sqrt(np.sum((Y3 - Y4)**2))
    eucldist_vectorized11= pd.DataFrame(pd.Series(eucldist_vectorized11))
    eucldist_vectorized1=eucldist_vectorized1.append(eucldist_vectorized11) 
  
    CorDistance11=pd.DataFrame(pd.Series(1-np.corrcoef(Y3,Y4)[0,1]))
    CorDistance1=CorDistance1.append(CorDistance11)

#注意，这里已经出for循环了，我们将得到的特征进行填充缺失值处理。
#缺失值出现的原因请读者自己探索。
cossim1=cossim1.reset_index(drop=True)
cossim1=cossim1.fillna(0)
eucldist_vectorized1=eucldist_vectorized1.reset_index(drop=True)
ChebyDistance1= ChebyDistance1.reset_index(drop=True)
ManhatDistance1=ManhatDistance1.reset_index(drop=True)
CorDistance1=CorDistance1.reset_index(drop=True)
CorDistance1=CorDistance1.fillna(0)

其实有些特征加进去反而会降低模型分数，我只是先把代码贴出来。

三、基于集合运算的相似度（jaccard、tanimoto）

jaccard系数的计算原理，两个集合的公共部分占并集之比，即共现相似度。

tanimoto系数计算原理，亦成为广义jaccard。

代码实现如下：

from math import*
from decimal import Decimal
import pandas as pd
import numpy as np
data=pd.read_csv("train_data.csv",header=-1)

def jaccard(a,b):
    a=ws3
    b=ws4
    ret1 = [ i for i in a if i not in b ]
    ret11=str(ret1)
    ret12=ret11.split(" ")
    lenret12=len(ret12)
    union1=set(a).union(set(b))
    union11=str(union1)
    union12=union11.split(" ")
    lenunion12=len(union12)
    jaccardsim=lenret12/lenunion12
    return jaccardsim

def tanimoto(p,q):
    moto1 = [v for v in p if v in q]
    moto11=str(moto1)
    moto12=moto11.split(" ")
    lenmoto12=len(moto12)
    p11=str(p)
    p12=p11.split(" ")
    lenp12=len(p12)
    q11=str(q)
    q12=q11.split(" ")
    lenq12=len(q12)
    return lenmoto12 / (lenq12 + lenp12 - lenmoto12)

ws1=np.array(data[1])
ws2=np.array(data[3])
ws1=ws1.tolist()
ws2=ws2.tolist()
jaccardsim1=pd.DataFrame()
tanimotosim1=pd.DataFrame()
for i in range(len(data)):
    ws3=[ws1[i]]
    ws4=[ws2[i]]
    jaccardsim11=jaccard(ws3,ws4)
    jaccardsim11=pd.DataFrame(pd.Series(jaccardsim11))
    jaccardsim1=jaccardsim1.append(jaccardsim11)
    tanimotosim11=tanimoto(ws3,ws4)
    tanimotosim11=pd.DataFrame(pd.Series(tanimotosim11))
    tanimotosim1=tanimotosim1.append(tanimotosim11)
jaccardsim1=jaccardsim1.reset_index(drop=True)
tanimotosim1=tanimotosim1.reset_index(drop=True)

三、基于词向量的相似度

import gensim
import pandas as pd
import numpy as np
data=pd.read_csv("train_data.csv",header=-1)
dataword2vec2 = pd.concat((data[1],data[3]), axis=1)
dataword2vec3=np.array(dataword2vec2)
dataword2vec3=dataword2vec3.tolist()		  #必须用列表类型的数据才能训练词向量
model = word2vec.Word2Vec(dataword2vec3, size=300, hs=1, min_count=1, window=3)
ws1=np.array(dataword2vec2[1])
ws2=np.array(dataword2vec2[3])
ws1=ws1.tolist()
ws2=ws2.tolist()																	
word2vecsim1=pd.DataFrame()
for i in range(len(data)):
    ws3=[ws1[i]]
    ws4=[ws2[i]]
    word2vecsim2=model.wv.n_similarity(ws3,ws4)		#计算两列的相似度
    word2vecsim2=pd.DataFrame(pd.Series(word2vecsim2))
    word2vecsim1=word2vecsim1.append(word2vecsim2)
word2vecsim1=word2vecsim1.reset_index(drop=True)

四、合并训练

我们选用余弦相似度、词向量相似度、jaccard系数、tanimoto系数、欧氏距离、皮尔森相关系数作为特征，合并预测（使用这几个特征效果最好）

import pandas as pd
import scipy
#将特征单独形成一个数据框
te= pd.concat((cossim1,word2vecsim1,jaccardsim1,tanimotosim1,eucldist_vectorized1,cosresult1), axis=1)
te=pd.read_csv("chusaitezheng.csv")		#写出特征成csv格式文件保存备用

#	切分训练集与测试集
from sklearn import model_selection as ms
X_train,X_test,y_train,y_test = ms.train_test_split(te2,data[4],test_size=0.1,random_state=10)

我们选用逻辑回归预测，时间原因没有用双模型，但是效果也还不错。

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(C=1.0)  # 默认使用L2正则化避免过拟合，C=1.0表示正则力度(超参数，可以调参调优)
clf.fit(X_train, y_train)
test_pro = clf.predict_proba(X_test)
test_pro1=pd.DataFrame(test_pro)

模型评价，计算auc得分

from sklearn import metrics
test_auc = metrics.roc_auc_score(y_test,test_pro1.iloc[:,1] )#验证集上的auc值
print( test_auc )

总结

最后模型的线下得分如果我没有记错的话，应该是0.5714，进复赛需要前一百名，第一百名auc貌似是0.55？考虑到线上模型可能会有一些浮动，我只能说，如果当时数据做完的话，还是有可能进复赛的，毕竟我只用了单模随便跑了跑，精力主要在特征上。不过，结束了就是结束了，抛开功利性因素，我成长了很多很多。下一次比赛可能离我很遥远了，毕竟自己越来越忙。想想2019年这整个上半年，我都在电脑屏目前紧皱眉头眯缝着眼睛，也是感慨良多。写这篇文章，一是做个记录，毕竟好记性不如烂笔头。二是做个纪念，纪念我又一次地挑战自我。最后，在这里我要特别感谢王雄学长，为我在学习“机器学习”的过程中提供了莫大的帮助。
以上。