机器视觉第二次大作业

内容
给定图像，消除其中的周期性干扰

以下为处理过程：
1、显示图像的傅里叶变换后的频谱和傅里叶变换对数所得的频谱：

从图2 可以明显的看出周期性噪声在频谱上的分布，于是在低中高频段上都有分布，但是低
通部分较少，所以考虑使用低通滤波器；
此部分代码：

I=imread('C:\Users\18868\Desktop\陶瓷基片周期性噪声滤波.jpg');
%导入图像 I2=rgb2gray(I); s=fftshift(fft2(I2)); imshow(abs(s),[]);
%图像傅里叶所得的频谱 imshow(log(abs(s)),[]);
%图像傅里叶变换对数所得频谱

2、使用理想低通滤波器：


画面出现了意料之外的弯曲，即使周期性噪声已经不太明显。考虑使用别的低通滤波器，使得画面更加平滑。
此部分代码

    [a,b]=size(s);
    a0=round(a/2);
    b0=round(b/2);
    d=12;
    for i=1:a
    for j=i:b
    distance=sqrt((i-a0)^2+(j-b0)^2);
    if distance<=d
    h=1;
    else
    h=0;
    end
    s(i,j)=h.*s(i,j);
    end
    end
    s=uint8(real(ifft2(ifftshift(s))));
    imshow(s)
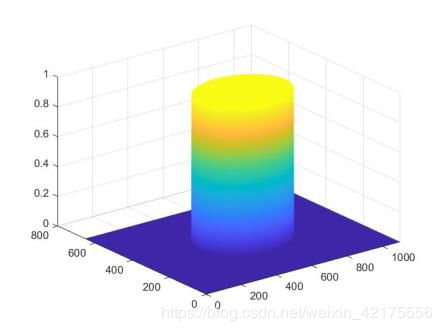
    Hd=ones(size(I2));
    Hd(r>0.2)=0;
    figure
    surf(Hd,'Facecolor','interp','Edgecolor','none','Facelighting','pho
    ng');%三维

3、Butterworth 低通滤波器的使用：
通过查阅资料了解到，巴特沃斯低通滤波器对图像有较好的平滑滤波效果，于是尝试在本次
作业中使用，效果如下所示：


虽然平滑效果很好，但是可以看到抹去了很多细节，如果需要对边缘细节进行判断我们还要进行别的处理。
此部分代码

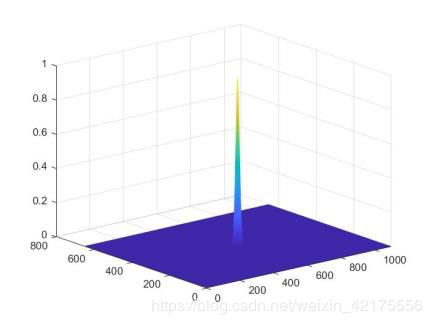
   [f1,f2]=freqspace(size(A2),'meshgrid');%Butterworth 低通滤波器
    D=50/size(A2,1);
    r=f1.^2+f2.^2;
    Hd=ones(size(A2));
    for i=1:size(A2,1)
    for j=1:size(A2,2)
    t=r(i,j)/(D*D);
    Hd(i,j)=exp(-t);
    end
    end
    Y=fft2(double(A2));
    Y=fftshift(Y);
    Ya=Y.*Hd;
    Ya=ifftshift(Ya);
    Ia=real(ifft2(Ya));
    figure;
    imshow(uint8(Ia));
    surf(Hd,'Facecolor','interp','Edgecolor','none','Facelighting','pho
    ng');%三维

4、锐化处理突出边缘
在使用巴特沃斯低通处理之后，虽然滤波效果和平滑效果很好，但是如果对边缘细节有要求，
还需要进行锐化处理，我们使用Roberts 算子进行锐化处理。效果如下：

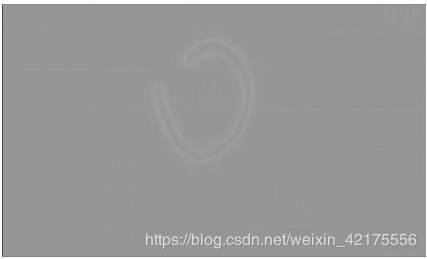
但是画面的亮度因此下降，可以考虑后续的上色处理。
此部分代码

%图像锐化
[m,n]=size(Ia);
Ia=double(Ia);
b=zeros(m,n);
c=zeros(m,n);
for i=1:m-2
for j=1:n-2
b(i+1,j+1)=Ia(i,j)-Ia(i+1,j+1);
c(i+1,j+1)=Ia(i,j+1)-Ia(i+1,j);
b(i+1,j+1)=sqrt(b(i+1,j+1)^2+c(i+1,j+1)^2)+150;
end
end
figure;
imshow(uint8(b));