【线代】学习笔记:3Blue1Brown-线性代数的本质-2
前言:辗转反侧焦虑失眠起床读书
关于行列式的计算公式(面积改变),可以通过下图理解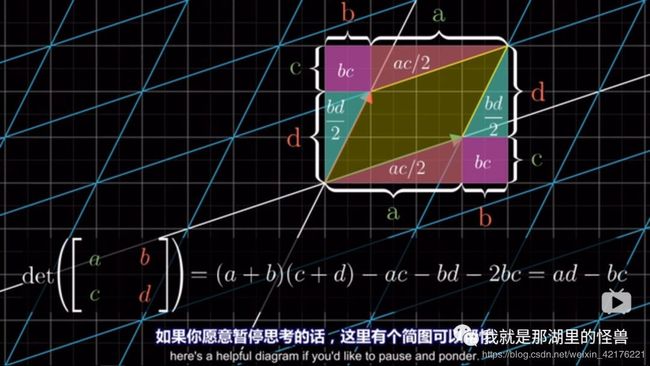
关于矩阵与线性方程组Ax=v
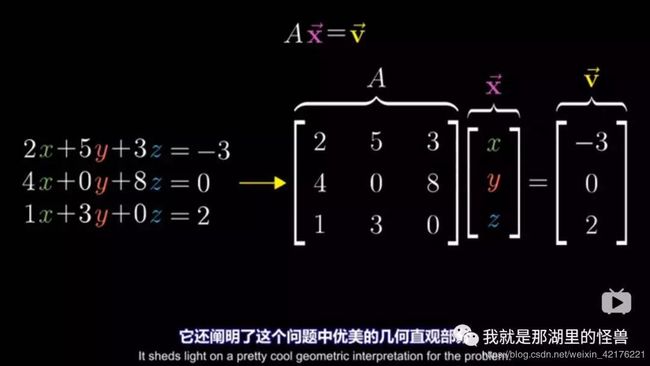
求解意味着我们去寻找一个向量x,使得他在变换后与v重合
首先看看最可能的情况,即A的行列式不为零
在这种情况下,有且仅有一个向量与v重合
并且你可以通过逆向进行变换来找到这个向量:
A逆乘A等于一个“什么都不做”的矩阵
这个什么都不做的变换被称做“恒等变换”
但当行列式为零时,
与这个方程组相关的变换将空间压缩到更低的维度上
此时没有逆变换
你不能将一条线“解压缩”为一个平面
至少这不是一个函数能做的
因为这样要求将一个单独的向量变换为一整条线的向量
但是函数只能将一个输入变换为一个输出
即便不存在逆变换,解仍然可能存在
比如说一个变换将空间压缩为一条直线
你得足够幸运,让向量V恰好处在这条直线上

有些零行列式的情况比其他的更加严格当变换的结果为直线时(一维)
称变换的秩为1
秩=变换后空间的维数
所有可能的输出向量Av(变换结果)构成的集合称为矩阵的“列空间”
换句话说,列空间就是矩阵的列所张成的空间(一定有零向量)
所以秩=变换后空间的维数=(精确)列空间的维数
对于一个满秩变换来说,
唯一能在变换后落在原点的就是零向量本身
对于一个非满秩矩阵,他将空间压缩到一个更低的维度上,
也就是会有一系列向量在变换后成为零向量
举个例子,如果一个二维线性变换将空间压缩到一条直线上
那么沿一个不同方向直线上的所有向量就被压缩到原点
如果一个三维线性变换将空间压缩到一个平面上
同样也会有一整条线上的向量在变换后落在原点
如果一个三位线性变换将空间压缩到一条直线上
那么就有一整个平面上的向量在变换后落在原点
在变换后落在原点的向量集合
被称为所选矩阵的“零空间”或“核”
变换后一些向量落在零向量上,从这个意义上说,
“零空间”就是这些向量所构成的空间
对线性方程组而言,但v恰好为零向量时,
零空间给出的就是这个向量方程的所有可能解
要求两个向量v和w的点积:
将投影的长度与向量v的长度相乘
你就得到了他们的点击v和w
这个解释十分不对称
这对两个向量的处理完全不同
点积和顺序呈现无关性,
下面从直观上来理解
如果v与w的长度恰好相同。我们可以利用其中的对称性
因为w向V上投影,并将w的投影长度与v的长度相乘
和V向w上投影,并将v的投影和w的长度相乘互为镜像
现在如果你将其中一个缩放若干倍,对称性被破坏了
但我们可以这样解读新向量的点积
如果你认为w向v上投影,这是因为
将v放大为原来的两倍并不改变w的投影长度
但是被投影的向量长度变为原来的两倍
另一方面,假设你想将v投影到w上
这次是投影的长度变为原来的两倍
但是被投影的向量长度保持不变
所以总体效果只是点积变为两倍
如何理解投影和对应坐标相乘并将结果相加的联系?
从“对偶性”开始讨论
(多维空间到一维空间(数轴)的线性变换)
高维空间中的变换需要满足一些严格的性质才会具有线性,
但是为了不偏离目标,忽略这些内容
而聚焦于一种与之等价的直观特性:
如果你有一系列等距分布于一条直线上的点,
然后应用变换
线性变换会保持这些点等距分布在输出空间(数轴)上
否则这个变换不是线性的
只不过,这些基向量这次只落在一个数上
所以当我们将他们变换后的位置记录为矩阵的列时
矩阵的每列只是一个单纯的数
假设你有一个线性变换,他的i帽和j帽分别变换至1和-2
将向量4(4,3)分解为4乘i帽加上3乘j帽
由于线性性质,在变换后
这个向量的位置是4乘变换后的i帽,也就是1
加上3乘以变换后的j帽,也就是-2
结果说明它落在-2上

感觉上就和两个向量的点积一样

举个例子,现在考虑一个二维向量
他的终点落在数轴的1上
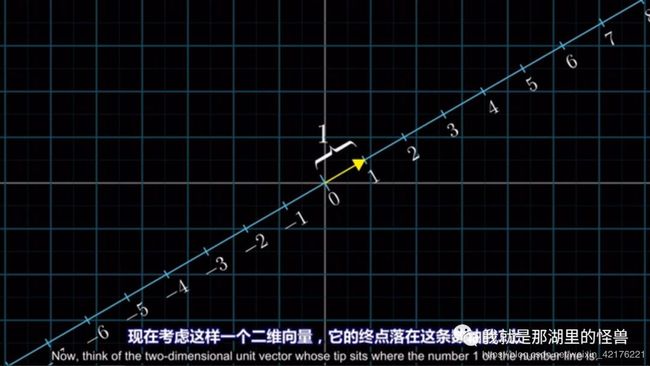
给他起名为u帽
如果我们将二维向量直接投影到这条数轴上
实际上,我们就这样定义了一个从二维向量到数的函数
更重要的是,这个函数是线性的,因为它顺利通过了线性检验
所以,根据投影矩阵[?,?]
我们定义了一个从二维向量到数的线性变换
考虑变换后i帽和j帽的位置(因为他们就是线性变换矩阵的列)
答案应该是U帽向x轴投影所得到的数:
u帽的x坐标给出了i帽向u帽所在数轴投影所得到的数
y坐标同理

所以,空间中任意向量经过投影变换的结果
和这个向量与u帽的点积在计算上完全相同

也就是投影矩阵与这个向量相乘
和这个向量与u帽(投影矩阵的对偶向量)的点积
在计算上完全相同

这就是为什么与单位向量的点积可以解读为
将向量投影到单位向量所在直线上所得到的投影值。
非单位向量点积时,
只需将其中一个视为单位向量
点积后进行缩放即可。
小结:
我们有一个从二维空间到数轴的线性变换
他并不是由向量数值或点积运算定义得到的
而只是通过将空间投影到给定数轴上来定义
但是因为这个变换是线性的
所以它必然可以用某个12矩阵描述
又因为12矩阵与二维向量相乘的计算过程
和转置矩阵并求点积的计算过程相同

所以这个投影变换必然会与某个二维向量相关
就这一意义而言,应用变换与向量v做点积是一样的
总而言之:
两个向量点乘,
就是将一种一个向量转化(横置)为线性变换,
不把他看做空间中的箭头
而把它看作线性变换的物质载体。
对于二维向量的叉积
你需要将v的坐标作为矩阵的第一列
w的坐标作为矩阵的第二列
然后直接计算行列式
因为上面的2 *2矩阵与一个将i帽和j帽分别移至v和w的线性变换相对应
行列式就是关于变换前后面积变化比例的度量(有向)
但严格意义上讲,这个度量(叉积)不是真正的叉积
真正的叉积是通过两个三位向量生成一个新的三位向量(注意是向量)
但我们还是要考虑这两个向量所围成的平行四边形,
而这个平行边形的面积依然会发挥巨大的作用:
首先叉积得到向量,行列式得到数。
叉积向量的结果是向量而不是数,
向量的方向与平行四边行垂直,遵循右手法则
每当你看到一个(多维)空间到数轴的线性变换时
它都与那个空间中的唯一一个向量所对应,也就是说
应用线性变换与这个向量点乘等价
数值上说,这事因为这类线性变换可以用一个只有一行的矩阵描述
而它的每一列给出了变换后基向量的位置
将这个矩阵与某个向量V相乘在计算上
与将矩阵倾倒得到的向量和V点乘相同。
这里的收获在于
每当你看到一个从空间到数轴的线性变换
你都能够找到一个向量(称为这个变换的对偶向量)
是的应用线性变换与对偶向量点乘等价
我要做的是定义一个从三维空间到数轴的特定线性变换
并且它是根据向量V和W来定义的
然后当我们将这个变换与三维空间中的对偶相关联时
这个对偶向量就会是V和W的叉积
之所以这么做,是因为理解这个变换能够
解释清楚叉积的计算过程和几何含义之间的关系
二维向量的叉积为+/-平行四边形的面积
如果你并不知道三维向量的叉积并尝试去往外推
你可能会想,它涉及三个向量,u,v,和w.
将他们的坐标作为一个3 *3矩阵的列
然后计算这个矩阵的行列式
从几何上讲,这个行列式给出了三个向量所章程的平行六面体的体积
外加一个正负号,取决于这三个向量是否满足右手定则
当然,你们都知道这不是三维向量的叉积
真正的三位向量的叉积接受两个向量并输出一个向量而不是接收三个向量并输出一个数
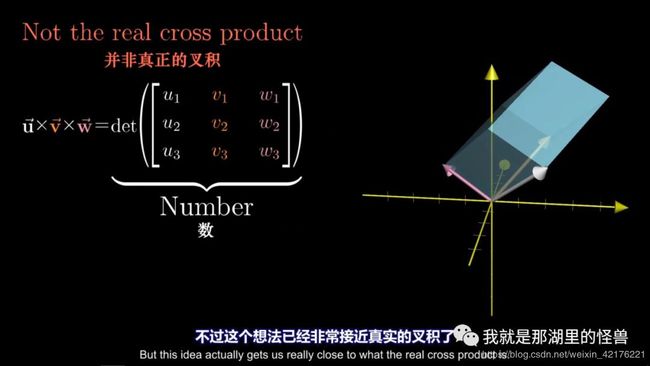
不过这个想法已经非常接近真实的叉积了
将第一个向量U看作可变向量,比如(x,y,z),而V和W保持不变
那么我们就有一个从三维空间到数轴的函数了(输入变量向量和两个已知向量,输出常数)
你输入一个向量(x,y,z),然后通过3 *3矩阵的行列式得到一个数
这个向量的第一列是(x,y,z),其余两列是常向量v和w的坐标
这个函数的几何意义是,对于任一输入的向量(x,y,z)
你都考虑它和v与w确定的平行六面体
得到他的体积,然后根据取向确定符号
这个函数的一个至关重要的心智在于它是线性的
一旦你知道它是线性的,我们就能开始引进对偶性的思想了
一旦知道他是线性的,你就可以通过矩阵乘法来描述这个函数
具体地说,因为这个函数从三维空间到一维空间
就会存在一个1*3矩阵来代表这个变换
而对偶性的整体思路是
从多维空间到一维空间的变换的特别之处,在于你可以将这个矩阵立起来,
并且将整个变换看作与这个特定向量的点积
我们要找的就是这个特殊的三位向量,称之为P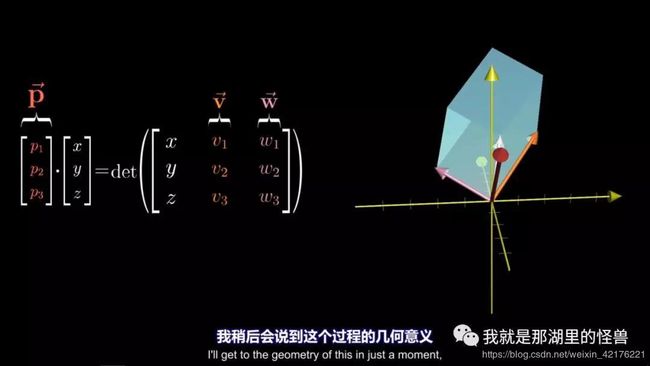
使得P与其他任一向量(X,Y,Z)的点积等于一个3 *3矩阵的行列式。
这个3 *3矩阵的第一列为(x,y,z),其余两列分别为V和W的坐标
稍后讨论这个过程的几何意义,但现在先专注于他的计算意义
使得P与其他任一向量(X,Y,Z)的点积等于一个3 *3矩阵的行列式。
这个3 *3矩阵的第一列为(x,y,z),其余两列分别为V和W的坐标
稍后讨论这个过程的几何意义,但现在先专注于他的计算意义
P与向量(x,y,z)点乘输出的结果是某个数乘以x,加上某个数乘以y,加上某个数乘以z
这里的某些书就是p的坐标
但是当你计算等号右边的行列式时,你可以将其整理为
某个常数乘以x,加上某个常数乘以y,加上某个常数乘以z
这里的某些常数涉及了v和w坐标的特定组合
因此这些v和w坐标的特定组合,就是我们寻找的向量p的坐标

以上奇怪的运算过程可以看作是一下问题的答案:
当你将向量p和某个向量(x,y,z)点乘时,所得结果等于一个3 * 3矩阵的行列式,
这个行列式第一列为(x,y,z),其余两列分别为V和W的坐标
什么样的向量P才能满足这一特殊性质?
现在再问一次相同的问题。不过这次,要从几何的角度回答,而不是从计算的角度
当你将向量p和某个向量(x,y,z)点乘时,所得结果等于一个由(x,y,z)和v与w确定的平行六面体的有向体积(行列式为体积数值)
什么样的向量P才能满足这一特殊性质?
记住一点,向量P与其他向量的点积的几何解释,是将其他向量投影到P上,然后投影长度与p的长度相乘
考虑到这一点,对于我们所关心的平行六面体的体积,以下说明一种思考方法
首先获得由v和w确定的平行四边形的面积,乘以向量(x,y,z)在垂直于平行系边形方向上的分量(不是(x,y,z)的长度)
换句话说,我们找到的线性函数对于给定向量的作用,是将这个向量投影到垂直于v和w的直线上,
然后将投影长度与v和w张成的平行四边形的面积相乘
但是,这和垂直于v和w且长度为平行四边形面积的向量与(x,y,z)点乘是同一回事
更重要的是,如果你选择了合适的向量方向,点积为负的情况就会与(x,y,z)、v和w满足右手定则的情况相吻合。
这意味着我们找到了一个向量P
使得P和某个向量(x,y,z)点乘时,所得结果等于一个3*3矩阵的行列式,
这个矩阵的三列分别为(x,y,z)、v的坐标和w的坐标
因此我们之前通过特殊符号技巧进行计算所得到的向量
必然在几何上与这个向量相对应
这就是叉积的计算过程与集合解释有关的根本原因
总结
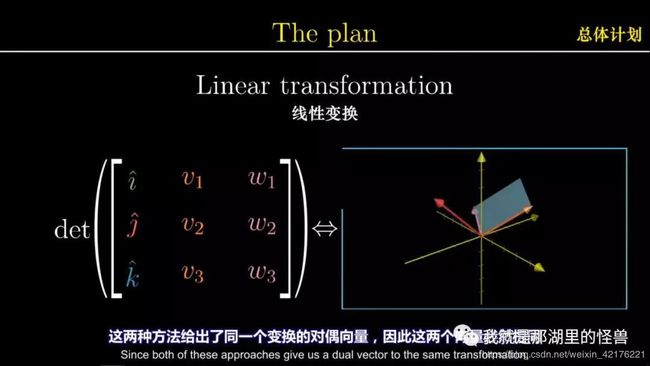
首先定义了一个三维空间到数轴的线性变换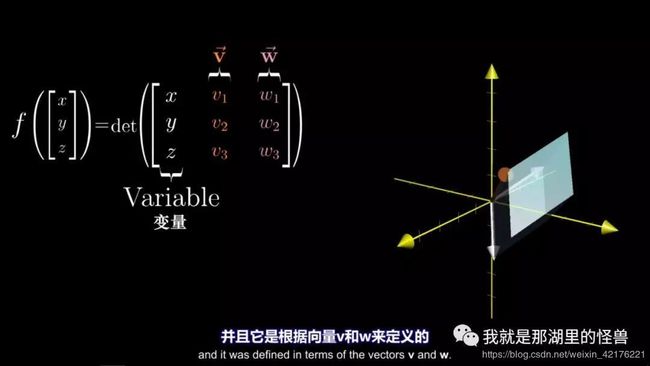
然后通过两种个不同给的方式来考虑这个变换的对偶向量
一方面,计算方法引导你使用下面这种技巧:在矩阵第一列列出i帽、j帽和k帽,然后计算行列式

但是从几何角度思考,我们可以推断出这个对偶向量必然与v和w垂直,并且其长度两个向量张成的平行四边形的面积相同
这两种方法给出了同一个变换的对偶向量,因此这两个向量必然相同。
PS:
啊,叉积的一些想法!构造一个函数f(x,y,z)=det(,),里面是一个三乘三的矩阵,由三个列向量拼成,分别是转置后的(x,y,z),V向量和W向量。现在看这个函数的含义。 一方面!右边可以看作三个向量组成六面体的体积。这个体积等于V与W的点积(所构成平行四边形面积)乘以变量向量投影到同时垂直于V,W的直线的分量长度。 那么,这等价于是变量向量点乘 垂直于V,W且长度为V,W构成平行四边形面积的 向量p0(当然,应根据右手定则选择正确方向)。
另一方面!由于左边是个线性函数,而从右式可知这个函数是从三维到一维,那么等同于二维向量的叉积,函数可以被表示成对变量向量(x,y,z)的一个投影变换,而我们可以用一个1* 3的矩阵来代表这个变换(称作P),这里延伸到对偶性,所以可以视为一个3* 1的对偶向量和变量向量的点积。我们称这个对偶向量为p。而p的具体数值可以通过代数运算对应(方法在正文中)
最后我们再回过头看,p0和p不就是一样的吗!也就是这个变换P,可以说与 和对偶向量p/p0点乘 等价。。。