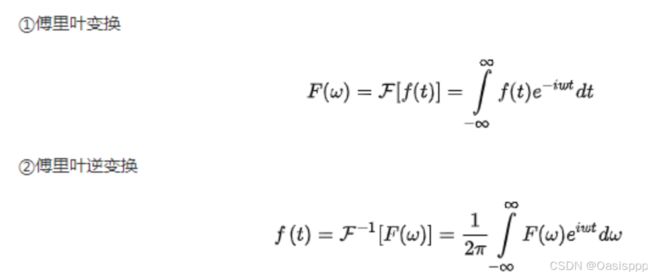计算机保研/考研面试题——数学篇

       笔者在2023年参加了部分985和华五计算机夏令营和预推免面试，遇到了不少数学问题，以下是笔者的一些总结，从高数、线代、概率论三个方面讨论。（对保研er和考研er均适用，如需要其他学科的问题请关注我~）

---

相关文章：

计算机保研/考研面试题——数据结构与算法篇-CSDN博客

计算机保研/考研面试题——操作系统篇-CSDN博客

计算机保研/考研面试题——计算机网络篇-CSDN博客

计算机保研/考研面试题——编程语言篇（C和C++）-CSDN博客

计算机保研/考研面试题——数据库基础篇-CSDN博客

计算机保研/考研面试题——计算机组成原理篇-CSDN博客

---

一、高等数学

1. 解释什么是极限。

       在函数中，当自变量趋近于某个特定值时，函数的取值可能会逼近某个确定的数值，这个确定的数值就被称为函数的极限。

定义：

       给定一个函数f(x)，当自变量x趋近于某个特定值x0时，如果函数的取值f(x)随着x的趋近逼近一个确定的数A，那么我们称A是函数f(x)在x趋近于x0时的极限。

       对于任意给定的正数ε，存在另一个正数δ，使得当 0 < |x - x0| <δ时，对应的函数值满足|f(x) - A| <ε。（任意ε，存在δ， 0 < |x - x0| <δ，|f(x) - A| <ε）

2. 解释一下罗尔中值定理。

       如果一个函数在闭区间上连续，在开区间内可导，并且在区间的两个端点处取相同的值，那么在这个区间内，必然存在至少一个导数为零的点。

3. 解释一下拉格朗日中值定理。★★

       如果一个函数在闭区间上连续，在开区间内可导，则至少存在一个点，该点的导数等于函数在区间端点的斜率。

4. 解释一下柯西中值定理。

       对于函数f(x)和g(x)，如果它们在闭区间[a, b]上连续，并且在开区间(a, b)内可导，那么存在一个点c∈(a, b)使得：

       [f(b) - f(a)]/[g(b) - g(a)] = f'(c)/g'(c)

       存在一个点c，使得函数f(x)和 g(x)在区间[a, b]上的平均变化率等于它们在点c处的瞬时变化率的比值。

5. 三个中值定理的区别、联系和应用。★★★

       罗尔中值定理适用于闭区间内连续的函数。当函数在闭区间的端点上取相同的值时，罗尔中值定理保证函数在开区间内至少有一个导数为零的点。

       拉格朗日中值定理适用于闭区间内连续且可导的函数。它是罗尔中值定理的推广，保证函数在开区间内至少有一个导数等于平均变化率的点。拉格朗日中值定理应用：在某个时间点，质点的瞬时速度等于它在某个时间段内的平均速度。

       柯西中值定理适用于两个函数在闭区间内连续且可导。它是拉格朗日中值定理的推广，表示两个函数在开区间内的平均变化率等于它们在开区间内某个点的瞬时变化率的比值。

6. 解释一下泰勒公式。★★★

       泰勒公式的初衷是用多项式函数来近似表示函数在某点周围的情况。

       泰勒公式可用于将一个函数在某个点附近展开成无穷级数的形式。

       泰勒公式的一般形式如下：

       f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)²/2! + f'''(a)(x - a)³/3! + ...

       f(x) 是要近似的函数，a 是展开点。

7. 泰勒展开中皮亚诺余项和拉格朗日余项的区别。★★★

       皮亚诺余项通常使用函数在展开点的高阶导数来表示，通过将剩余的高阶导数项乘以展开点到近似点的距离的幂次来估计误差大小。

       拉格朗日余项使用函数在展开区间内某一点处的高阶导数来表示，并且乘以展开区间长度的适当幂次。拉格朗日余项在整个展开区间上都有较好的估计效果。

       总体而言，皮亚诺余项主要用于提供粗略的近似值与截断后误差的估计，而拉格朗日余项则提供更精确的近似值与实际值之间的误差估计。

8. 一阶导和二阶导的物理意义和几何意义是什么？

       一阶导数表示函数的变化率或切线的斜率，二阶导数表示一阶导数的变化率。

       在物理上，一阶导数可以表示速度，二阶导数可以表示加速度。

       在几何上，一阶导数可以表示切线斜率，二阶导数可以表示曲线的凸性和凹性。

9. 一元函数和多元函数可导、可微、连续和可积的关系。★★

       一元函数：可导和可微等价。可导一定连续，连续不一定可导（y=|x|，在x=0处不可导）。

       多元函数：可微一定可导，可微一定连续，偏导连续一定可微，偏导存在不一定连续。

10. 什么是方向导数和梯度★★

       方向导数是一个标量。方向导数可以理解为函数在某个点的某个方向上的变化速率。

       梯度是一个向量。它包含了函数在每个方向上变化最快的信息。对于一个多变量函数 f(x, y, z)，其梯度定义为：

       ∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)

       梯度的方向是函数在某一点上变化最快的方向，而梯度的模长表示了函数在该点上的变化速率（或最大方向导数）。

       梯度的几何意义：

       函数变化增加最快的地方。沿着梯度向量的方向，更容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，更容易找到函数的最小值。

       梯度的应用：

       势场：在物理场的描述中，梯度常常用来表示场的强度和方向。例如，在电场中，梯度表示电势场的变化率。

       最速下降法：梯度在优化问题中发挥重要作用。它利用梯度的负方向来搜索函数的最小值。根据最速下降法，沿着梯度的负方向进行迭代更新可以逐步接近函数的最小值。

       方向导数和梯度的关系：

       如果我们知道了函数在某一点的梯度向量，以及一个表示方向的单位向量，就可以计算出函数在这个方向上的方向导数。

       方向导数=某点的梯度与给定方向的方向余弦做内积（点乘）。

11. 什么是傅里叶级数和傅里叶变换。★★

       傅里叶级数：任何周期性函数若满足狄利克雷条件，那么该函数可以用正弦函数和余弦函数构成的无穷级数来表示。

       傅里叶变换：可以处理非周期性信号（一个信号可以看成一个周期性无穷大T->∞的信号）。傅里叶变换将一个信号从时域转换到频域，得到该信号的频谱。

       应用：

       通过傅里叶变换，我们可以对信号进行滤波、降噪、压缩、频谱估计等操作。这些技术在音频处理、图像处理、视频压缩、通信系统等领域都有广泛应用。

二、线性代数

12. 什么是矩阵的秩？★★★

       基本概念

       k 阶子式：在一个矩阵或行列式中取k行k列，交叉处的k²个元素按原顺序构成的行列式。

       [1] 从子式的角度定义：矩阵的秩就是矩阵中非零子式的最高阶数。

       [2] 从极大线性无关组的角度定义：矩阵的所有行向量中极大线性无关组的元素个数。

       [3] 从标准型的角度定义：求一个矩阵的秩，可以先将其化为行阶梯型，非零行的个数即为矩阵的秩。

13. 什么是线性相关和线性无关？★★★

       线性相关：

       如果存在不全为零的系数，使得向量集合果中的某些向量的线性组合等于零向量，那么这些向量就被称为线性相关的。换句话说，如有向量v₁、v₂、v₃、...、vₙ，并且存在不全为零的标量c₁、c₂、c₃、...、cₙ，使得c₁v₁+ c₂v₂+ c₃v₃+ ... + cₙvₙ= 0，则这些向量就是线性相关的。

       线性无关：

       如果向量集合中的向量无法通过任何非平凡的线性组合（即非所有系数都为零）得到零向量，那么这些向量就是线性无关的。换句话说，如果 c₁v₁ + c₂v₂ + c₃v₃ + ... + cₙvₙ = 0 的唯一解是 c₁=c₂=...=cₙ=0，则这些向量就是线性无关的。

14. 一个矩阵线性无关的等价定义有什么？

       非奇异矩阵（行列式不为0）、矩阵可逆、矩阵满秩、特征值没有 0。

15. 向量组的极大无关组和向量组的秩是什么。

       极大无关组是指在向量组中选择尽可能多的线性无关向量，使得这个子集仍然保持线性无关，并且再添加任何其他向量，就会使得它变得线性相关。

       向量组的秩等于它的极大无关组合中向量的个数。

16. 向量空间（线性空间），向量空间的基与维数是什么。

       n 维向量构成的非空集合V，对于向量加法和数乘两种运算封闭。则这个V是向量空间。

       基：

       设 V是一向量空间，a1,a2,...,ar∈V 且满足:

       a) a1,a2,...,ar线性无关;

       b) V中向量均可由 a1,a2,..., ar 线性表示

       则称 a1,a2,...,ar 为V 的一个基。

       维数

       基中所含向量个数 r 称为向量空间的维数

17. 什么是矩阵的特征值与特征向量？特征值有什么应用？★★★★

       定义：

       给定一个n×n的方阵A，若非零向量x满足Ax = λx，那么λ称为A的特征值。非零向量x称为A的特征向量。

       也就是说，特征向量x在经过矩阵 A 的线性变换后，只会改变长度但不会改变方向，而特征值则表示该变换的缩放比例。

       计算：

       |λE-A|=0从而求得所有λ。将λi带回(λiE-A)x=0那么可求得方程组的基础解系，特征值为λi的特征向量就是基础解系的线性组合。

       性质：

       所有特征值的积是该矩阵的行列式（行列式的本质是特征值的乘积），所有特征值的和是该矩阵的迹。

       应用：

       特征空间变换：特征向量可以用于将矩阵对角化，从而简化线性变换的描述。这在计算中能够提高效率。

       图像处理：特征值和特征向量可以用于图像压缩、降噪和特征提取等领域。例如，主成分分析（PCA）方法就利用了特征向量来提取图像中的关键特征。

       数据分析：特征值可以用于降维和数据拟合。例如，在主成分分析中，我们可以通过保留最大的特征值对应的特征向量进行数据降维，从而捕捉数据的主要变化趋势。

18. 特征值为0和矩阵的秩的关系。★★

       如果 λ = 0，则有以下结论：

       A的秩小于n

如果 A 的某个特征值为 0，那么 A 的秩必定小于 n。这是因为特征值为 0 表明 A 不是满秩矩阵，存在线性相关的列向量，导致 A 的秩小于 n。

       A的行向量和列向量中至少有一个线性相关

       如果 λ = 0，那么对应的特征向量 x 满足 Ax = 0。由于 x ≠ 0，说明存在一个非零的向量使得 A 与它的乘积为零。这意味着 A 的行向量和列向量中至少有一个线性相关。

       特征值为 0 并不意味着矩阵 A 的秩一定为 0。

19. 什么是相似矩阵和相似对角化？★★

       相似矩阵定义：

       两个n×n的矩阵A和B称为相似矩阵，如果存在一个可逆矩阵P，使得B = P^(-1) AP。

       相似矩阵性质：

       相似矩阵具有相同的特征值、秩、行列式。

       相似矩阵的特征向量可以通过相似变换得到。

       相似对角化定义：

       相似对角化是指将一个矩阵A通过相似变换P^(-1) AP转化为对角矩阵D的过程。D 的对角线上的元素就是 A 的特征值，P 的列向量就是 A 的特征向量。

       并不是所有的矩阵都可以相似对角化。一个矩阵可对角化的充要条件是它具有n个线性无关的特征向量。

20. 什么是对称矩阵？对称矩阵有什么性质？★★★

       定义：

       方阵A中，aij = aji，则A为对称矩阵，或A^T = A。若A还是实矩阵，则A为实对称矩阵。

       性质：

       特征值都是实数，特征向量都是实向量。

       不同特征值对应的特征向量正交。

       对称矩阵可以通过正交相似变换对角化，即存在正交矩阵P，使得 (P^T)AP = D，D 是对角矩阵。

（补充：正交矩阵就是满足PP^T=E）

21. 什么是二次型？什么是正定矩阵？正定矩阵的性质是什么？★

       二次型：

       二次型是一个关于变量的二次多项式表达式。对于 n 维向量 x = [x₁, x₂, ..., xₙ]，二次型可以表示为 Q(x) = (x^T )A x，其中 A 是一个对称矩阵。

       正定矩阵：

       给定一个n阶实对称矩阵，若对于任意长度n的非零向量x，有(x^T)Ax>0恒成立，则A是一个正定矩阵。

       正定矩阵的性质：

1. 正定矩阵是实对称矩阵，即 A = A^T。这意味着矩阵的元素关于主对角线对称。
2. 所有特征值都大于0，行列式|A| > 0，r（A）= n，为满秩矩阵；正定矩阵是可逆的，其逆矩阵也是正定的。
3. 如果两个矩阵A和B都是正定矩阵，A+B和AB也是正定的。
4. 正定矩阵的n次方仍然是正定矩阵。

       半正定矩阵：

       给定一个n阶实对称矩阵，若对于任意长度n的非零向量x，有(x^T)Ax≥0恒成立，则A是一个半正定矩阵。所有特征值都大于等于0。

22. 什么是矩阵合同？★

       若A和B是两个方阵，若存在可逆矩阵Q，使得B=(Q^T)AQ成立，则A与B合同。

       合同的充要条件：对A和行和列施以相同的初等变换变成B。

三、概率论与数理统计

23. 什么是条件概率？

       在事件 B 发生的条件下，事件 A 发生的概率记为 P(A|B)，读作 “A 在 B 条件下发生的概率”。

条件概率的计算公式如下： P(A|B) = P(AB) / P(B)

       P(AB)表示事件A和事件B同时发生的概率。

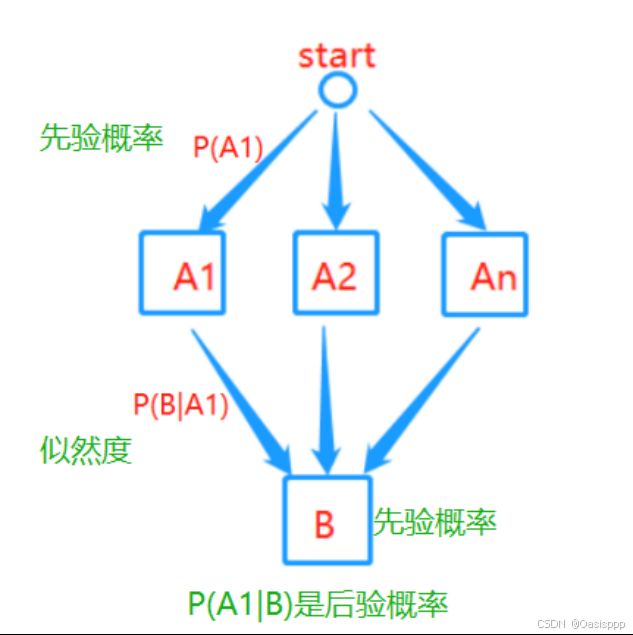
24. 什么是全概率公式和贝叶斯公式？★★★★★★

                           

       全概率公式：

       如果有一些互斥事件A1,A2,……,An，它们的并集是全集，则任何事件B发生的概率可以拆分为每一个Ai∩B的概率和。

       P(B)=P(A1)*P(B|A1)+P(A2)*P(B|A2)+...+P(An)*P(B|An)

       机器学习中的贝叶斯公式：

       P(A|B) = (P(B|A) * P(A)) / P(B)

       P(A|B) 是后验概率，P(B|A) 是似然度，P(A) 表示事件 A 的先验概率，P(B) 表示事件 B 的先验概率。

       贝叶斯公式的实际意义：

       贝叶斯公式将我们对于事件A发生的先验概率与新获得的证据（似然度）相结合，从而得到在给定证据的情况下事件 A 发生的后验概率。

       例如：

       P(咳嗽患支气管炎)=P(支气管炎有咳嗽症状)*P(支气管炎)/P(咳嗽)

       P(支气管炎有咳嗽症状)是似然度，容易求得。P(支气管炎)和P(咳嗽)是先验概率。这样帮助医生根据症状预测患者患某种病的概率。

       贝叶斯公式应用：

       机器学习中贝叶斯分类器：根据已有的训练样本和特征信息，利用贝叶斯公式计算不同类别的后验概率，从而进行分类任务。

       医学诊断与预测：通过将病人的先验概率与各种医学测试的似然度相结合，可以计算出某种疾病的后验概率，辅助医生进行诊断和预测。

25. 什么是先验概率和后验概率？★★★★★

       先验概率：

       事情未发生，只根据以往数据统计，分析事情发生的可能性，即先验概率。

       后验概率（贝叶斯公式）：

       事情已发生，已有结果，求引起这事发生的因素的可能性，由果求因，即后验概率。

       后验概率和先验概率的关系：

       后验概率的计算，是以先验概率为前提条件的。如果只知道事情结果，而不知道先验概率，是无法计算后验概率的。

26. 正态分布有什么性质？

1. 对称性：正态分布是概率密度函数关于其均值μ的对称分布，即在平均值两侧呈镜像对称。
2. 唯一峰值：正态分布的概率密度函数呈现单峰形状，只有一个最高峰值。
3. 分布范围无界：正态分布的取值范围是负无穷到正无穷，没有明确的上下界限。
4. 标准差决定形状：正态分布的形状由其标准差σ决定。较小的标准差会使曲线更加陡峭，较大的标准差会使曲线更加平坦。
5. 68-95-99.7 规则：在正态分布中，约有68%的观测值落在均值的一个标准差范围内，约有95%的观测值落在两个标准差范围内，约有99.7%的观测值落在三个标准差范围内。
6. 中心极限定理：多个随机变量的总和（或平均值）趋向于正态分布，即使原始随机变量不满足正态分布，这是中心极限定理的重要推论。

27. 什么是二元正态分布？有什么性质？

       二元正态分布是由两个连续随机变量组成的概率分布。它通常用来描述两个变量之间的关系和相互依赖性。每个变量都服从正态分布，而二元正态分布则描述了这两个变量之间的联合分布。

       性质：

1. 边缘分布：在二元正态分布中，每个随机变量的边缘分布都是正态分布。也就是说，如果我们只考虑其中一个变量，将另一个变量积分或求和消除，所得到的分布将是单个变量的正态分布。
2. 条件分布：二元正态分布中的每个随机变量的条件分布也是正态分布。条件分布是指在已知另一个变量的取值后，考虑该变量的分布。换句话说，给定一个变量的取值后，另一个变量的条件分布仍然是正态分布。
3. 相关性：二元正态分布中的两个变量之间存在线性相关性。相关系数 ρ 衡量了这种相关性的强度，它的取值范围为 -1 到 1。当相关系数为 0 时，表示两个变量相互独立；当相关系数为正值时，表示两个变量呈正相关关系；当相关系数为负值时，表示两个变量呈负相关关系。
4. 协方差：二元正态分布中的两个变量之间存在协方差。协方差描述了两个变量的线性关系程度，它的值可以为正、负或零。当协方差为正值时，表示两个变量呈正相关关系；当协方差为负值时，表示两个变量呈负相关关系；当协方差为零时，表示两个变量无线性相关性。

28. 什么是协方差和相关系数？★★

       协方差：

       协方差是用来衡量两个随机变量之间的总体线性关系强度和方向的指标。对于随机变量X和Y，其协方差记为Cov(X,Y)。协方差的计算公式如下：Cov(X,Y)=E((X-EX)(Y-EY))。

       相关系数（皮尔逊相关系数）：

       相关系数是通过归一化协方差得到的，用来度量两个变量之间线性相关程度的指标。

       ρ(X, Y) = Cov(X, Y) / (σx * σy)，σx 和 σy 分别表示 X 和 Y 的标准差。

       相关系数的取值范围在 -1 到 1 之间，-1 代表完全的负相关，1 代表完全的正相关，0 代表无线性相关。相关系数绝对值越接近1，相关程度就越强。

       其他：

       独立一定不相关，不相关不一定独立。

29. 什么是概率密度函数？★★

       概率密度函数是用来描述连续型随机变量的概率分布的函数。对于一个连续型随机变量 X，其概率密度函数 f(x) 定义了在给定区间内，随机变量 X 取某个特定取值的概率密度。

       概率密度函数 f(x) 是一个非负函数，并且满足以下两个性质：

       1）非负性：对于任意实数x，概率密度函数满足f(x)≥0。

       2）归一性：概率密度函数的总体积分等于1，即∫f(x)dx=1。

       EX=∫ xf(x)dx，DX=∫ x²f(x)dx

30. 什么是切比雪夫不等式？★★

       

       切比雪夫不等式给出了随机变量与其期望值之间的偏离程度的一个上界。

31. 什么是大数定律和中心极限定理？★★★★★★

       大数定律：

       对于独立同分布的随机变量序列 {X1, X2, X3, ..., Xn}，随着样本容量 n 的增大，样本均值的极限将趋于随机变量的期望值。换句话说，样本均值在大样本情况下趋于稳定并接近总体均值。

       三种大数定律（了解即可）：

       切比雪夫大数定律：样本数量n充分大时，n个是独立随机变量的平均数的离散程度很小。

       伯努利大数定律：将试验进行多次，随机事件的频率接近概率。

       辛钦大数定律：只要验证数学期望是否存在，就可判断其是否服从大数定律。

       中心极限定理：

       如果随机变量 X1, X2, ..., Xn 是独立同分布的，当样本容量 n 足够大时，样本的均值将近似地服从正态分布，即使原始总体并不服从正态分布。

       例如：10000人参加保险，一年内参加投保的人死亡的概率是0.006。设一年内参加投保的死亡人数X，X~B(10000，0.006)

       Ex=60，Dx=7.72²

       根据中心极限定理，近似X~N(60，7.72²)。

32. 什么是最大似然估计（极大似然估计）？★★★★

       最大似然估计就是一种参数估计方法。

       原理：

       利用已知的样本结果，反推最大概率导致这样结果的参数值。（根据结果推出参数）

       方程的解θ只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

       求最大似然估计量θ的一般步骤：

       [1] 写出似然函数；

       [2] 对似然函数取对数便于计算，并整理；

       [3] 求导数；

       [4] 解似然方程求出参数。

       应用：

       最大似然估计被用于参数估计、模型选择、假设检验等许多问题。