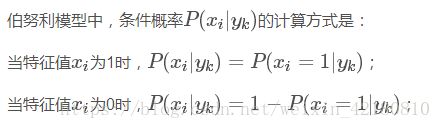机器学习之贝叶斯(贝叶斯定理、贝叶斯网络、朴素贝叶斯)
一、概率知识点复习
(1)条件概率
就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
(2)联合概率
可以简单的理解为事件A与事件B都发生的概率,记为P(AB)或P(A, B)。
此处就有 P(A, B) = P(A|B) * P(B)
若事件A与事件B独立,则有 P(A, B) = P(A) * P(B),这也说明了此时 P(A|B) = P(A)。
(3)全概率
如果事件B1,B2,B3,…,Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有:
P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn)
(这里我就只介绍这么多,大家如果对全概率不太理解的可以去补充补充!这点很重要,对后面理解贝叶斯很重要!!今天我重点在讲贝叶斯,所以此处就不在多讲全概率啦~~~后面的例子会涉及到!)
二、贝叶斯定理
我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)求得P(B|A)的道路。
此处我就给出贝叶斯定理的公式(其推导没必要知道)
(便于大家记忆,可以这样记P(A, B) = P(A|B) * P(B) 且P(A, B) = P(B|A) * P(A),大家将两式子合并会有P(A|B) * P(B) = P(B|A) * P(A))
便于大家记住这个公式在此有必要举个例子:
现有校准过的枪5把,没校准过的3把。现在某人用校准过的枪打靶中靶概率为0.8,用没校准过的枪中靶概率只为0.3。现在已知拿起一把枪打靶中靶了,请问这个枪是校准过的抢的概率?
(分析:直接套用上面的公式,但做P(A)的时候是要用到全概率的!!(全概率的重要性体现出来了~))
令中靶的事件为A,选中校准过的枪的事件为B1,选中未校准过的抢的事件为B2
则: P(B1) = 5 / 8 P(B2) = 3 / 8
P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) = 49 / 80
P(A|B1) = 4 / 5
上面的都做出来后,你会发现根据贝叶斯定理的公式是不是就可以求出P(B1|A)啦~
得: P(B1|A) = P(B1)P(A|B1) / P(A) = 40 / 49
思考:通过这个例子我们可以看到贝叶斯定理的作用,他就是打通了P(A|B1)求得P(B1|A)的道路,也可清晰理解到贝叶斯定理用来可分类!!
三、简聊贝叶斯网络
此章节只是为了让大家能看懂简单的贝叶斯网络图就ok~
贝叶斯网络,由一个有向无环图(DAG)和条件概率表(CPT)组成。 贝叶斯网络通过一个有向无环图来表示一组随机变量跟它们的条件依赖关系。它通过条件概率分布来参数化。每一个结点都通过P(node|Pa(node))来参数化,Pa(node)表示网络中的父节点。
如下图是一个简单的贝叶斯网络
![]()
其对应的全概率公式为:
P(a,b,c)=P(c∣a,b)P(b∣a)P(a)P(a,b,c)=P(c∣a,b)P(b∣a)P(a)
较复杂的贝叶斯网络
![]()
其对应的全概率公式为:
P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)
注意关系:一事件只与其父事件相关!!
四、朴素贝叶斯分类
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的正式定义如下:
1、设![]() 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合![]() 。
。
3、计算![]() 。
。
4、如果![]() ,则
,则![]() 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即:
![]() 。
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
![]()
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
![]()
根据上述分析,朴素贝叶斯分类的流程可以由下图表示(暂时不考虑验证):
![]()
五、朴素贝叶斯分类实例
下面讨论一个使用朴素贝叶斯分类解决实际问题的例子,为了简单起见,对例子中的数据做了适当的简化。
这个问题是这样的,对于SNS社区来说,不真实账号(使用虚假身份或用户的小号)是一个普遍存在的问题,作为SNS社区的运营商,希望可以检测出这些不真实账号,从而在一些运营分析报告中避免这些账号的干扰,亦可以加强对SNS社区的了解与监管。
如果通过纯人工检测,需要耗费大量的人力,效率也十分低下,如能引入自动检测机制,必将大大提升工作效率。这个问题说白了,就是要将社区中所有账号在真实账号和不真实账号两个类别上进行分类,下面我们一步一步实现这个过程。
首先设C=0表示真实账号,C=1表示不真实账号。
1、确定特征属性及划分
这一步要找出可以帮助我们区分真实账号与不真实账号的特征属性,在实际应用中,特征属性的数量是很多的,划分也会比较细致,但这里为了简单起见,我们用少量的特征属性以及较粗的划分,并对数据做了修改。
我们选择三个特征属性:a1:日志数量/注册天数,a2:好友数量/注册天数,a3:是否使用真实头像。在SNS社区中这三项都是可以直接从数据库里得到或计算出来的。
下面给出划分:a1:{a<=0.05, 0.05
2、获取训练样本
这里使用运维人员曾经人工检测过的1万个账号作为训练样本。
3、计算训练样本中每个类别的频率
用训练样本中真实账号和不真实账号数量分别除以一万,得到:
![]()
![]()
4、计算每个类别条件下各个特征属性划分的频率
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5、使用分类器进行鉴别
下面我们使用上面训练得到的分类器鉴别一个账号,这个账号使用非真实头像,日志数量与注册天数的比率为0.1,好友数与注册天数的比率为0.2。
![]()
![]()
可以看到,虽然这个用户没有使用真实头像,但是通过分类器的鉴别,更倾向于将此账号归入真实账号类别。这个例子也展示了当特征属性充分多时,朴素贝叶斯分类对个别属性的抗干扰性。
六、三种常见的朴素贝叶斯模型
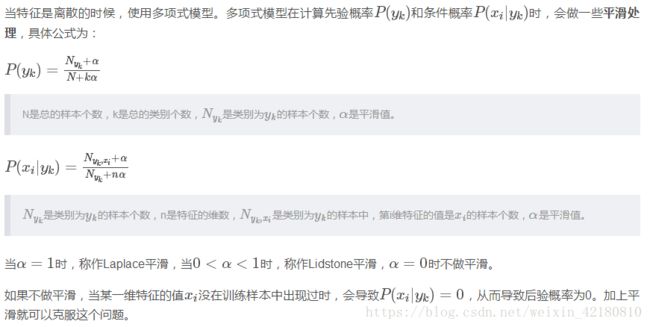
1. 多项式模型
2. 高斯模型
当特征是连续变量的时候,运用多项式模型就会导致很多P(xi|yk)=0P(xi|yk)=0(不做平滑的情况下),此时即使做平滑,所得到的条件概率也难以描述真实情况。所以处理连续的特征变量,应该采用高斯模型。
高斯模型假设每一维特征都服从高斯分布(正态分布):
3. 伯努利模型
与多项式模型一样,伯努利模型适用于离散特征的情况,所不同的是,伯努利模型中每个特征的取值只能是1和0(以文本分类为例,某个单词在文档中出现过,则其特征值为1,否则为0)。
七、朴素贝叶斯的优缺点
朴素贝叶斯的主要优点有:
1)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
4)不存在过拟合的说法。
朴素贝叶斯的主要缺点有:
1) 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
4)对输入数据的表达形式很敏感。
主要参考博客:
(1)张洋: http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
(2) https://blog.csdn.net/u012162613/article/details/48323777