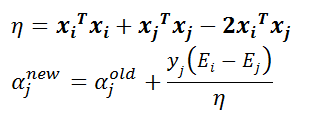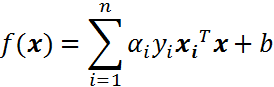《机器学习实战》—SVM
机器学习实战—SVM(支持向量机)
SVM
SVM - Support Vector Machine:支持向量机,其含义是通过支持向量运算的分类器。其中“机”的意思是机器,可以理解为分类器。在求解的过程中,会发现只根据部分数据就可以确定分类器,这些数据称为支持向量。
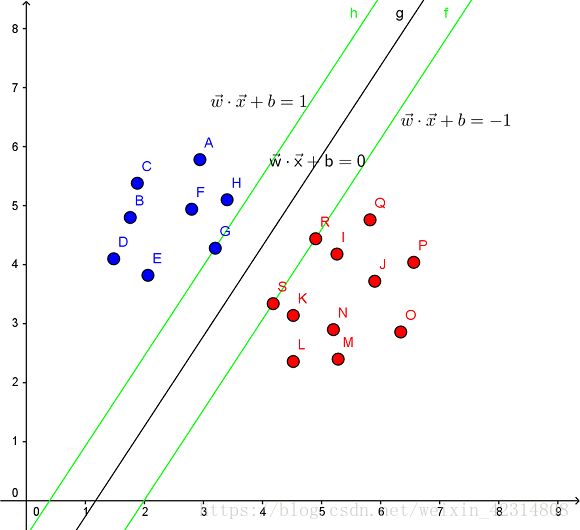
见下图,在一个二维环境中,其中点R,S,G点和其它靠近中间黑线的点可以看作为支持向量,它们可以决定分类器,也就是黑线的具体参数。
线性分类
在训练数据中,每个数据都有n个的属性和一个二类类别标志,我们可以认为这些数据在一个n维空间里。我们的目标是找到一个n-1维的超平面(hyperplane),这个超平面可以将数据分成两部分,每部分数据都属于同一个类别。
其实这样的超平面有很多,我们要找到一个最佳的。因此,增加一个约束条件:这个超平面到每边最近数据点的距离是最大的。也成为最大间隔超平面(maximum-margin hyperplane)。这个分类器也成为最大间隔分类器(maximum-marginclassifier)。
支持向量机是一个二类分类器。
f(x) = xw^T + b
w 和 b 是训练数据后产生的值。
KTT条件
核心思想
SVM的目的是要找到一个线性分类的最佳超平面f(x)=xwT+b=0。求 w 和 b。
首先通过两个分类的最近点,找到f(x)的约束条件。
有了约束条件,就可以通过拉格朗日乘子法和KKT条件来求解,这时,问题变成了求拉格朗日乘子ai 和 b。
对于异常点的情况,加入松弛变量ξ来处理。
使用SMO来求拉格朗日乘子ai和b。这时,我们会发现有些ai=0,这些点就可以不用在分类器中考虑了。
惊喜! 不用求w了,可以使用拉格朗日乘子ai和b作为分类器的参数。
非线性分类的问题:映射到高维度、使用核函数。
SMO算法优化
核心公式:
优化方法:
最外层循环,首先在样本中选择违反KKT条件的一个乘子作为最外层循环,然后用”启发式选择”选择另外一个乘子并进行这两个乘子的优化
在非边界乘子中寻找使得|E_i - E_j|最大的样本
如果没有找到,则从整个样本中随机选择一个样本
完整版SMO算法
完整版Platt SMO算法是通过一个外循环来选择违反KKT条件的一个乘子,并且其选择过程会在这两种方式之间进行交替:
在所有数据集上进行单遍扫描
在非边界α中实现单遍扫描
非边界α指的就是那些不等于边界0或C的α值,并且跳过那些已知的不会改变的α值。所以我们要先建立这些α的列表,用于才能出α的更新状态。
在选择第一个α值后,算法会通过“启发选择方式”选择第二个α值。
简化版SVM——SMO代码:
import matplotlib.pyplot as plt
import numpy as np
import random
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def selectJrand(i, m):
j = i
while (j == i):
j = int(random.uniform(0, m))
return j
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def showDataSet(dataMat, labelMat):
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1])
plt.show()
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
b = 0; m,n = np.shape(dataMatrix)
alphas = np.mat(np.zeros((m,1)))
iter_num = 0
while (iter_num < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print("L==H"); continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print("eta>=0"); continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小"); continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
alphaPairsChanged += 1
print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num,i,alphaPairsChanged))
if (alphaPairsChanged == 0): iter_num += 1
else: iter_num = 0
print("迭代次数: %d" % iter_num)
return b,alphas
def showClassifer(dataMat, w, b):
#绘制样本点
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
def get_w(dataMat, labelMat, alphas):
alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
return w.tolist()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet('testSet.txt')
b,alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
w = get_w(dataMat, labelMat, alphas)
showClassifer(dataMat, w, b)完整版SVM——SMO代码:
import matplotlib.pyplot as plt
import numpy as np
import random
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = np.shape(dataMatIn)[0]
self.alphas = np.mat(np.zeros((self.m,1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m,2)))
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def calcEk(oS, k):
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T) + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJrand(i, m):
j = i
while (j == i):
j = int(random.uniform(0, m))
return j
def selectJ(i, oS, Ei):
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei]
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i: continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
eta = 2.0 * oS.X[i,:] * oS.X[j,:].T - oS.X[i,:] * oS.X[i,:].T - oS.X[j,:] * oS.X[j,:].T
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("alpha_j变化太小")
return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
updateEk(oS, i)
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else:
return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter):
oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
else:
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
print("迭代次数: %d" % iter)
return oS.b,oS.alphas
def showClassifer(dataMat, classLabels, w, b):
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if classLabels[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
for i, alpha in enumerate(alphas):
if alpha > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
def calcWs(alphas,dataArr,classLabels):
X = np.mat(dataArr); labelMat = np.mat(classLabels).transpose()
m,n = np.shape(X)
w = np.zeros((n,1))
for i in range(m):
w += np.multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
if __name__ == '__main__':
dataArr, classLabels = loadDataSet('testSet.txt')
b, alphas = smoP(dataArr, classLabels, 0.6, 0.001, 40)
w = calcWs(alphas,dataArr, classLabels)
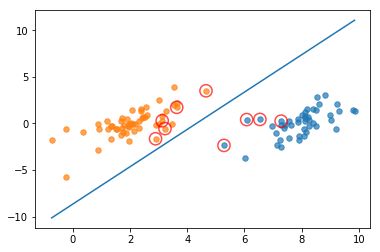
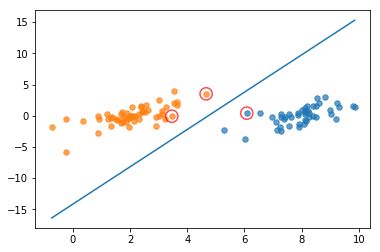
showClassifer(dataArr, classLabels, w, b)完整版SMO算法与简化版算法对比:
图中画红圈的样本点为支持向量上的点,是满足算法的一种解。完整版SMO算法覆盖整个数据集进行计算,而简化版SMO算法是随机选择的。可以看出,完整版SMO算法选出的支持向量样点更多,更接近理想的分隔超平面。
非线性SVM
核函数:
对于线性可分的平面其超平面方程:
参考文献
【1】Peter Harrington, Machine Learning inAction[M] . US 2007
【2】深入理解拉格朗日乘子和KTT条件