Matlab遗传算法用于旅行商问题优化TSP
Matlab遗传算法用于旅行商问题优化
- 要求
- 第一步:参数编码和初始群体设定
- 第二步:计算路径长度的函数设计
- 第三步:计算选择算子
- 第四步:计算交叉算子
- 第五步:计算变异算子
- 结果及分析
- MATLAB总代码
要求
利用遗传算法求旅行商问题的优化路径。设D={dij}是由城市i和j之间的距离组成的距离矩阵,旅行商问题就是求出一条通过所有城市且每个城市只通过一次的具有最短距离的回路。采用所遍历城市的顺序来表示各个个体的编码串,其等位基因为N个整数值或N个记号。以城市的遍历次序作为遗传算法的编码,目标函数取路径长度。在群体初始化、交叉操作和变异操作中考虑TSP问题的合法性约束条件(即对所有的城市做到不重不漏)。
设计利用遗传算法进行优化求解的程序,针对8个、15个、20个、30个城市情况下,分别给出最优路径下的城市顺序结果。
第一步:参数编码和初始群体设定
一般来说遗传算法对解空间的编码大多采用二进制编码形式,但对于TSP一类排序问题,采用对访问城市序列进行排列组合的方法编码,即某个巡回路径的染色体个体是该巡回路径的城市序列。
针对TSP问题,编码规则通常是N取进制编码,即每个基因仅从1到N的整数里面取一个值,每个个体的长度为N,N为城市总数。定义一个s行t列的pop矩阵来表示群体,t为城市个数N+1,即N+1,s为样本中个体数目。针对30个城市的TSP问题,t取值31, 即矩阵每一行的前30个元素表示经过的城市编号,最后一个元素表示经过这些城市要走的距离。
参数编码和初始群体设定程序为:
pop=zeros(s,N+1);%初始种群+适应度
for i=1:s %初始化
pop(i,1:N)=randperm(N);
end
第二步:计算路径长度的函数设计
在TSP的求解中,用距离的总和作为适应度函数,来衡量求解结果是否最优。将POP矩阵中每一行表示经过的距离的最后一个元素作为路径长度。
两个城市m和n间的距离为:
d m n = ( x m − x n ) 2 + ( y m − y n ) 2 . d_{mn} = \sqrt{(x_m-x_n)^2+(y_m-y_n)^2}\,. dmn=(xm−xn)2+(ym−yn)2.
通过样本的路径长度可以得到目标函数和自适应度函数。根据t的定义,两两城市组合数共有t-2组,则目标函数为:
J ( t ) = ∑ j = 1 t − 2 d ( j ) J(t) = \sum_{j=1}^{t-2} d(j) J(t)=j=1∑t−2d(j)
自适应度函数取目标函数的倒数,即:
f ( t ) = 1 J ( t ) f(t) = \frac{1}{J(t)} f(t)=J(t)1
第三步:计算选择算子
选择就是从群体中选择优胜个体、淘汰劣质个体的操作,它是建立在群体中个体适应度评估基础上。仿真中采用最优保存方法,即将群体中适应度最大的c个个体直接替换适应度最小的c个个体。
function [pop_ok]=ChooseParents(pop,N,s,c)%选择父代
pop=sortrows(pop,N+1);
for i=1:c
pop(i,:)=pop(s+1-i,:);
end
randIndex=randperm(size(pop,1));
pop=pop(randIndex,:);
pop_ok=pop;
end
第四步:计算交叉算子
交叉算子在遗传算法中起着核心的作用,它是指将个体进行两两配对,并以交叉概率将配对的父代个体加以替换重组而生成新个体的操作。
• 有序交叉法实现的步骤是:
步骤 1 随机选取两个交叉点crosspoint(1)和crosspoint(2); 步骤 2 两后代先分别按对应位置复制双亲X1和X2匹配段中的两个子串A1和B1; 步骤 3 在对应位置交换双亲匹配段以外的城市,如果交换后,后代X1中的某一城市a与子串中A1的城市重复,则将该城市取代子串B1与A1中的城市a具有相同位置的新城市,直到与子串A1中的城市均不重复为止,对后代X2也采用同样方法。
function [a,b]=CrossVariation(pop1,pop2,crosspoint,N)%交叉
A=pop1;
if(crosspoint(:,1)第五步:计算变异算子
变异操作是以变异概率对群体中个体串某些基因位上的基因值作变动。
这里采用倒置变异法:假设当前个体X为(1 3 7 4 8 0 5 9 6 2 ),如果当前随机概率值<变异概率,则随机选择来自同一个体的两个点mutatepoint(1)和mutatepoint(2),然后倒置该两个点的中间部分,产生新的个体。例如,假设随机选择个体X的两个点“7”和“9”,则倒置该两个点的中间部分,即将“4805”变为“5084”,产生新的个体X为(1 3 7 5 0 8 4 9 6 2)。
function [a]=Mutation(pop0,N)%变异
crosspoint=rand(1,2);
crosspoint=floor(crosspoint*N)+1;
if(crosspoint(:,1)结果及分析
当城市个数为8个时,初始化样本个数为100个,交叉概率为0.9,变异概率为0.2,最大迭代次数为200次,初始样本随机生成。
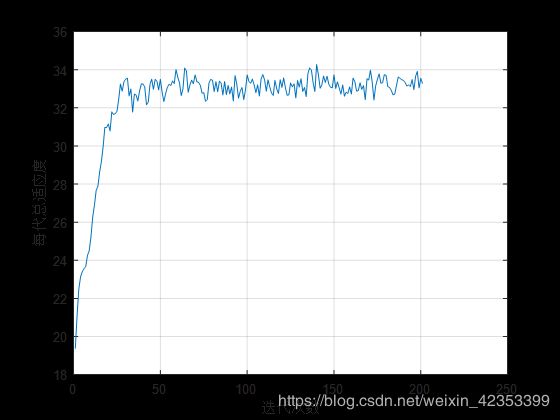
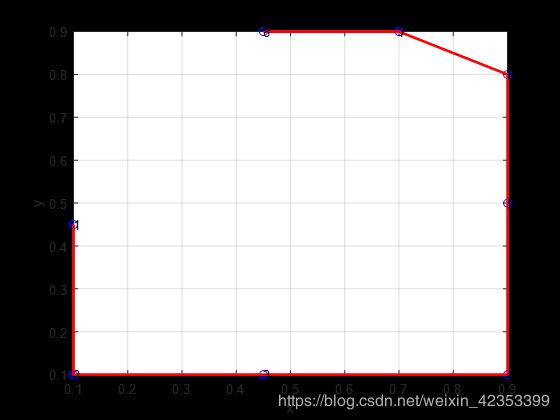
MATLAB总代码
function genetic_TSP1
clc;close all;clear all;
N=30;%城市数
city_coordinate=tsp(N);%城市位置
s=100;%样本数
c=30;%替换个数
pc=0.9;%交叉概率
pm=0.2;%变异概率
times=5000; %最大迭代次数
time=0; %实际迭代次数
pop=zeros(s,N+1);%初始种群+适应度
pop_fit_aver=[];%总适应度
min_dis=[];%最短距离
pop_min=[];%最短距离的基因
for i=1:s %初始化
pop(i,1:N)=randperm(N);
end
clf
plot(city_coordinate(:,1),city_coordinate(:,2),'ro');%画平均适应度折线图
for i=1:N
test_t=num2str(i);
text(city_coordinate(i,1),city_coordinate(i,2),test_t);%标号
end
grid on;
title('城市位置分布图');
xlabel('x');
ylabel('y');
city_distance=CityDistance(city_coordinate,N);%城市间距离
[individual_fit,sum,min1,min_index]=GroupFit(city_distance,N,pop,s);%适应度
sumP=sum;
pop_fit_aver=[pop_fit_aver;sum];
min_dis=[min_dis;min1];
pop(:,N+1)=individual_fit;
pop_min=[pop_min;pop(min_index,:)];
pop=ChooseParents(pop,N,s,c);%选择父代
for i=1:times
time=time+1;
E_new_new=[]; %子代
for j=1:s/2
a=rand(1);
b=rand(1);
if a>pc %交叉
;
else
crosspoint=rand(1,2);
crosspoint=floor(crosspoint*N)+1;
[pop(j,:),pop(j+s/2,:)]=CrossVariation(pop(j,:),pop(j+s/2,:),crosspoint,N);
end
if b>pm
;
else
pop(j,:)=Mutation(pop(j,:),N);
pop(j+s/2,:)=Mutation(pop(j+s/2,:),N);
end
E_new_new=[E_new_new;pop(j,:);pop(j+s/2,:)];
end
[individual_fit,sum,min1,min_index]=GroupFit(city_distance,N,E_new_new,s);
sumS=sum;
pop_fit_aver=[pop_fit_aver;sum];
min_dis=[min_dis;min1];
E_new_new(:,N+1)=individual_fit;
pop_min=[pop_min;E_new_new(min_index,:)];
if(abs(sumS-sumP)<0.001)%退出条件
break;
end
pop=ChooseParents(E_new_new,N,s,c);
end
[a,min_index]=min(min_dis);
a
time1=1:time+1;
figure%画平均适应度折线图
plot(time1,min_dis,'k.');
grid on;
title('每代最小值散点图');
xlabel('迭代次数');
ylabel('最短距离');
figure%画平均适应度折线图
plot(time1,pop_fit_aver);
grid on;
title('总适应度折线图');
xlabel('迭代次数');
ylabel('每代总适应度');
figure%画最优路径
DrawPath(city_coordinate,pop_min,min_index,N)
grid on;
title('最优路径图');
xlabel('x');
ylabel('y');
end
function [city_distance] = CityDistance(city_coordinate,N)%城市距离矩阵
city_distance=zeros(N,N);
for i=1:N
for j=1:N
city_distance(i,j)=((city_coordinate(i,1)-city_coordinate(j,1))^2+...
(city_coordinate(i,2)-city_coordinate(j,2))^2)^0.5;
end
end
end
function [individual_fit,num,min_distance,a] = GroupFit(city_distance,N,pop,s)%种群适应度
individual_distance=zeros(s,1);
for j=1:s
sum_distance=0;
for i=1:N-1
sum_distance=sum_distance+city_distance(pop(j,i),pop(j,i+1));
end
sum_distance=sum_distance+city_distance(pop(j,N),pop(j,1));
individual_distance(j,1)=sum_distance;
end
[min_distance,a]=min(individual_distance);
individual_fit=1./individual_distance;
num=0;
for i=1:s
num=num+individual_fit(i,1);
end
end
function [pop_ok]=ChooseParents(pop,N,s,c)%选择父代
pop=sortrows(pop,N+1);
for i=1:c
pop(i,:)=pop(s+1-i,:);
end
randIndex=randperm(size(pop,1));
pop=pop(randIndex,:);
pop_ok=pop;
end
function [a,b]=SwapRepeat(tbl,pop1,pop2,c1,c2,N)%基因去重
i=100/N;
for k=1:(c1-1)
if tbl(pop1(k),3)>i
kk=find(pop1(c1:c2)==pop1(k))+c1-1;
kkk=pop1(k);
pop1(k)=pop2(kk);
pop2(kk)=kkk;
end
end
for k=c2+1:N
if tbl(pop1(k),3)>i
kk=find(pop1(c1:c2)==pop1(k))+c1-1;
kkk=pop1(k);
pop1(k)=pop2(kk);
pop2(kk)=kkk;
end
end
a=pop1;
b=pop2;
end
function [a,b]=CrossVariation(pop1,pop2,crosspoint,N)%交叉
A=pop1;
if(crosspoint(:,1)<crosspoint(:,2))
pop1(crosspoint(:,1):crosspoint(:,2))=pop2(crosspoint(:,1):crosspoint(:,2));
pop2(crosspoint(:,1):crosspoint(:,2))=A(1,crosspoint(:,1):crosspoint(:,2));
while 1
tbl = tabulate(pop1(1:N));
if (tbl(:,3)<=(100/N))
break;
end
[pop1,pop2]=SwapRepeat(tbl,pop1,pop2,crosspoint(:,1),crosspoint(:,2),N);
end
else
pop1(crosspoint(:,2):crosspoint(:,1))=pop2(crosspoint(:,2):crosspoint(:,1));
pop2(crosspoint(:,2):crosspoint(:,1))=A(1,crosspoint(:,2):crosspoint(:,1));
while 1
tbl = tabulate(pop1(1:N));
if (tbl(:,3)<=(100/N))
break;
end
[pop1,pop2]=SwapRepeat(tbl,pop1,pop2,crosspoint(:,2),crosspoint(:,1),N);
end
end
a=pop1;b=pop2;
end
function [a]=SwapGene(sub,c1,c2)%交换
kk=ceil((c2-c1)/2);
kkk=(c2-c1)+2;
for k=1:kk
kkkk=sub(k);
sub(k)=sub(kkk-k);
sub(kkk-k)=kkkk;
end
a=sub;
end
function [a]=Mutation(pop0,N)%变异
crosspoint=rand(1,2);
crosspoint=floor(crosspoint*N)+1;
if(crosspoint(:,1)<crosspoint(:,2))
sub=pop0(crosspoint(:,1):crosspoint(:,2));
sub=SwapGene(sub,crosspoint(:,1),crosspoint(:,2));
pop0(crosspoint(:,1):crosspoint(:,2))=sub;
else
sub=pop0(crosspoint(:,2):crosspoint(:,1));
sub=SwapGene(sub,crosspoint(:,2),crosspoint(:,1));
pop0(crosspoint(:,2):crosspoint(:,1))=sub;
end
a=pop0;
end
function DrawPath(city_coordinate,E_new_new,min_index,N)%画路径图
k=E_new_new(min_index,1:N)
%plot(kkk(:,1),kkk(:,2),'b');%画平均适应度折线图
plot(city_coordinate(:,1),city_coordinate(:,2),'bo');
hold on;
for i=1:N-1
plot([city_coordinate(k(i),1),city_coordinate(k(i+1),1)],[city_coordinate(k(i),2),city_coordinate(k(i+1),2)],'r','LineWidth',2);
test_t=num2str(i);
text(city_coordinate(k(i),1),city_coordinate(k(i),2),test_t);
hold on;
end
test_t=[num2str(N)];
text(city_coordinate(k(N),1),city_coordinate(k(N),2),test_t);
end
function [cityn]=tsp(n) %城市位置
if n==8
city8=[0.1 0.1;
0.9 0.5;
0.9 0.1;
0.45 0.9;
0.9 0.8;
0.7 0.9;
0.1 0.45;
0.45 0.1];
cityn=city8;
elseif n==15
city15=[0.1 0.1;0.9 0.5;0.9 0.1;
0.45 0.9;
0.9 0.8;
0.7 0.9;
0.1 0.45;
0.45 0.1;
0.3 0.75;
0.2 0.1;
0.31 0.22;
0.35 0.25;
0.10 0.75;
0.80 0.35;
0.12 0.45];
cityn=city15;
elseif n==20
city20=[0.1 0.1;0.9 0.5;0.9 0.1;0.45 0.9;
0.9 0.8;0.7 0.9;0.1 0.45;0.45 0.1;0.3 0.75;
0.2 0.1;0.31 0.22;0.35 0.25;0.10 0.75;
0.80 0.35;0.12 0.45;0.67 0.17;0.85 0.32;
0.6 0.9;0.70 0.15;0.66 0.22];
cityn=city20;
elseif n==30
city30=[18 54;87 76;74 78;71 71;25 38;58 35;4 50;
13 40;18 40;24 42;71 44;64 60;68 58;83 69;58 69;54 62;51 67;37 84;
41 94;2 99;7 64;22 60;25 62;62 32;87 7;91 38;83 46;41 26;45 21;44 35];
cityn=city30;
end
end