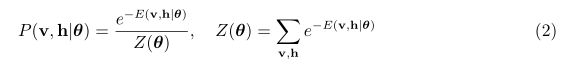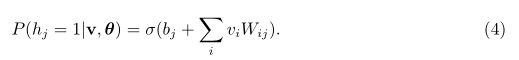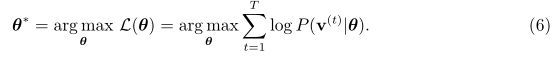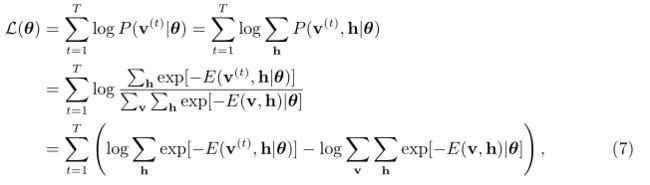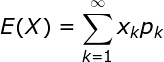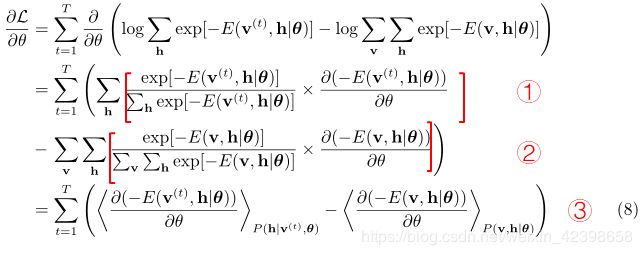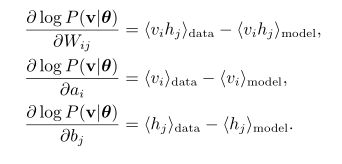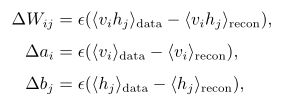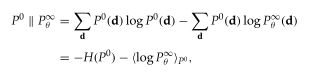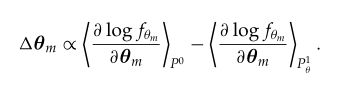深度学习 --- 受限玻尔兹曼机详解(RBM)

本节终于来到了重头戏受限玻尔兹曼机，为了能深入理解本节，我们深入讲了很多基础知识，这些基础知识很重要，是理解本节的基础，同时也是你学习其他算法的基础如强化学习、自然语言处理等。本节的安排是先对比一下受限玻尔兹曼机和玻尔兹曼机的区别，然后使用形式化语言讲一下学习过程和使用过程，最后 我们在逐一展开详细讲解，本节需要大家有点数学和概率论的基础当然矩阵知识也是需要一点的，这里的快速学习算法是CD（对比散度）算法，我们下面都会讲解到，废话不多说，下面开始：

受限玻尔兹曼机的结构特点

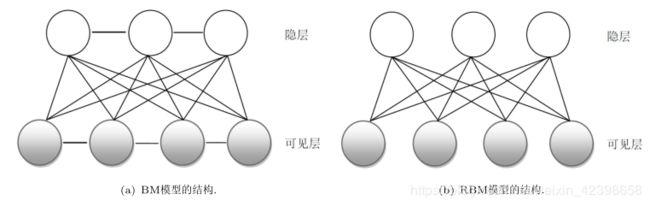
受限波尔兹曼机(Restricted Boltzmann Machines，RBM)是一类具有两层结构、对称连接且无自反馈的随机神经网络模型，层间全连接，层内无连接。我们知道玻尔兹曼机的是全连接的，这里我们对比一下看看：

这里先简单的说一下区别，然后再次介绍一下二者的工作原理，然后详细深入介绍背景，二者最大的区别在输入层和隐层的连接方式上，BM模型是全连接的而RBM是相互独立的，他们的区别就在这里，那么为什么计算量会差别那么大呢？在概率中我们知道BM模型的输入和隐层的概率计算肯定是联合概率，因为他们各自有联系而RBM的概率虽然函数联合概率，但是因为独立，可以单独计算每个神经元的概率，然后相乘，进而达到计算量小的目的，另外就是RBM的学习算法是对比散度即CDCD算法，学习速度很快，我们后面讲，那么二者的深入异同点是什么呢？这里还是先了解他们的学习机制在谈会更好，这里引用hinton论文里的文章的图进行讲解《Training Products of Experts by MinimizingContrastive Divergence》：                         

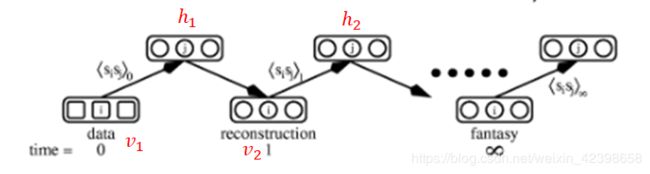
上图需要说明的是，上面的网络其实就是RBM的模型结构，只是说他这个训练过程为了让大家更清晰，所有展开了，那么我们来看看，他这里到底是怎么训练的，这里以手写体数字1和2来说明，首先我希望RBM能够记住我这个手写体的数字1和2，那么当我拿个新的1和2时，他可以准确的识别出来，因此这里在可见层输入数据data（例如手写体数字1和2）如上图的，刚开始网络的权值和偏置值会初始化一个值，快速学习算法就会根据这些权值计算在可见层已知的情况下（可见层此时的神经元要么为0要么为1，由手写体1或者2决定）每个隐层的神经元为1或者为0 的概率，此时我就得到了所有隐层神经元的值（要么为0要么为1，这是通过计算的），此时我们就知道了隐层的神经元的每个值，我们这时候把可见层当做是未知的，根据类似的求概率的方法求出可见层神经元的值或者说是重构出，此时我们的学习算法根据（暂且这样理解吧，大家到后面就知道了），得到了他们的差值，然后根据这个差值进行调整权值和偏置值（这个权值和偏置值调整不简单我们稍后讲），这就是一次权值调整了，然后我们把看做已知的，按照上面类似的求法继续求出，然后再次求出，，此时在和相减，得到误差信号，重新调整权值，然后不断的这样迭代，随着迭代的次数增加，整个系统就会达到热平衡状态，此时系统就收敛了，或者说就训练好了，我们拿一个新的手写图片1或者2从输入层输入进去就可以识别出这图片的数字了。整个学习过程就是这样，好，到这里大家一定要有这个清晰的认识，否则后面会晕的，切记，我们下面就开始正式从背景说起了：

        在诸多人工神经网络模型中，波尔兹曼机(Boltzmann Machine是Hinton和Sejnowski于1986年提出的一种根植于统计力学的随机神经网络。这种网络中的神经元是随机神经元，神经元的输出只有两种状态（未激活、激活）：一般用二进制的0和1表示，状态的取值根据概率统计法则决定。从功能上讲，BM是由随机神经元全连接组成的反馈神经网络，且对称连接，无自反馈：包含一个可见层和一个隐层的BM模型如图（a）所示。

BM具有强大的无监督学习能力，能够学习数据中复杂的规则。但是，拥有这种学习能力的代价是其训练（学习）时间非常长。此外，不仅无法确切地计算BM所表示的分布：甚至得到服从BM所表示分布的随机样本也很困难。为克服这一问题Smolensky[引入了一种限制的波尔兹曼机(Restricted Boltzman Machine , RBM)，RBM具有一个可见层，一个隐层，层内无连接，其结构如图1（b）所示。RBM具有很好的性质：在给定可见层单元状态〔输入数据）时，各隐单元的激活条件独立，反之，在给定隐单元状态时，可见层单元的激活亦条件独立。这样一来，尽管RBM所表示的分布仍无法有效计算，但通过Gibbs采样(Gibbssampling)可以得到服从RBM所表示分布的随机样本。此外：Roux和Bengio同从理论上证明，只要隐单元的数目足
够多，RBM能够拟合任意离散分布。

2006年，Hinton等人提出了一种深度信念网络(Deep BeliefNets,DBN)，并给出了该模型的一个高效学习算法。这个算法成为了其后至今深度学习算法的主要框架。在该算法中，一个DBN模型被视为由若干个RBM堆叠在一起：训练时可通过从低到高逐层训练这些RBM来实现：

       (1)   底部RBM以原始输入数据训练；

     （2）将底部RBM抽取的特征作为顶部RBM的输入训练；

     （3）过程（1）、（2）可以重复来训练所需要的尽可能多的层数。

由于RBM可以通过CD快速训练，这一框架绕过了直接从整体上训练DBN的高复杂度，从而将其化简为对多个RBM的
训练问题题。Hinton建议，经过这种方式训练后，可以再通过传统的学习算法〔如反向传播算法）对网络进行微调，从而使模型收敛到全局最优解。这种学习算法，本质上等同于先通过逐层RBM训练将模型的参数初始化为全局最优解范围附近，再通过传统学习算法进一步训练。这样一来，不仅解决了模型训练速度慢的问题，而且计算量也降低了。大量试验结果也表明，这种方式能够产生非常好的参数初始值，从而大大提升了模型的建模能力。自此，机器学习领域又产生了一个新的研究方向-----深度学习(Deep learning)，明确提出了面向人工智能的机器学习算法的设计目标。因此本节过后我们将正式进入深度学习。下面就开始深入讲解受限玻尔兹曼机，会使用大量的公式，大家做好心理准备。

受限玻尔兹曼机的基本模型

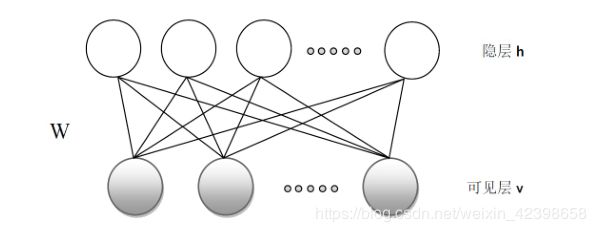
      RBM也可以被视为一个无向图(undirected graph)模型，如下图所示。为可见层，用于表示观测数据，为隐层，可视为一些特征提取器(feature detectors)，为两层之间的连接权重。Welling指出，RBM中的隐单元和可见单元可以为任意的指数族单元〔即给定隐单元(可见单元)，可见单元（隐单元）的分布可以为任意的指数族分布),如softmax单元、高斯单元、泊松单元等等。这里，为了讨论方便起见，我们假设所有的可见单元和隐单元均为二值变量，即

       如果一个RBM有n个可见单元和m个隐单元，用向量和分别表示可见单元和隐单元的状态，如上图所示，其中，表示第个可见单元的状态，与表示第个隐单元的状态。那么，对于一组给定的状态,RBM作为一个系统所具备的能量定义为：                       

上式中，是RBM的参数，他们均为实数，其中表示可见层单元 与隐单元的神经元连接权重，表示可见单元神经元的偏置（bias），表示隐层单元的偏置。当参数确定时，基于该能量函数，我们可以得到的联合概率密度分布：                      

其中为归一化因子即所有可能情况下的能量和，概率的形成就是某一个状态的能量除以总的可能状态能量和。需要解释一下的是，为什么根据能量函数就可以得到上面的式子 ，因为能量函数是符合玻尔兹曼分布的，不懂的建议查看我前面几节的基础知识，因此可以写成玻尔兹曼分布的形式，又因为是两层即可见层（输入层）和隐层，按照我们上面的学习过程，可知我们需要不断的计算这里两层的概率，又因为两层是有联系的因此需要写成联合概率密度，这个概率密度可以解释为在（其中就是待调整的权值和偏置值w，a，b）的条件下和的联合概率密度。这点需要大家理解。

           对于一个实际问题，我们关心的是由RBM所定义的关于观测数据的分布，即在训练好的权值的情况下能正确在可见层识别出内容概率的分布，如何求这个概率分布呢？很简单，对（2）式求边缘分布即可，如下：

                                      

   为了确定该分布，需要计算归一化因子 ，这需要计算次计算（因为可见单元和隐层单元他们是全连接的，又因为可见单元为n个，隐单元为m个），计算量很大，因此，即使通过训练可以得到模型的参数  ，我们任然无法计算出这些参数所确定的分布。

       但是，由于RBM的特殊结构（即层间连接，层内连接）可知：当给定可见单元的状态时，各隐单元的激活状态之间是条件独立的。此时，第j个隐单元的激活概率为：

 其中 为sigmod激活函数。

         由于RBM的结构是对称的，当给定隐单元的状态时，各可见单元的激活状态之间也是条件独立的，即第个可见单元的激活概率为：

                                                         

这里大家需对（4）、（5）两式有清晰的认识其中 、为对应的偏置值，如（4）式对隐层的某个神经元j的状态等于1的概率大小就等于把所有可见层的单元和权值相乘在相加然后加上偏置值取sigmod函数就是概率了，（5）式类似。

RBM学习算法

            学习RBM的任务是求出参数的值，大家要时刻记住，使用训练数据去训练，然后参数可以通过最大化RBM在训练集(假设包含T个样本）上的对数释然函数学习得到，即：

这里大家需要明确的是最大释然函数是做什么的，有什么样意义？这里我简单的提一下不懂的建议停下来研究一下释然函数的意义，所谓释然函数就在某些参数的情况下使其对应的概率达到最大，如上式（6）就是在参数 的情况下，使其概率概率达到最大，那么（6）式代表什么意思呢？在训练样本的情况下，我们调整参数使其最大概率的复现这个训练数据，根据我们上面的模型图我们可以知道从输入数据层（可见层）到隐层，在从隐层到可见层这是一次训练，此时的可见层的概率尽肯能的和输入时相同，就是这个目的，无线逼近样本的概率，这就是学习原则了，当有新的数据时就可以识别了。那么我们解一下释然函数为什么是这样的，这里以手写体为例，有十种手写体，我们有T个样本，我们都进可能的去复现每个样本，即每个样本是概率尽量都是最大化，因此所以的概率相乘就好了，但是乘积不容易后面的计算，又因为我们最概率的最大值这个数不感兴趣，我们只对使概率最大化的参数感兴趣，因此取对数就容易求导了，同时乘积就是求和了，最后就和（6）式一样了，上面只是简单的代表，我把上式具体化：

 其实就是把（6）式展开了，把（3）式带进去即可得到上式，我们知道是联合概率密度，而是联合概率密度的边缘密度，通过概率论我们知道，求联合概率密度的边缘密度，就是把另一个求和即可，因此上式对求和就得到了，这里大家需要理解，不理解的去查概率书籍，后面很多都是这样使用的，然后（2）（3）带进去就可以得到了，上式的最后一行是利用log的性质，即相除可以写成相减。

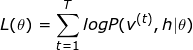 为了获得最优的参数，我们使用梯度上升进行求的最大值，其中关键步骤是计算关于各个模型参数的偏导数，下面的求导中的是代表w、a、b，因为他们的求导形式一样的，因次我们使用代替进行求导，求出后使用对于的w、a、b替换就好了，下面开始求偏导：

求偏导以前先给大家介绍一下期望的求法，如下期望的定义：

            定义  设离散型随机变量的分布律为：

                                   

             则随机变量的数学期望为记为E(X).即：

                                   

下面对对数释然函数关于求偏导可得：

                                    

上面的式子是考验大家的数学和概率基础的时候了，别害怕他，看起来很长很麻烦，其实理清思路还是很简单的，大家需要克服对数学的恐惧，拿下他你会很有成就感的，好，下面我们开始分析，首先这是对数求偏导 ，且还是对复合函数的求导，因此基本的求导大家还是懂的这些就是①式和②式他们连为一起，他们求导原理是一样的，现在我们来看看①式，大家要搞明白求和是对谁的，最外面的那个求和t=1到T的大家应该都懂，那么是求导出来相当于求期望的求和公式，那么红色中括号的乘号左边的是概率的表达式（因为分母是对所有h的能量求和而分子是其中某一个h的能量，他们相比就是概率），乘号右边的就是对应的随机变量h的能量值（这里大家需要好好理解为什么是期望，对比定义式深入理解，以后类似的就都懂了），我们知道此时①式的v是已知的情况下对h求和，因此正好符合期望公式，同时对应的分布概率为，即他求的是边缘的期望。②式求的是联合的期望，因此需要全部求和，且分布概率为，难理解的就是如何转换为求期望的，主要原因是和求期望的形式是一样的，大家好好理解①式，那个概率，是对某个隐层除上所有的隐层和不就是概率吗？而乘号后面对应的就是隐层对应的能量值，大家好好理解一下，为什么这样，自己动手推一边就出来了，好，最后我们得到③式，代表的就是均值且分别符合各自分布的均值，下面从整体介绍一下（8）式：

 其中：序表示求关于分布的数学期望。表示在可见单元限定为己知的训练样本时：隐层的概率分布，故式〔8）中的前一项比较容易计算。表示可见单元与隐单元的联合分布，由于归一化因子的存在，该分布很难取，导致我们无法直接计算式〔8）中的第二项，只能通过一些采样方法（如Gibbs采样）获取其近似值。值得指出的是，在最大化似然函数的过程中：为了加快计算速度，上述偏导数在每一迭代步中的计算一般只基于部分而非所有的训练样本进行，关于这部分内容我们将在后面讨论RBM的参数设置时详细阐述。

我们根据（1）式，以为具体参数，带进去（8）式，把（1）式拿到这里：

如果能量对 求偏导，（8）式第一项我们发现前两项为0，后面只剩下关于的参数，这时是针对概率分布来求的期望，同样第二项的结果也是只剩下关于的参数，此时是针对概率分布来的。能量函数对另外两个求偏导，可分别求得对对应的偏导，如下：

     下面，假设只有一个训练样本，我们分别用“data”和“model”来简记和这两个概率分布，则对数释然函数关于连接权重、可见层单元的偏置和隐层单元的偏置的偏导数分别为：

通过上面我们知道了学习函数，以及学习函数的难点在哪里，我们知道学习函数的难点在求均值时归一化因子 的计算量很大即整个模型的期望，计算量是,无法求解，但是我们引入了Gibbs采样解决这个问题，即我通过采样去逼近这个均值，因为分布函数我们知道。只是计算量很大，因此使用统计的方法进行处理可以很好的解决问题，这就是我们前面几节的内容就在这里用上了，但是问题是计算Gibbs采样的计算量还是很大，如下图，他需要迭代很多次才能达到热平衡状态，效率还是很低，这时候的问题是 通过Gibbs采样还是很大  怎么办呢？所以引入快速学习算法。

基于对比散度的快速学习算法

2002年，Hinton[7]提出了RBM的一个快速学习算法，即对比散度(Contrastive Divergence，CD)，与Gibbs采样不同，Hinton指出当使用训练数据初始化时，我们仅需要使用k(通常k=1)步吉布斯采样便可以得到足够好的近似。也就是本来Gibbs采样按照上面的方法需要n步迭代才能收敛，但是我现在就迭代一次，即在可见层输入数据后，计算的激活概率，然后通过在反计算可见层，此时为，然后调整权值，这就是一次迭代，做到这里以后再计算一下，这样就可以得到均值了，这就是牛逼之处了，本来需要n步迭代才能收敛，现在只需要一步迭代就可以收敛，你说牛叉不，计算量当然降低了，什么原因呢？稍后讲解。（这里需要强调的 是上图是为了大家看权值更新的过程才这样画的，但是真实的其实就两层，就是上面受限玻尔兹曼机的基本模型，只是先通过输入层（可见层）数据计算隐层值，然后把可见层看做未知的，通过隐层计算可见层，就这样不停的迭代达到热平衡状态，就可以采样了）

在CD算法一开始，可见单元的状态被设置成一个训练样本，并利用式（4）计算所有隐层单元的二值状态。在所有隐层单元的状态确定之后，根据式（5）来确定第i个可见单元取值为1的概率，进而产生可见层的一个重构(reconstruction)，这样在使用随机梯度上升法最大化对数释然函数在训练数据上的值时，各参数的更新准则为：   

其中是学习率，表示一步重构后模型定义的分布。 我们先介绍一下权值更新的伪代码，最后在介绍一步迭代的合理性。

在RBM中，可见单元数一般等于训练数据的特征维数，而隐单元数需要事先给定。为了与前文记号一致，假设可见单元数和隐单元数分别为n和m。令表示可见层与隐层间的连接权重矩阵（m×n阶),（n维列向量）和〔m维列向量）分别表示可见层与隐层的偏置向量。RBM的基于CD的快速学习算法主要步骤可描述如下：

• 输入：一个训练样本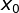；隐层神经元个数m；学习率；最大训练周期T
• 输出：连接权重矩阵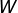、可见层的偏置向量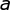、隐层的偏置向量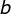
• 训练阶段：

        初始化：令可见层单元的初始状态;为随机较小的值。

        For   

                 For   (对所有隐神经元)

                           计算,即；

                            从条件分布中抽取

                   EndFor

                   For (对所有可见单元)

                             计算，即；

                             从条件分布中抽取

                    EndFor

                 

                    For   (对所有隐神经元)

                             计算,即；

                    EndFor

                  按下式更新各个参数：

                   

                    

                     

                     EndFor

这里需要和大家明确的是参数更新是按照下面的式子来的，同时简单的解释一下：

对向量的更新，输入的期望其实就是他本身数据的期望，而根据（8）式我们知道，需要在这个分布下求均值，但是这是个隐层的的分布，基本上和输入没什么关系，隐层可以单独计算输入的均值，而重构出来的就是,隐层计算矩阵即可。

对向量的更新，我们从下面的公式可以看到是求的期望，而的期望就等于=1的概率，为什么，因为要么取0，要么取1，因此1的概率和期望是相等的。

W的更新就是按照下面更新的。

 上面大家应该可以看懂的，看伪代码会发现我刚开始就是按照这个伪代码思路来讲，目的就是希望大家从整体把握他，然后在细节深入，不要思路乱了，只有你的思路很清晰的情况下，才能说深入理解，我们下面说说为什么Hinton认为一步就可以迭代成功。 

对比散度（cd）算法（Contrastive Divergence）

     什么是对比散度，大家可以自己研究一下，这里就不展开说了，我简单的说一下它有什么用，对比散度是衡量两个统计分布的相似度，和我们的相关性系数差不多，只是相关性衡量的是两个数据的相似度，而对比散度是衡量两个统计分布的相似性，有兴趣的可以自行了解一下。如果两个分布很相近，那么KL距离接近0，如果相差很远的话，KL距离很大，例如两个分布，那么二者的对比散度使用表示，下面：我根据hinton的论文解释一下为什么一步迭代就合理了：

假设，吉布斯采样的开始的概率分布为,迭代一次后分布为，不停的迭代后直到收敛我们称为：（表示和参数取值的关系），我们把和做对比散度为如下：

   同理 和也做对比散度，当然他们肯定不会为0，其中 应该是一个大点的数，而应该也是大一点的数，但是   应该比要小，因为迭代一次后接近了一点，这些还是可以接受的，现在有一个情况就是，如果我们选择了一些参数，使的 很小，可以近似为0了，说明了什么呢？说明了  ,同时也说明了此时 ，因为一旦  说明已经达到稳定了，因此会有。此时就有一个优化目标：

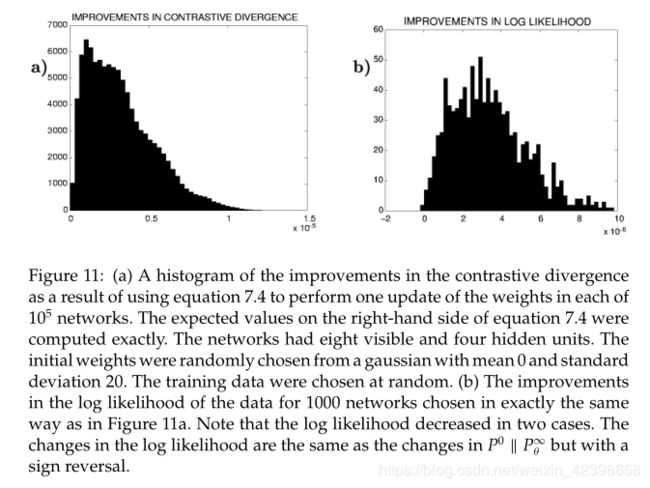
       就是说此时我使用对比散度的差值作为优化目标，找到适合的参数使的对比散度最小，因此求梯度就可以了。hinton论文里说上式的第三项可以忽略，因为值很小，给的理由有点牵强，说是根据大量数据的统计得到，可以省略，给了两图：

这里没有给出严格的数学证明，但是大家都默认可行，那就可行吧?.?

省略之后就得到了下面的式子：

上面的式子就是我们的下面的了，牛叉吧。

 目前大家都还使用这个思想。对比散度呢就是来源上面的两个散度的差，相对比。这个算法很好的解决计算量大的问题。也因此得到了广泛的应用，下一节就讲一下hinton的另一篇大作： 《Reducing the Dimensionality of Data with Neural Networks》