ArcFace(insightface)论文翻译——中英文对照+标注总结
ArcFace: Additive Angular Margin Loss for Deep Face Recognition
文章目录
- ArcFace: Additive Angular Margin Loss for Deep Face Recognition
- Abstract
- 摘要
- 1. Introduction
- 1. 介绍
- 2. Proposed Approach
- 2.1. ArcFace
- 2. 提出的方法
- 2.1. ArcFace
- 2.2. Comparison with SphereFace and CosFace
- 2.2 ArcFace与 SphereFace、CosFace 进行比较
- 2.3. Comparison with Other Losses
- 2.3. 与其他损失函数的比较
- 3. Experiments
- 3.1. Implementation Details
- 3. 实验
- 3.1. 实现细节
- 3.2. Ablation Study on Losses
- 3.2. 损失函数的研究
- 3.3. Evaluation Results
- 3.3. 结果评估(评估结果不具体翻译)
- 4. Conclusions
- 4. 结论
Abstract
One of the main challenges in feature learning using Deep Convolutional Neural Networks (DCNNs) for large-scale face recognition is the design of appropriate loss functions that enhance discriminative power. Centre loss penalises the distance between the deep features and their corresponding class centres in the Euclidean space to achieve intra-class compactness. SphereFace assumes that the linear transformation matrix in the last fully connected layer can be used as a representation of the class centres in an angular space and penalises the angles between the deep features and their corresponding weights in a multiplicative way. Recently, a popular line of research is to incorporate margins in well-established loss functions in order to maximise face class separability. In this paper, we propose an Additive Angular Margin Loss (ArcFace) to obtain highly discriminative features for face recognition. The proposed ArcFace has a clear geometric interpretation due to the exact correspondence to the geodesic distance on the hypersphere. We present arguably the most extensive experimental evaluation of all the recent state-of-the-art face recognition methods on over 10 face recognition benchmarks including a new large-scale image database with trillion level of pairs and a large-scale video dataset. We show that ArcFace consistently outperforms the state-of-the-art and can be easily implemented with negligible computational over-head. We release all refined training data, training codes,pretrained models and training logs, which will help reproduce the results in this paper.
摘要
在大规模人脸识别中,使用深度卷积神经网络(DCNNs)进行特征学习的主要挑战之一是设计适当的损失函数以增强类别之间的识别能力。Centre loss惩罚欧几里得空间中深层特征与其相应的类中心之间的距离,以实现类内紧凑性。SphereFace假设最后一个完全连接层中的线性变换矩阵可以表示角度空间中类别的中心,并以乘法的方式惩罚深度特征与其相应权重之间的角度。最近,一个流行的研究领域是将裕度纳入已建立的损失函数中,以最大限度地提高人脸类别的可分性。在本文中,我们提出了一种附加角度裕度的损失函数(ArcFace),以获得人脸识别的高度可分别特征。由于与超球面测量距离的精确对应,本文提出的ArcFace有清晰的几何解释。我们提出了最广泛的实验在超过10个人脸识别基准上评估了最新所有的state-of-the-art 人脸识别方法,包括一个新的大型图像数据库万亿级的图像对和一个大规模的视频数据集。我们表明,ArcFace始终优于最先进的技术,并且可以很容易地用可忽略不计的计算成本来实现。我们发布了所有经过改进的训练数据、训练代码、预训练模型和训练日志,这将有助于重现本文的结果。
注:
1. 大规模人脸识别中使用DCNNs进行特征学习的主要挑战之一是设计适当的损失函数以增强类别之间的识别能力。
2.最近流行的研究是将裕度纳入已建立的损失函数中,以最大限度地提高人脸类别的可分性。
3.由于与超球面测量距离的精确对应,ArcFace有清晰的几何解释。
1. Introduction
Face representation using Deep Convolutional Neural Network (DCNN) embedding is the method of choice for face recognition [30, 31, 27, 22]. DCNNs map the face image, typically after a pose normalisation step [42], into a feature that has small intra-class and large inter-class distance.

1. 介绍
使用深度卷积神经网络(DCNNs)嵌入来表示人脸是人脸识别的首选方法[30,31,27,22]。DCNNs将人脸图像(通常在归一化步骤[42]之后)映射到具有较小类内距离和较大类间距离的特征空间中。
There are two main lines of research to train DCNNs for face recognition. Those that train a multi-class classifier which can separate different identities in the training set, such by using a softmax classifier [31, 22, 5], and those that learn directly an embedding, such as the triplet loss [27]. Based on the large-scale training data and the elaborate DCNN architectures, both the softmax-loss-based methods [5] and the triplet-loss-based methods [27] can obtain excellent performance on face recognition. However,both the softmax loss and the triplet loss have some draw-backs. For the softmax loss: (1) the size of the linear transformation matrix W ∈ R d×n increases linearly with the identities number n; (2) the learned features are separable for the closed-set classification problem but not discriminative enough for the open-set face recognition problem. For the triplet loss: (1) there is a combinatorial explosion in the number of face triplets especially for large-scale datasets, leading to a significant increase in the number of iteration steps; (2) semi-hard sample mining is a quite difficult problem for effective model training.
训练用于人脸识别的DCNNs有两个主要的研究方向。训练一个多类别分类器,它可以在训练集中分离不同的身份,例如使用一个Softmax分类器[31,22,5],还有直接学习嵌入特征,例如 triplet loss[27]。基于大规模训练数据集和复杂的DCNN结构,基于softmax loss的方法[5]和triplet loss的方法[27]都可以获得良好的人脸识别性能。然而,softmax loss损失和triplet loss都有一定的缺点。对于Softmax loss:(1)线性变换矩阵 W ∈ r d × n W∈r^{d×n} W∈rd×n的大小随着身份数量n的增加而线性增大;(2)对于closed-set 分类问题,所学习的特征是可分离的,但对于open-set人脸识别问题,识别性不够。对于triplet loss:(1)人脸三元组的数量出现爆炸式增长,特别是对于大型数据集,导致迭代次数显著增加;(2)样本挖掘策略造成很难有效的进行模型的训练。
Several variants [36, 8, 43, 17, 35, 33, 6, 32, 25] have been proposed to enhance the discriminative power of the softmax loss. Wen et al. [36] pioneered the centre loss, the Euclidean distance between each feature vector and its class centre, to obtain intra-class compactness while the inter-class dispersion is guaranteed by the joint penalisation of the softmax loss. Nevertheless, updating the actual centres during training is extremely difficult as the number of face classes available for training has recently dramatically increased.
已经提出了几种变体[36、8、43、17、35、33、6、32、25]来增强Softmax loss的识别能力。[36]提出了centre loss,即每个特征向量与其类别中心之间的欧几里得距离,以获得类内紧度,而类间分散则由Softmax loss 的联合惩罚来保证。然而,在训练期间更新实际类别中心非常困难,因为可供训练的人脸类别数量最近急剧增加。
By observing that the weights from the last fully connected layer of a classification DCNN trained on the softmax loss bear conceptual similarities with the centres of each face class, the works in [17, 18] proposed a multiplicative angular margin penalty to enforce extra intra-class compactness and inter-class discrepancy simultaneously, leading to a better discriminative power of the trained model.Even though Sphereface [17] introduced the important idea of angular margin, their loss function required a series of approximations in order to be computed, which resulted in an unstable training of the network. In order to stabilise training, they proposed a hybrid loss function which includes the standard softmax loss. Empirically, the softmax loss dominates the training process, because the integer-based multiplicative angular margin makes the target logit curve very precipitous and thus hinders convergence. CosFace [35, 33] directly adds cosine margin penalty to the target logit, which obtains better performance compared to SphereFace but admits much easier implementation and relieves the need for joint supervision from the softmax loss.
通过观察,发现通过Softmax loss 训练的分类DCNN最后一个完全连接层的权重与每个人脸类别的中心具有概念上的相似性,在[17,18]中提出了一个乘法角度裕度惩罚,以同时加强类内紧度和类间差异,从而提高了训练模型的识别能力。尽管Sphereface[17]引入了角度裕度的重要概念,但它的损失函数需要一系列近似才能计算出来,从而导致网络训练不稳定。为了稳定训练,他们提出了一个混合损失函数,其中包括标准的Softmax loss。经验上,softmax loss 在训练过程中占主导地位,因为基于整数的乘角裕度使得目标逻辑曲线非常陡峭,从而阻碍了收敛。CosFace[35,33]直接将cosine裕度惩罚添加到目标逻辑回归中,与SphereFace相比,它获得了更好的性能,但更容易的实现,减少了softmax loss 联合监督的需要。
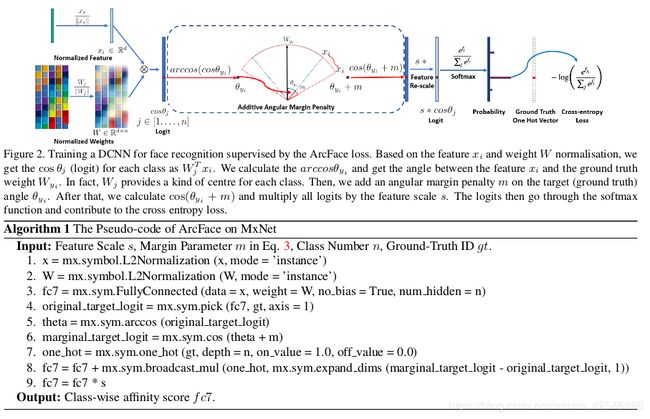
In this paper, we propose an Additive Angular Margin Loss (ArcFace) to further improve the discriminative power of the face recognition model and to stabilise the training process. As illustrated in Figure 2, the dot product between the DCNN feature and the last fully connected layer is equal to the cosine distance after feature and weight normalisation. We utilise the arc-cosine function to calculate the angle between the current feature and the target weight. Afterwards, we add an additive angular margin to the target angle, and we get the target logit back again by the cosine function. Then, we re-scale all logits by a fixed feature norm, and the subsequent steps are exactly the same as in the softmax loss. The advantages of the proposed ArcFace can be summarised as follows:
Engaging. ArcFace directly optimises the geodesic distance margin by virtue of the exact correspondence between
the angle and arc in the normalised hypersphere. We intuitively illustrate what happens in the 512-D space via analysing the angle statistics between features and weights.
Effective. ArcFace achieves state-of-the-art performance on ten face recognition benchmarks including large-scale
image and video datasets.
Easy. ArcFace only needs several lines of code as given in Algorithm 1 and is extremely easy to implement in the
computational-graph-based deep learning frameworks, e.g. MxNet [7], Pytorch [23] and Tensorflow [4]. Furthermore,
contrary to the works in [17, 18], ArcFace does not need to be combined with other loss functions in order to have
stable performance, and can easily converge on any training datasets.
Efficient. ArcFace only adds negligible computational complexity during training. Current GPUs can easily support millions of identities for training and the model parallel strategy can easily support many more identities.
为了进一步提高人脸识别模型的识别能力,稳定训练过程,本文提出了一种加性角度裕量损失算法。如图2所示,DCNN特征和最后一个完全连接层之间的点积等于特征和权重归一化后的余弦距离。我们利用arc-cosine函数来计算当前特征和目标权重之间的角度。然后,在目标角上加上一个附加的角度裕度,用余弦函数重新计算逻辑回归的反向传播过程。然后,我们用一个固定的特征范数重新缩放所有的逻辑,随后的步骤与Softmax loss 中的步骤完全相同。所所提出的ArcFace的优点可以总结如下:
吸引人的 ArcFace 直接优化测量距离裕度,因为归一化超球体中的角和弧度的对应。我们通过分析特征和权重之间的角度统计,直观地说明512-D空间中的情况。
有效 Arcface在10个人脸识别基准上实现了state-of-the-art的性能,包括大规模图像和视频数据集。
容易 Arcface只需要算法1中给出的几行代码,并且非常容易在基于计算图的深度学习框架上实现,例如MXnet[7]、Pythort[23]和TensorFlow[4]。此外,与[17,18]中的工作相比,为了性能的稳定,ArcFace不需要与其他loss函数实现联合监督,可以很容易地收敛于任何训练数据集。
高效 在训练过程中,Arcface只增加了可忽略的计算复杂性。当前的GPU可以轻松支持数百万个身份训练,模型并行策略可以轻松支持更多的身份。
注:
1. 人脸识别的DCNNs有两个主要的研究方向:分类学习(softmax loss)、度量学习(triplet loss),同时提出两种loss的缺点。
2.提出了几种变体,但都有缺点。
3.通过观察权重与类中心的关系提出Sphereface,而且引入了角度裕度的重要概念,但其需要一些近似的计算从而导致训练不稳定。
4. 提出了Arcface的优点,谈及的可以说很优雅了。
2. Proposed Approach
2.1. ArcFace
The most widely used classification loss function, softmax loss, is presented as follows:
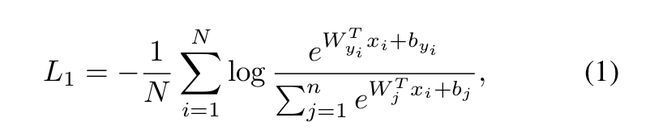
where x i ∈ R d denotes the deep feature of the i-th sample, belonging to the y i -th class. The embedding feature dimension d is set to 512 in this paper following [36, 43, 17, 35].W j ∈ R d denotes the j-th column of the weight W ∈ R d×n and b j ∈ R n is the bias term. The batch size and the class number are N and n, respectively. Traditional softmax loss is widely used in deep face recognition [22, 5]. However,the softmax loss function does not explicitly optimise the feature embedding to enforce higher similarity for intra-class samples and diversity for inter-class samples, which results in a performance gap for deep face recognition under large intra-class appearance variations (e.g. pose variations [28, 44] and age gaps [20, 45]) and large-scale test scenarios (e.g. million [14, 37, 19] or trillion pairs [3]).
2. 提出的方法
2.1. ArcFace
最广泛使用的分类损失函数Softmax Loss如下所示:
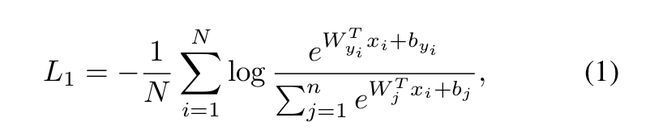
式中, x i ∈ R d x_i∈R^d xi∈Rd表示第i个样本的深层特征,属于 y i y_i yi类。本文将嵌入特征维数d设为512,遵循[36,43,17,35], W j ∈ R d W_j∈R^d Wj∈Rd表示权重 W ∈ R d ∗ n W∈R^{d*n} W∈Rd∗n的 j j j列, b j ∈ R n b_j∈R^n bj∈Rn为偏置项。批次大小和类别号分别为N和n。传统的Softmax loss 在人脸识别中得到了广泛应用[22,5]。然而,Softmax loss 函数并没有明确地优化特征嵌入,以增强类内样本的相似度和类间样本多样性,这导致在较大的类内外观变化(例如姿势变化[28,44]和年龄差异[20,45])和较大规模测试场景,深层人脸识别的性能存在差异。(例如百万对[14,37,19]或万亿对[3])。
For simplicity, we fix the bias b j = 0 as in [17]. Then, we transform the logit [24] as W j T x i = kW j k kx i k cos θ j , where θ j is the angle between the weight W j and the feature x i . Following [17, 35, 34], we fix the individual weightn kW j k = 1 by l 2 normalisation. Following [26, 35, 34, 33], we also fix the embedding feature kx i k by l 2 normalisation and rescale it to s. The normalisation step on features andweights makes the predictions only depend on the angle between the feature and the weight. The learned embedding features are thus distributed on a hypersphere with a radius of s.
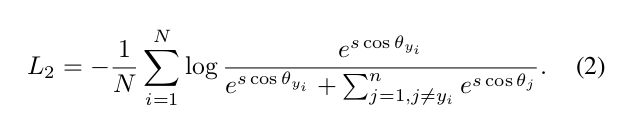
为了简单起见,我们修正了偏差 b j = 0 b_j=0 bj=0,如[17]所示。然后,我们将逻辑表达式[24]转换为 W j T x i = ∣ ∣ W j ∣ ∣ ∣ ∣ x i ∣ ∣ c o s θ j W_j^Tx_i=||W_j||||x_i|| cosθ_j WjTxi=∣∣Wj∣∣∣∣xi∣∣cosθj,其中 θ j θ_j θj是权 W j W_j Wj与特征 x i x_i xi之间的角度。遵循[17,35,34],我们通过L2归一化来修正单个权重 ∣ ∣ W j ∣ ∣ = 1 ||W_j||=1 ∣∣Wj∣∣=1。遵循[26,35,34,33],我们还通过L2归一化来固定嵌入特征 ∣ ∣ x i ∣ ∣ ||x_i|| ∣∣xi∣∣,并将其重新缩放成s。特征和权重的归一化步骤使预测仅取决于特征和权重之间的角度。因此,所学的嵌入特征分布在半径为s的超球体上。
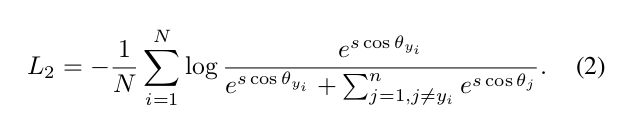
As the embedding features are distributed around each feature centre on the hypersphere, we add an additive angular margin penalty m between x i and W y i to simultaneously enhance the intra-class compactness and inter-class discrepancy. Since the proposed additive angular margin penalty is equal to the geodesic distance margin penalty in the normalised hypersphere, we name our method as ArcFace.
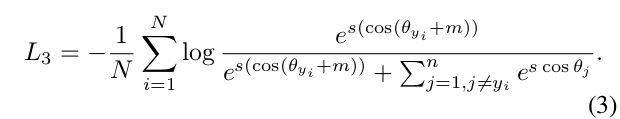
由于嵌入特征分布在超球面上的每个特征中心的周围,我们在 x i x_i xi和 W y i W_{y_i} Wyi之间增加了一个附加的角度缘惩罚m,从而同时增强了类内紧度和类间差异。由于所提出的加性角度裕度惩罚等于规范化超球体中的测量距离裕度惩罚,因此我们将此方法命名为ArcFace。
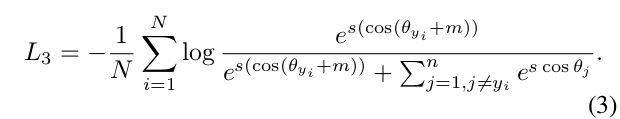
We select face images from 8 different identities containing enough samples (around 1,500 images/class) to train 2D feature embedding networks with the softmax and ArcFace loss, respectively. As illustrated in Figure 3, the softmax loss provides roughly separable feature embedding but produces noticeable ambiguity in decision boundaries, while the proposed ArcFace loss can obviously enforce a more evident gap between the nearest classes.

我们从8个包含足够样本(大约1500个图像/类)的不同身份中选择人脸图像,分别训练具有Softmax loss和ArcFace loss 的二维特征嵌入网络。如图3所示,Softmax loss 提供了大致可分离的特征嵌入,但在决策边界中会产生明显的模糊性,而所提出的ArcFace loss 显然会在最近的类之间产生更明显的差距。

注:
1. 说明了由softmax loss推出ArcFace的过程。
2.并做了个实验来对比softmax loss推出ArcFace loss的效果。
2.2. Comparison with SphereFace and CosFace
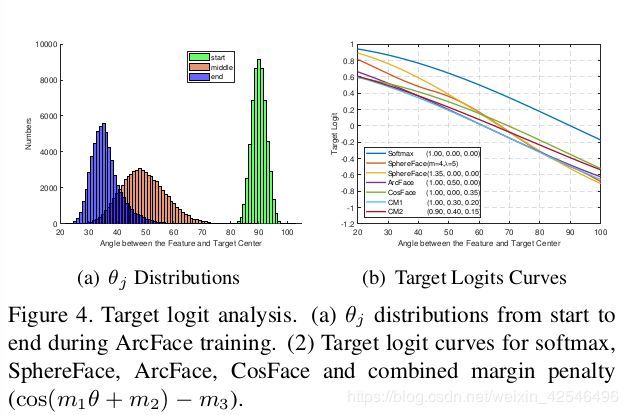
Numerical Similarity. In SphereFace [17, 18], ArcFace, and CosFace [35, 33], three different kinds of margin penalty are proposed, e.g. multiplicative angular margin m 1 , additive angular margin m 2 , and additive cosine margin m 3 , respectively. From the view of numerical analysis, different margin penalties, no matter add on the angle [17] or cosine space [35], all enforce the intra-class compactness and inter-class diversity by penalising the target logit [24].In Figure 4(b), we plot the target logit curves of SphereFace, ArcFace and CosFace under their best margin settings. We only show these target logit curves within [20 ◦ , 100 ◦ ] because the angles between W y i and x i start from around 90 ◦ (random initialisation) and end at around 30 ◦ during Arc-Face training as shown in Figure 4(a). Intuitively, there are three factors in the target logit curves that affect the performance, i.e. the starting point, the end point and the slope.
2.2 ArcFace与 SphereFace、CosFace 进行比较
数值相似性 在SphereFace[17,18]、ArcFace和CosFace[35,33]中,提出了三种不同的裕度惩罚,分别是乘法角度裕度 m 1 m_1 m1加法角度裕度 m 2 m_2 m2和加法余弦裕度 m 3 m_3 m3。从数值分析的角度来看,不同的裕度惩罚,无论是加上角度[17]还是加在余弦空间[35],都通过惩罚目标逻辑来加强类内紧度和类间多样性[24],在图4(b)中,我们绘制了在其最佳裕度设置下的SphereFace、ArcFace和CosFace的目标逻辑曲线。我们只在[ 2 0 。 20 ^。 20。, 10 0 。 100^。 100。]内显示这些目标逻辑曲线,因为 W y i Wy_i Wyi和 x i x_i xi之间的角度从大约 9 0 。 90 ^。 90。(随机初始化)开始,在ArcFace训练期间在大约 3 0 。 30 ^。 30。结束,如图4(a)所示。直观地说,目标逻辑曲线中有三个影响性能的因素,即起点、终点和坡度。

By combining all of the margin penalties, we implement SphereFace, ArcFace and CosFace in an united framework
with m 1 , m 2 and m 3 as the hyper-parameters.
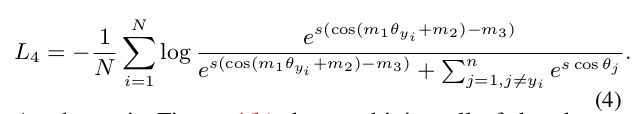
As shown in Figure 4(b), by combining all of the above-motioned margins (cos(m 1 θ + m 2 ) − m 3 ), we can easily get some other target logit curves which also have high performance.
通过合并所有的裕度惩罚,在统一框架下我们实现了结合 m 1 m_1 m1、 m 2 m_2 m2和 m 3 m_3 m3超参数的裕度惩罚。
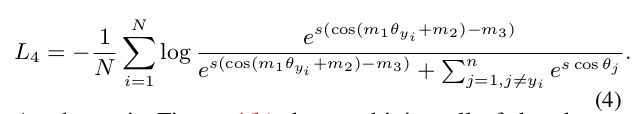
如图4(b)所示,通过将上述所有的裕度结合起来 ( c o s ( m 1 θ + m 2 ) − m 3 ) (cos(m_1θ+m_2)−m_3) (cos(m1θ+m2)−m3),我们可以很容易地得到其他一些同样具有高性能的目标逻辑曲线。
Geometric Difference. Despite the numerical similarity between ArcFace and previous works, the proposed ad-ditive angular margin has a better geometric attribute as the angular margin has the exact correspondence to the geodesic distance. As illustrated in Figure 5, we compare the decision boundaries under the binary classification case. The proposed ArcFace has a constant linear angular margin throughout the whole interval. By contrast, SphereFace and CosFace only have a nonlinear angular margin.
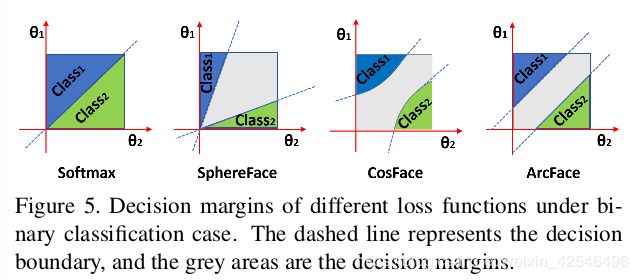
几何差异 尽管ArcFace与以往的工作相似,但由于角度与测量距离具有精确的对应关系,提出的加性角度裕度具有较好的几何属性。如图5所示,我们比较了二分类情况下的决策边界。所提出的ArcFace在整个区间内具有恒定的线性角度裕度。相比之下,SphereFace和CosFace只有一个非线性的角度裕度。

The minor difference in margin designs can have “butterfly effect” on the model training. For example, the original SphereFace [17] employs an annealing optimisation strategy. To avoid divergence at the beginning of training, joint
supervision from softmax is used in SphereFace to weaken the multiplicative margin penalty. We implement a new version of SphereFace without the integer requirement on the margin by employing the arc-cosine function instead of using the complex double angle formula. In our implementation, we find that m = 1.35 can obtain similar performance compared to the original SphereFace without any convergence difficulty
裕度设计的微小差异可能对模型训练产生“蝴蝶效应”。例如,原始SphereFace[17]采用退火优化策略。为了避免训练开始时出现差错,在SphereFac上采用了Softmax的联合监督,以削弱乘法边缘惩罚。采用arc-cosine函数代替复杂的双角度公式,实现了一种新的无整数要求SphereFace。在我们的实现中,我们发现m=1.35可以获得与SphereFace相似的性能,而不存在任何收敛困难。
注:
1. ArcFace与 SphereFace、CosFace 进行比较。
2.对ArcFace与 SphereFace、CosFace 裕度取不同值时的性能进行了比较。
3.将三种裕度整合到一起。
4. 利用二分类来对ArcFace与 SphereFace、CosFace 的决策边界进行比较。
2.3. Comparison with Other Losses
Other loss functions can be designed based on the angular representation of features and weight-vectors. For examples, we can design a loss to enforce intra-class compactness and inter-class discrepancy on the hypersphere. As shown in Figure 1, we compare with three other losses in this paper.
Intra-Loss is designed to improve the intra-class compactness by decreasing the angle/arc between the sample and the ground truth centre.

2.3. 与其他损失函数的比较
其他损失函数可以根据特征和权重向量的角度表示来设计。例如,我们可以设计一个损失来加强超球面上的类内紧性和类间差异。如图1所示,我们在本文中比较了三种损失函数。
类内损失旨在通过减小样本与真实类别中心之间的角度/弧来提高类内紧密性。

Inter-Loss targets at enhancing inter-class discrepancy by increasing the angle/arc between different centres.
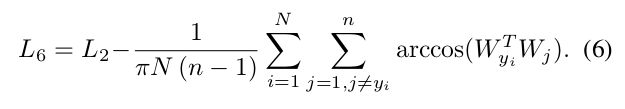
The Inter-Loss here is a special case of the Minimum Hyper-spherical Energy (MHE) method [16]. In [16], both
hidden layers and output layers are regularised by MHE. In the MHE paper, a special case of loss function was also proposed by combining the SphereFace loss with MHE loss on the last layer of the network.
Triplet-loss aims at enlarging the angle/arc margin between triplet samples. In FaceNet [27], Euclidean margin is applied on the normalised features. Here, we employ the triplet-loss by the angular representation of our features as neg arccos(x pos x i ).
类内损失的目标是通过增加不同中心之间的角度/弧来增强类间差异。
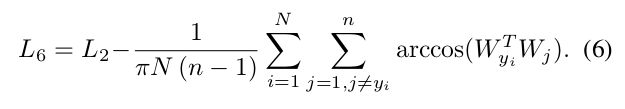
这里的内部损失是最小超球面能量(MHE)法的一个特例[16]。在[16]中隐藏层和输出层都由MHE调整。在[16]还提出了一种特殊情况下的损失函数,将网络最后一层的SphereFace loss和MHE loss相结合。
三元组损失旨在扩大三元样品之间的角度/弧裕度。在FaceNet[27]中,欧几里得边缘应用于归一化特征。在这里,我们利用的角度裕度来表示三重损失arccos( x i p o s x i x_i^{pos}x_i xiposxi)+ m m m ≤ ≤ ≤ a r c c o s ( x i n e g x i ) arccos(x_i^{neg}x_i) arccos(xinegxi)。
3. Experiments
3.1. Implementation Details
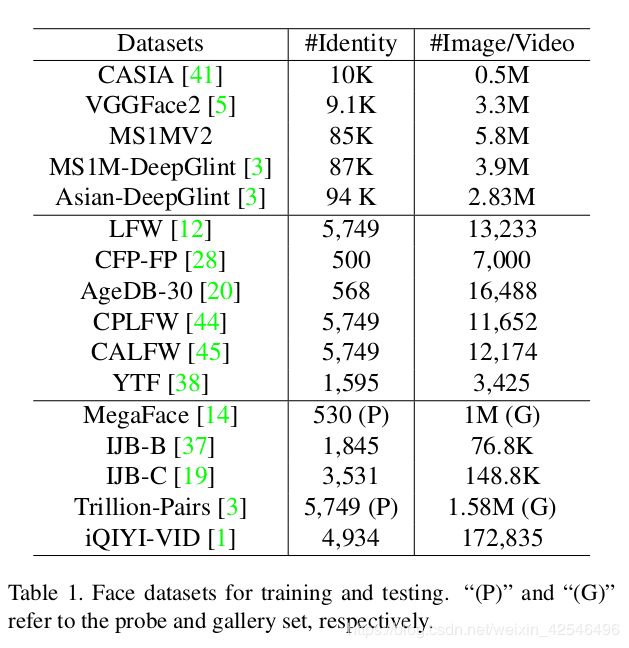
Datasets. As given in Table 1, we separately employ CASIA [41], VGGFace2 [5], MS1MV2 and DeepGlint-Face (including MS1M-DeepGlint and Asian-DeepGlint) [3] as our training data in order to conduct fair comparison with other methods. Please note that the proposed MS1MV2 is a semi-automatic refined version of the MS-Celeb-1M dataset [9]. To best of our knowledge, we are the first to employ ethnicity-specific annotators for large-scale face image annotations, as the boundary cases (e.g. hard samples and noisy samples) are very hard to distinguish if the annotator is not familiar with the identity. During training, we explore efficient face verification datasets (e.g. LFW [12], CFP-FP [28], AgeDB-30 [20]) to check the improvement from different settings. Besides the most widely used LFW [12] and YTF [38] datasets, we also report the performance of ArcFace on the recent large-pose and large-age datasets(e.g. CPLFW [44] and CALFW [45]). We also extensively test the proposed ArcFace on large-scale image datasets (e.g.MegaFace [14], IJB-B [37], IJB-C [19] and Trillion-Pairs [3]) and video datasets (iQIYI-VID [1]).
3. 实验
3.1. 实现细节
数据集 如表1所示,我们分别采用CASIA[41]、VGGFACE2[5]、MS1MV2和DeepGlint-Face(包括MS1M-Deepglin和Asian-Deepglin)[3]作为我们的训练数据集,以便与其他方法进行公平比较。请注意,建议MS1MV2是MS-CELEB-1M数据集的半自动优化版本[9]。据我们所知,我们是第一个使用特定于种族的注释器进行大规模人脸图像注释的人,因为边界情况(例如硬样本和噪声样本)很难区分注释器是否不熟悉其身份。在训练过程中,我们探索了有效的人脸验证数据集(如LFW[12]、CFP-FP[28]、AGEDB-30[20]),以对不同设置进行改进。除了最广泛使用的LFW[12]和YTF[38]数据集,我们还报告了Arcface在最近的大姿态和大年龄数据集(如CPLFW[44]和CALFW[45])上的性能。我们还广泛地在大规模图像数据集(例如MegaFace [14], IJB-B [37], IJB-C [19]和Trillion-Pairs[3])和视频数据集(iQIYI-VID [1])上测试所提出的ArcFace。

Experimental Settings. For data prepossessing, we follow the recent papers [17, 35] to generate the normalised face crops (112 × 112) by utilising five facial points. For the embedding network, we employ the widely used CNN architectures, ResNet50 and ResNet100 [11, 10]. After the last convolutional layer, we explore the BN [13]-Dropout [29]-FC-BN structure to get the final 512-D embedding feature. In this paper, we use ([training dataset, network structure, loss]) to facilitate understanding of the experimental settings.
实验设置 对于数据预处理,我们按照最近的论文[17,35]通过使用五个面部关键点生成归一化的面部裁剪图像(112×112)。对于嵌入网络,我们采用了广泛使用的CNN架构,ResNet50 和ResNet100 [11, 10]。在最后一个卷积层之后,我们探索了BN[13]-Dropout [29]-FC-BN结构,得到了最终的512-D嵌入特性。在本文中,我们使用([训练数据集,网络结构,损失])来帮助理解实验设置。
We follow [35] to set the feature scale s to 64 and choose the angular margin m of ArcFace at 0.5. All experiments in this paper are implemented by MXNet [7]. We set the batch size to 512 and train models on four NVIDIA Tesla P40 (24GB) GPUs. On CASIA, the learning rate starts from 0.1 and is divided by 10 at 20K, 28K iterations. The training process is finished at 32K iterations. On MS1MV2, we divide the learning rate at 100K,160K iterations and finish at 180K iterations. We set momentum to 0.9 and weight decay to 5e − 4. During testing, we only keep the feature embedding network without the fully connected layer (160MB for ResNet50 and 250MB for ResNet100) and extract the 512-D features (8.9 ms/face for ResNet50 and 15.4 ms/face for ResNet100) for each normalised face. To get the embedding features for templates (e.g. IJB-B and IJB-C) or videos (e.g. YTF and iQIYI-VID), we simply calculate the feature centre of all images from the template or all frames from the video. Note that, overlap identities between the training set and the test set are removed for strict evaluations, and we only use a single crop for all testing.
我们按照[35]将特征比例s设置为64,并选择角度间隔m为0.5。本文中的所有实验都是由mxnet[7]实现的。我们将批量大小设置为512,并在四个Nvidia Tesla P40(24GB)GPU上训练。在CASIA上,学习率从0.1开始,在20k,28k迭代时除以10。训练过程在32K迭代时完成。在MS1Mv2上,我们将学习速率划分为100k、160k次迭代,并在180k次时迭代完成。我们将动量设置为0.9,重量衰减为5e-4。在测试过程中,我们只保留没有完全连接层的特征嵌入网络(resnet50为160MB,resnet100为250MB),并为每个归一化的人脸提取512维度的特征(resnet50为8.9ms/面,resnet100为15.4ms/面)。为了获得模板(如ijb-b和ijb-c)或视频(如ytf和iqiyi-vid)的嵌入特征,我们只需计算来自模板所有图像或视频中所有帧的特征中心 。注意,为了进行严格的评估将删除训练集和测试集之间的重叠标识并且我们只对所有测试使用一个裁剪。
注:
1. 训练数据集与验证数据集的介绍。
2.预处理方法、网络定义、使用mxnet框架,一些训练策略的介绍。
3.训练硬件设置,训练超参数设置s=64/m=0.5,训练数据集预处理。
3.2. Ablation Study on Losses
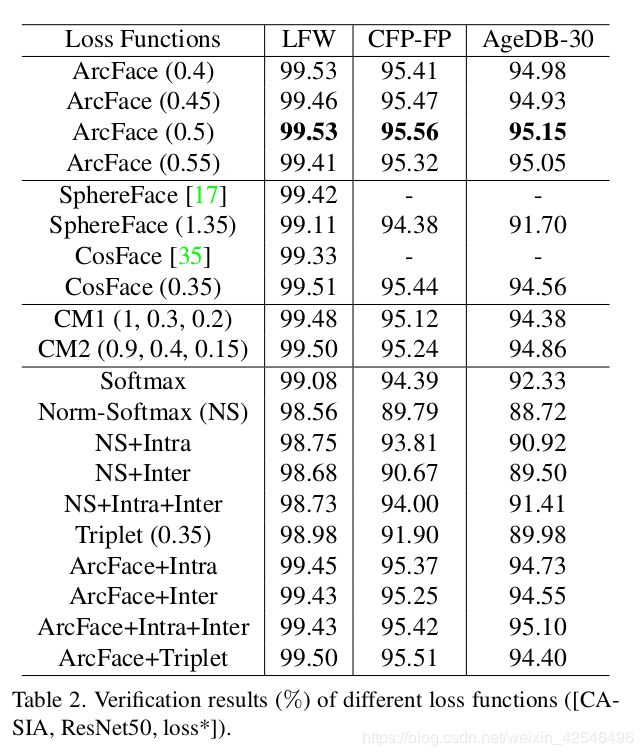
In Table 2, we first explore the angular margin setting for ArcFace on the CASIA dataset with ResNet50. The best margin observed in our experiments was 0.5. Using the proposed combined margin framework in Eq. 4, it is easier to set the margin of SphereFace and CosFace which we found to have optimal performance when setting at 1.35 and 0.35, respectively. Our implementations for both SphereFace and CosFace can lead to excellent performance without observing any difficulty in convergence. The proposed ArcFace achieves the highest verification accuracy on all three test sets. In addition, we performed extensive experiments with the combined margin framework (some of the best performance was observed for CM1 (1, 0.3, 0.2) and CM2 (0.9, 0.4, 0.15)) guided by the target logit curves in Figure 4(b). The combined margin framework led to better performance than individual SphereFace and CosFace but upper-bounded by the performance of ArcFace.
3.2. 损失函数的研究
在表2中,我们首先探讨了使用ResNet50在CASIA数据集上ArcFace的角度裕度设置。实验中观察到的最佳裕度为0.5。利用公式4中提出的组合裕度框架,可以更容易地设置SphereFace和CosFace的裕度,我们发现当分别设置为1.35和0.35时性能最佳。我们对SphereFace 和CosFace的实现获得了出色的性能但没有遇到任何收敛方面的困难。提出的ArcFace在所有三个测试集上都达到了最高的验证精度。此外,我们在图4(b)中的目标逻辑曲线指导下,对组合裕度框架进行了大量实验(观察到CM1(1,0.3,0.2)和CM2(0.9,0.4,0.15)时性能最佳)。组合裕度框架比单个SphereFace和CosFace框架具有更好的性能,但其上限是ArcFace的性能。
Besides the comparison with margin-based methods, we conduct a further comparison between ArcFace and other losses which aim at enforcing intra-class compactness (Eq. 5) and inter-class discrepancy (Eq. 6). As the baseline we have chosen the softmax loss and we have observed performance drop on CFP-FP and AgeDB-30 after weight and feature normalisation. By combining the softmax with the intra-class loss, the performance improves on CFP-FP and AgeDB-30. However, combining the softmax with the inter-class loss only slightly improves the accuracy. The fact that Triplet-loss outperforms Norm-Softmax loss indicates the importance of margin in improving the performance. However, employing margin penalty within triplet samples is less effective than inserting margin between samples and centres as in ArcFace. Finally, we incorporate the Intra-loss, Inter-loss and Triplet-loss into ArcFace, but no improvement is observed, which leads us to believe that Ar-cFace is already enforcing intra-class compactness, inter-class discrepancy and classification margin.
除了与基于裕度的方法进行比较外,我们还进一步比较了Arcface和其他旨在增强类内紧凑性(等式5)和类间差异(等式6)的损失。作为基线,我们选择了Softmax loss,并观察到在权重和特征归一化后在CFP-FP和AGEDB-30的性能下降。通过将Softmax与类内损失相结合,提高了CFP-FP和AGEDB-30的性能。但是,将Softmax与类间损失相结合只会稍微提高精度。三元组损失优于Norm-Softmax loss这一事实表明,裕度对提高性能的重要性。然而,在三重样本中使用裕度惩罚比在样本和中心之间插入裕度效果差。 最后,我们将内部损失和三元损失合并到Arcface中,但没有观察到任何改进,这使我们相信,AecFace已经增强了类内的紧凑性、类间的差异性。
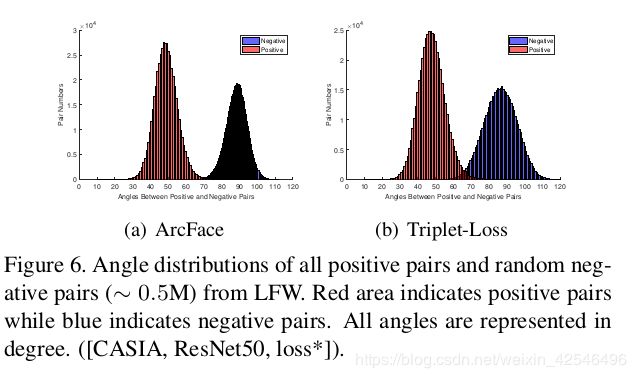
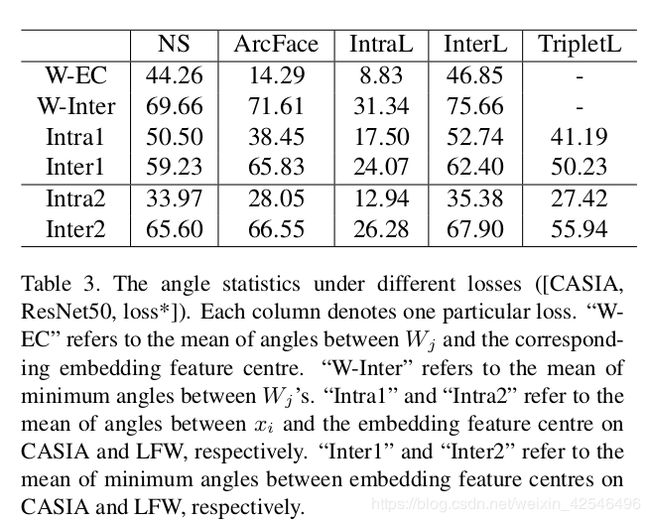
To get a better understanding of ArcFace’s superiority,we give the detailed angle statistics on training data (CASIA) and test data (LFW) under different losses in Table3. We find that (1) W j is nearly synchronised with embedding feature centre for ArcFace (14.29 ◦ ), but there is an obvious deviation (44.26 ◦ ) between W j and the em-bedding feature centre for Norm-Softmax. Therefore, the angles between W j cannot absolutely represent the interclass discrepancy on training data. Alternatively, the embedding feature centres calculated by the trained network are more representative. (2) Intra-Loss can effectively compress intra-class variations but also brings in smaller inter-class angles. (3) Inter-Loss can slightly increase inter-class discrepancy on both W (directly) and the embedding network (indirectly), but also raises intra-class angles. (4) ArcFace already has very good intra-class compactness and inter-class discrepancy. (5) Triplet-Loss has similar intra-class compactness but inferior inter-class discrepancy compared to ArcFace. In addition, ArcFace has a more distinct margin than Triplet-Loss on the test set as illustrated in Figure 6.
为了更好地理解ArcFace的优越性,我们在表3中给出了不同损失情况下训练数据集(CASIA)和测试数据集(LFW)的详细角度统计。我们发现:(1) W j W_j Wj与ArcFace嵌入特征的中心几乎同步( 14.2 9 。 14.29^。 14.29。),但在 W j W_j Wj与标准Softmax 嵌入特征中心之间存在明显的偏差( 44.2 6 。 44.26^。 44.26。)。因此, W j W_j Wj之间的夹角不能完全代表训练数据的类间差异。或者,由训练网络计算的嵌入特征中心更具代表性。(2)内部损失可以有效压缩类内变化,但也会带来较小的类间角度。(3)类间损失可以略微增加W(直接)和嵌入网络(间接)上的类间差异,但也会增加类内角度。(4)ArcFace已经具有很好的类内紧凑性和类间差异性。(5)与ArcFace相比,三元损失具有相似的类内紧度,但类间差较低。此外,如图6所示,Arcface比测试集的三元损失有更明显的裕度。
注:
1. 组合裕度相关参数的设置,最好性能比SphereFace和CosFace框架更好但上限是ArcFace。
2.比较了Arcface与其他可以减小类内间距加大类间距离的损失函数进行对比,结果表示Arcface已经增强了类内的紧凑性、类间的差异性。
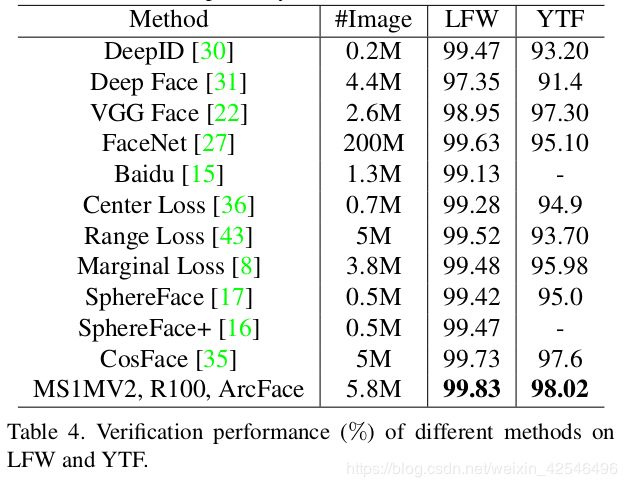
3.3. Evaluation Results
3.3. 结果评估(评估结果不具体翻译)
4. Conclusions
In this paper, we proposed an Additive Angular Margin Loss function, which can effectively enhance the discriminative power of feature embeddings learned via DCNNs for face recognition. In the most comprehensive experiments reported in the literature we demonstrate that our method consistently outperforms the state-of-the-art. Code and details will provided publicly available.
4. 结论
本文提出了一种加性角度裕度损失函数,它可以有效地提高通过DCNNs学习的特征嵌入在人脸识别中的识别能力。在文献阐述的实验中,我们证明我们的方法始终优于最先进的方法。代码和细节已开源。