2020-2-14 深度学习笔记7 - 深度学习中的正则化4（稀疏表示-稀疏化激活单元(元素稀疏)，Bagging和其他集成方法，Dropout-廉价Bagging近似）

第七章 深度学习中的正则化

官网链接
2020-2-9 深度学习笔记7 - 深度学习中的正则化1（参数范数惩罚和范数惩罚约束）
2020-2-12 深度学习笔记7 - 深度学习中的正则化2（欠约束，数据集增强，噪声鲁棒性，输出目标注入噪声）
2020-2-13 深度学习笔记7 - 深度学习中的正则化3（半监督,多任务,提前终止-解决过拟合,参数绑定与参数共享）

稀疏表示

前文所述的权重衰减直接惩罚模型参数。 另一种策略是惩罚神经网络中的激活单元，稀疏化激活单元。 这种策略间接地对模型参数施加了复杂惩罚。

我们已经讨论过$L^1$惩罚如何诱导稀疏的参数，即许多参数为零（或接近于零）。 另一方面，表示的稀疏描述了许多元素是零（或接近零）的表示。

表示的范数惩罚正则化是通过向损失函数 $J$添加对表示的范数惩罚来实现的。 我们将这个惩罚记作$\Omega (h)$。 和以前一样，我们将正则化后的损失函数记作$\tilde{J}$：
$$J(\theta ;X,y)=J(\theta ;X,y)+\alpha \Omega (h)$$
其中$\alpha \in [0,\infty ]$ 权衡范数惩罚项的相对贡献，越大的$\alpha$对应越多的正则化。

正如对参数的$L^1$惩罚诱导参数稀疏性，对表示元素的$L^1$惩罚诱导稀疏的表示： $\Omega (h)=||h|{|}_1={\sum }_i|h_i|$。除了$L^1$惩罚诱导稀疏，其他方法还包括从表示上的Student-$t$先验导出的惩罚和KL散度惩罚。

含有隐藏单元的模型在本质上都能变得稀疏。

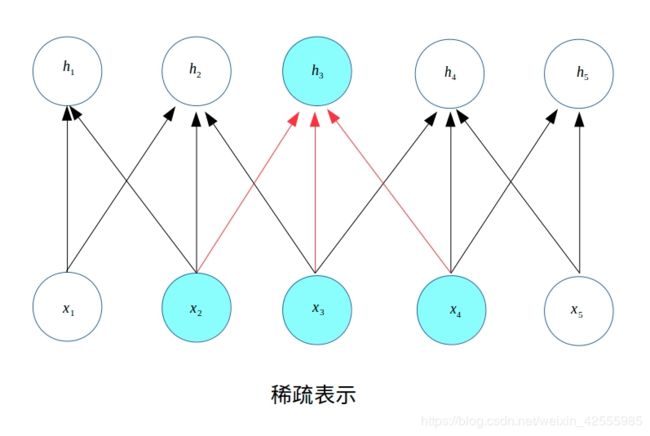
稀疏表示也是卷积神经网络经常用到的正则化方法。L¹正则化会诱导稀疏的参数，使得许多参数为0；而稀疏表示是惩罚神经网络的激活单元，稀疏化激活单元。换言之，稀疏表示是使得每个神经元的输入单元变得稀疏，很多输入是0。

例如下图，只依赖于上一层的3个神经元输入$x_1$、$x_2$、$x_3$，而其他神经元到的输入都是0。

Bagging和其他集成方法–降低泛化误差

Bagging（bootstrap aggregating）是通过结合几个模型降低泛化误差的技术。主要想法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。这是机器学习中常规策略的一个例子，被称为模型平均（model averaging）。采用这种策略的技术被称为集成方法。

Bagging是一种允许重复多次使用同一种模型、训练算法和目标函数的方法。具体来说,Bagging涉及构造k个不同的数据集。每个数据集从原始数据集中重复采样构成，和原始数据集具有相同数量的样例。

模型平均（model averaging）奏效的原因是不同的模型通常不会在测试集上产生完全相同的误差。模型平均是一个减少泛化误差的非常强大可靠的方法。例如我们假设有k个回归模型，每个模型误差是${ϵ}_i$，误差服从零均值方差为$E[{ϵ}_i^2]=v$、协方差为$E[{ϵ}_i{ϵ}_j]=c$的多维正态分布。则模型平均预测的误差为$\frac{1}{k}{\sum }_i{ϵ}_i$，均方误差的期望为$$E[(\frac{1}{k}\sum _i{ϵ}_i{)}^2]=\frac{1}{k^2}E[\sum _i({ϵ}_i^2+\sum _{j\ne i}{ϵ}_i{ϵ}_j)]=\frac{1}{k}v+\frac{k-1}{k}c$$
在误差完全相关即$c=v$的情况下，均方误差减少到$v$，所以模型平均没有任何帮助。 在错误完全不相关即$c=0$的情况下，该集成平方误差的期望仅为$\frac{1}{k}v$。 这意味着集成平方误差的期望会随着集成规模增大而线性减小。 换言之，平均上，集成至少与它的任何成员表现得一样好，并且如果成员的误差是独立的，集成将显著地比其成员表现得更好。

模型平均是一个减少泛化误差的非常强大可靠的方法。
机器学习比赛中的取胜算法通常是使用超过几十种模型平均的方法。

Dropout

Dropout可以被认为是集成大量深层神经网络的实用Bagging方法。
但是Bagging方法涉及训练多个模型，并且在每个测试样本上评估多个模型。当每个模型都是一个大型神经网络时，Bagging方法会耗费很多的时间和内存。而Dropout则提供了一种廉价的Bagging集成近似，能够训练和评估指数级数量的神经网络。

Dropout基本原理

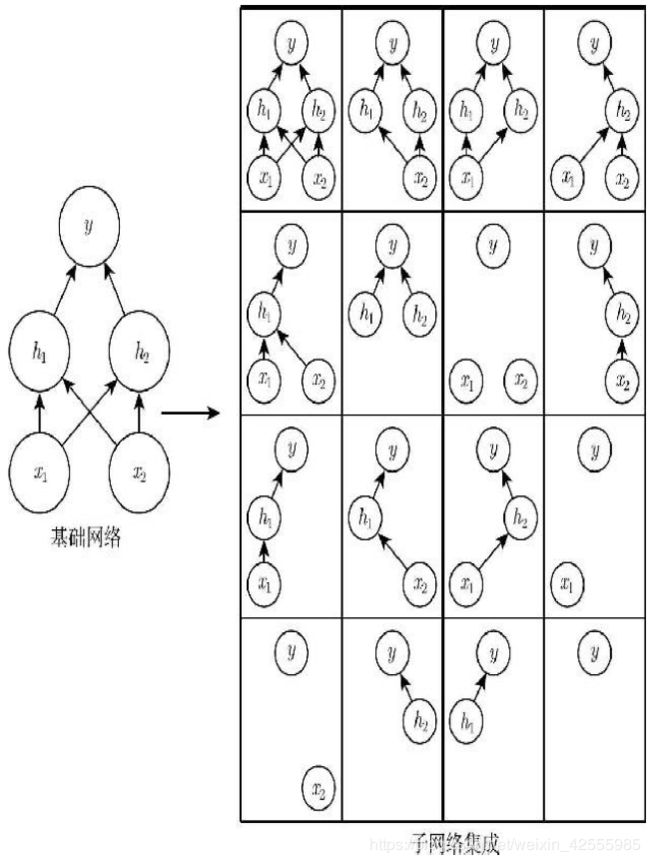
Dropout训练的集成包括所有从基础网络中除去神经元（非输出单元）后形成的子网络。只需将一些单元的输出乘零就能有效的删除一个单元（称之为乘零的简单Dropout算法）。假如基本网络有n个非输出神经元，则一共有2ⁿ个子网络。

图示说明：
Dropout训练由所有子网络组成的集成，其中子网络通过从基本网络中删除非输出单元构建。我们从具有两个可见单元和两个隐藏单元的基本网络开始。这4个单元有16个可能的子集。

右图展示了从原始网络中丢弃不同的单元子集而形成的所有16个子网络。在这个小例子中，所得到的大部分网络没有输入单元或没有从输入连接到输出的路径。当层较宽时，丢弃所有从输入到输出的可能路径的概率变小，所以这个问题不太可能在出现层较宽的网络中。

Dropout的目标是在指数级数量的神经网络上近似Bagging过程。具体来说，在训练中使用Dropout时，我们会使用基于小批量产生较小步长的学习算法，如随机梯度下降。

• 每次在小批量中加载一个样本，然后随机抽样（用于网络中所有输入和隐藏单元的）不同二值掩码。
• 对于每个单元，掩码是独立采样的。通常输入单元被包括的概率为0.8，隐藏单元被包括的概率为0.5。
• 然后与之前一样，运行前向传播、反向传播和学习更新。

Dropout与Bagging区别
A.
Bagging：所有模型都是独立的。
Dropout：所有模型共享参数，其中每个模型继承父神经网络参数的不同子集。参数共享使得在有限内存下表示指数级数量的模型变得可能。

B.
Bagging：每个模型在其相应的训练集上训练到收敛。
Dropout：大部分模型没有被显式地被训练，因为父神经网络通常很大，几乎不可能采样完指数级数量的子网络；取而代之的是，在单个步骤中训练一小部分子网络，通过参数共享使得剩余的子网络也有好的参数设定。

C.除此之外，Dropout与Bagging算法一样。例如每个子网络中遇到的训练集是有放回采样的原始训练集的一个子集。

D.模型输出
Bagging情况下，每个模型$i$产生一个概率分布$p^{(i)}(y\mid x)$，集成的预测由这些分布的算术平均值给出：$$\frac{1}{k}\sum _{i=1}^k{p}^{(i)}(y\mid x)$$
Dropout情况下，通过掩码$\mu$定义每个子模型的概率分布$p(y\mid x,\mu )$。所有掩码的算术平均值由下式给出：$$\sum _{\mu }p(\mu )p(y\mid x,\mu ),$$
其中$p(\mu )$是训练时采样$\mu$的概率分布。
但该求和包含指数级的项，一般是不可计算的，我们可以通过采样近似推断，即平均许多掩码的输出。通过几何平均直接定义的非标准化概率分布由下式给出：$$\tilde{P}\text{ensemble}(y\mid x)=\sqrt[2^d]{\prod _{\mu }p(y\mid x,\mu )}$$
其中$d$是可被丢弃的单元数。为了作出预测，需要进行标准化，例如对均匀分布的$\mu$，可按下式进行标准化：$$P_{\text{ensemble}}(y\mid x)=\frac{\tilde{P}\text{ensemble}(y\mid x)}{{\sum }_{y’}{\tilde{P}}_{\text{ensemble}}(y’\mid x)}$$

python中实现Dropout

# coding: UTF-8
'''''''''''''''''''''''''''''''''''''''''''''''''''''
   file name: dropout.py
   create time: Fri 29 Sep 2017 03:00:16 AM EDT
   author: Jipeng Huang 
   e-mail: [email protected]
   github: https://github.com/hjptriplebee
'''''''''''''''''''''''''''''''''''''''''''''''''''''
#mnist data
import tensorflow.examples.tutorials.mnist as mnist
mnist = mnist.input_data.read_data_sets("MNIST_data/", one_hot=True)

import tensorflow as tf
#ground truth
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder("float", [None,10])

#dropout
p = tf.placeholder(tf.float32)

#weight and bias
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))

#nn
h1 = tf.nn.dropout(x, keep_prob = p)
y = tf.nn.softmax(tf.matmul(h1,W) + b)

#loss and train
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(5000):
        batch_xs, batch_ys = mnist.train.next_batch(100)
        sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys, p : 0.95})
    correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
    print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels, p : 1.0}))

Dropout小结

• Dropout优点
  • 计算方便。训练过程中使用Dropout产生$n$个随机二进制数与状态相乘即可。每个样本每次更新的时间复杂度：$O(n)$，空间复杂度：$O(n)$。
  • 适用广。Dropout不怎么限制适用的模型或训练过程，几乎在所有使用分布式表示且可以用随机梯度下降训练的模型上都表现很好。包括：前馈神经网络、概率模型、受限波尔兹曼机、循环神经网络等。
  • 相比其他正则化方法（如权重衰减、过滤器约束和稀疏激活）更有效。也可与其他形式的正则化合并，得到进一步提升。
• Dropout缺点
  • 不适合宽度太窄的网络。否则大部分网络没有输入到输出的路径。
  • 不适合训练数据太小（如小于5000）的网络。训练数据太小时，Dropout没有其他方法表现好。
  • 不适合非常大的数据集。数据集大的时候正则化效果有限（大数据集本身的泛化误差就很小），使用Dropout的代价可能超过正则化的好处。
• Dropout衍生方法
  • Dropout作用于线性回归时，相当于每个输入特征具有不同权重衰减系数的L²权重衰减，系数大小由其方差决定。但对深度模型而言，二者是不等同的。
  • 快速Dropout：利用近似解的方法，减小梯度计算中的随机性析解，获得更快的收敛速度。
  • DropConnect：将一个标量权重和单个隐藏单元状态之间的每个乘积作为可以丢弃的一个单元。
  • $\mu$不取二值，而是服从正态分布，即$\mu \sim N(1,I)$