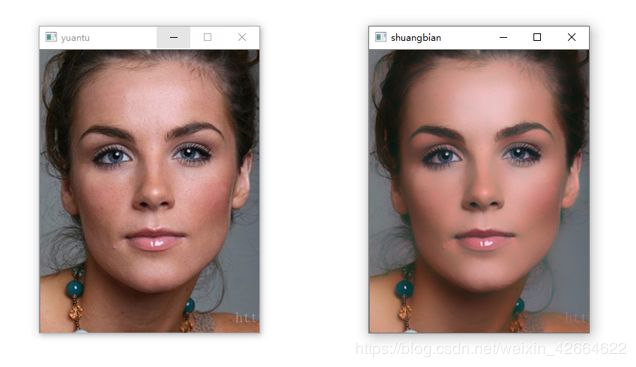
opencv + python 实现双边滤波

介绍

双边滤波是一个非线性滤波，采用的也是加权求和的方法，其权值矩阵由一个与空间距离相关的高斯函数和一个与灰度距离相关的高斯函数相乘得到。它可以达到保持边缘、降噪平滑的效果。
其权值矩阵公式为：

分析

双边滤波的权值矩阵有两部分构成，一部分是空间距离，另一部分是像素差异。
双边滤波的核函数是空间域核与像素范围域核的综合结果：在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊；在图像的边缘区域，像素值变化很大，像素范围域权重变大，从而保持了边缘的信息。

空间距离的权值矩阵计算

在有关空间距离的高斯滤波中，
对每一个元素而言，则用它周围邻域和自身的加权求和代替它自身的值，
假设滤波核是$3\times 3$，$a_5$为当前元素，
它周围8联通的像素值分别是$a_1、a_2、a_3、a_4、a_6、a_7、a_8、a_9$，
它对应的权值分别是$w_1、w_2、w_3、w_4、w_5、w_6、w_7、w_8、w_9$，
则有

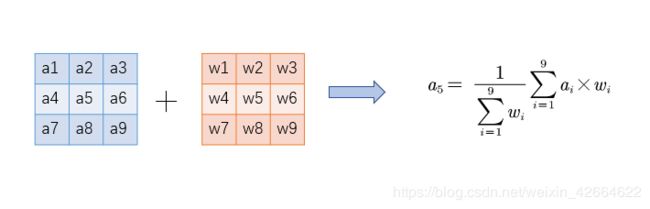
其中权值矩阵的值是由该高斯的空间距离公式决定的
$$G\text{（}x,y\text{）}=\frac{1}{\sqrt{2\Pi }{\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

1. 对于前半部分$\frac{1}{\sqrt{2\Pi }{\sigma }^2}$可以不计算，因为每一个权值都有相同的部分，那么权值归一化时就会抵消这部分。
2. 对于σ ，我们指定一个 $\sigma$ 值 ，σ 越大，那么空间高斯核函数的局部影响范围就会越大。
3. 对于 $x^2+y^2$ ，是对空间的欧拉距离的的描述，例如：$a_1$距离 $a_5$ 的横坐标差为1，纵坐标差1，则x = 1, y =1，则对应权值为$w_1=e^{-\frac{1^2+1^2}{2{\sigma }^2}}$ ，通过该方式可以计算出来每一个像素的权值。

像素差异权值矩阵计算

在像素差异的高斯滤波中，对每一个元素而言，则用它周围邻域和自身的加权求和代替它自身的值，
假设滤波核是$3\times 3$，$a_5$为当前元素，
它周围8联通的像素值分别是$a_1、a_2、a_3、a_4、a_6、a_7、a_8、a_9$，
它对应的权值分别是$w_1、w_2、w_3、w_4、w_5、w_6、w_7、w_8、w_9$，
则有

其中权值矩阵的值是由该高斯的空间距离公式决定的
$$G\text{（}x\text{）}=\frac{1}{\sqrt{2\Pi }{\sigma }^2}{e}^{-\frac{x^2}{2{\sigma }^2}}$$

1. 对于前半部分$\frac{1}{\sqrt{2\Pi }{\sigma }^2}$可以不计算，因为每一个权值都有相同的部分，那么权值归一化时就会抵消这部分。
2. 对于σ ，我们指定一个 $\sigma$ 值 ，σ 越大，那么高斯核函数的局部影响范围就会越大。
3. 对于 $x^2$ ，是对像素的差异的描述，例如：$a_1$距离 $a_5$ 的像素差为200，则x = 200 则对应权值为$w_1=e^{-\frac{200^2}{2{\sigma }^2}}$ ，通过该方式可以计算出来每一个像素的权值。对于这个矩阵，我们已知像素插值的范围一定是0-255，因此，我们可以提前计算好所有差值的权值，等到使用的时候，直接查表，提高效率。

代码

import cv2 as cv
import numpy as np
import math
import copy

def spilt( a ):
    if a/2 == 0:
        x1 = x2 = a/2
    else:
        x1 = math.floor( a/2 )
        x2 = a - x1
    return -x1,x2

def d_value():
    value = np.zeros(256)
    var_temp = 30
    for i in range(0,255):
        t = i*i
        value[i] = math.e ** (-t / (2 * var_temp * var_temp))
    return value

def gaussian_b0x(a, b):
    judge = 10
    box =[]
    x1, x2 = spilt(a)
    y1, y2 = spilt(b)
    for i in range (x1, x2 ):
        for j in range(y1, y2):
            t = i*i + j*j
            re = math.e ** (-t/(2*judge*judge))
            box.append(re)
    # for x in box :
    #     print (x)
    return box

def original (i, j, k, a, b, img):
    x1, x2 = spilt(a)
    y1, y2 = spilt(b)
    temp = np.zeros(a * b)
    count = 0
    for m in range(x1, x2):
        for n in range(y1, y2):
            if i + m < 0 or i + m > img.shape[0] - 1 or j + n < 0 or j + n > img.shape[1] - 1:
                temp[count] = img[i, j, k]
            else:
                temp[count] = img[i + m, j + n, k]
            count += 1
    return   temp

def bilateral_function(a, b, img, gauss_fun,d_value_e ):
    x1, x2 = spilt(a)
    y1, y2 = spilt(b)
    re = np.zeros(a * b)
    img0 = copy.copy(img)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            for k in range(0,2):
                temp = original(i, j, k, a, b, img0)
                # print("ave:",ave_temp)
                count = 0
                for m in  range (x1,x2):
                    for n in range(y1,y2):
                        if i+m < 0 or i+m >img.shape[0]-1 or j+n <0 or j+n >img.shape[1]-1:
                            x = img[i,j,k]
                        else :
                            x = img[i+m,j+n,k]
                        t = int(math.fabs(int(x) - int(img[i,j,k])) )
                        re[count] =  d_value_e[t]
                        count += 1
                evalue = np.multiply(re, gauss_fun)
                img[i,j,k] = int(np.average(temp, weights = evalue))
    return  img

def main():
    gauss_new = gaussian_b0x(30, 30 )
    # print(gauss_new)
    d_value_e = d_value()
    img0 = cv.imread(r"original.png")
    bilateral_img = bilateral_function(30, 30, copy.copy(img0), gauss_new, d_value_e)
    cv.imshow("shuangbian", bilateral_img)
    cv.imshow("yuantu", img0)
    cv.imwrite("shuangbian.jpg", bilateral_img)
    cv.waitKey(0)
    cv.destroyAllWindows()


if __name__  ==  "__main__":
    main()

示例

双边滤波有较好的边缘保持效果，用在人像上有美颜功效