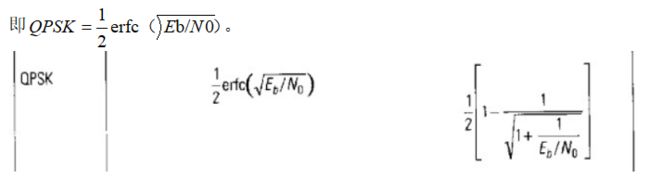MPSK通信系统的Monte Carl仿真（matlab实现，附源码）

本文旨在记录自己的一次非常用心的课程作业，以及和大家分享研究成果，喜欢的别忘了点一个赞哦~~~

实验目的

1. 提高独立学习的能力
2. 培养发现问题，解决问题，分析问题的能力
3. 学习 Matlab 的使用
4. 掌握 MPSK 通信系统的 Monte Carlo 仿真方法
5. 掌握 MPSK 通信系统的组成原理

实验内容

完成对 QPSK 通信系统的差错概率的 Monte Carlo 仿真

实验原理

1.PSK原理

PSK是利用载波的不同相位表示相应的数字信息。对于二进制相位调制（M=2)来说，两个载波相位是0和π。对于M相相位调制来说M=2k，这里k是每个传输符号的信息比特数。4PSK是M=4的载波相位调制。这里，将理论差错概率与仿真的差错概率比较，进一步观察仿真与理论值之间的差别。同时，用不同的判决准则对接受信号进行判决。并比较两种判别方法的差别。

2.调制解调原理

1．信号能量分析
一组M载波相位调制信号波形的一般表示式为
式中是发送滤波器的脉冲形状，它决定了传输信号的频谱特性，A是信号的幅度。注意到，PSK信号对所有m都具有相等的能量，即

2．噪声分析
传输信号的信道假设被加性噪声n(t)所污损，这样信号在接收端将产生误码。因为n(t)是功率谱为的白高斯过程的一个样本函数，所以噪声分量就是零均值高斯型的，即

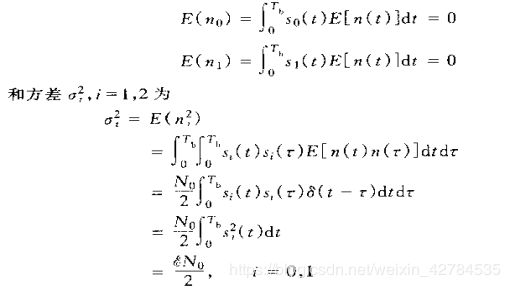
3．信号判决分析

最佳检测器将接收信号向量r投射到M个可能的传输信号向量之一上去，并选取对应于最大投影的向量。据此，得到相关准则为
检测器观察到接收信号向量，并计算r在4种可能的信号向量上的投影。根据选取对应于最大投影的信号点作为判决，从而判决出信号。同时，检测器的判决准则也可采用最小距离法，即利用星座图上符号间的距离进行判决，从而得到判决结果。

3.Monte Carlo 仿真过程

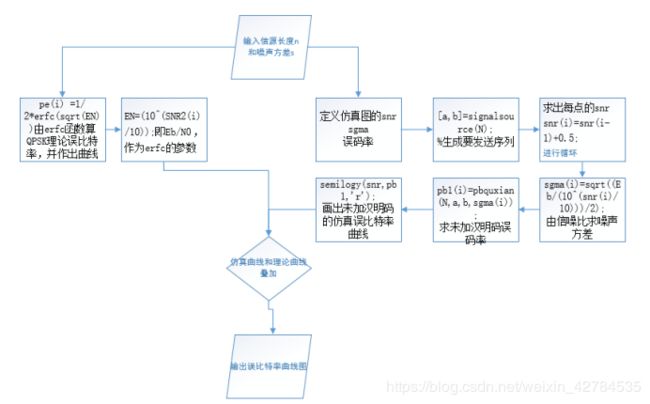
仿真框图如图1
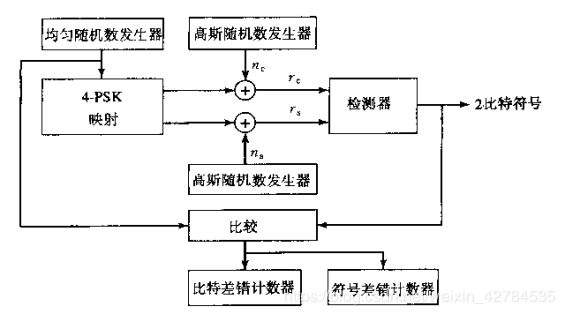图1 用于 Monte Carlo仿真的4PSK系统的方框图

如图所示，利用一个随机数发生器，产生（0，1）范围内的随机数。再将这个范围分成四个相等的区间（0，0.25），（0.25，0.5），（0.5，0.75），（0.75，1.0），这些子区间分别对应于00，01，11，10信息比特对，再用这些比特对来选择信号相位向量。加性噪声的同相分量和正交分量 ，在上面讨论过，即为零均值，方差为 的统计独立的高斯随机变量。在检测器观察到的接收信号向量 ，利用上面讨论的两种检测方法，得到判决结果，并与传输符号作比较，最后对符号差错和比特差错计数。

实验内容

（一）未加信道纠错编码的QPSK调制通信系统

子函数编写

1.二进制信源生成

函数名：function[a,b]=signalsource(N)

思路：先使用rand函数生成N个0到1之间的随机数，再生成两个一行N列的零矩阵，然后根据所在不同范围将随机数赋值给两个矩阵，得到二维数组

程序如下：

source=rand(1,N);%产生随机数
a=zeros(1,N);b=zeros(1,N);
for i=1:N
if(source(i)<0.25)%当随机数<0.25时，规定为00
    a(i)=0; b(i)=0;
elseif(source(i)<0.5)%当0.25<随机数<0.5时，规定为01    
    a(i)=0;b(i)=1;
 
elseif(source(i)<0.75)%当0.5<随机数<0.75时，规定为10

a(i)=1;
b(i)=0;else

a(i)=1;%当0.75<随机数<1时，规定为11
b(i)=1;
end
end

2.二进制信源转化为一位四进制信号

函数名：function[m]=source2(a,b,N)

思路：建立一个长度为N的序列，N的长度应为原信号长度的1/2，根据二进制序列，通过格雷映射对应为四进制序列。

程序如下：

m=zeros(1,N); 
for i=1:N
if((a(i)==0)&&(b(i)==1))%根据格雷码对照进行映射    
    m(i)=0;
elseif((a(i)==0)&&(b(i)==0))         
    m(i)=1;
elseif((a(i)==1)&&(b(i)==0))
    m(i)=2;
else m(i)=3;
end
end

3.四进制信号转换成4PSK两路正交信号

函数名：function[sm]=zhengjiaoyingshe(m,N)

思路：先生成一个二维数组，两行N列的零矩阵，从1到N循环,根据相位进行映射。当m=0时，sm=(1 0)，当m=1时，sm=(0 1)，当m=2时，sm=(-1 0)，以此类推。

程序如下：

sm=zeros(2,N);
for i=1:N
    if m(i)==0
sm(:,i)=[1;0];%当m=0时，sm=(1 0)。[1;0]中的；表示分为两行    
       elseif m(i)==1
sm(:,i)=[0;1];%当m=1时，sm=(0 1)    
       elseif m(i)==2
sm(:,i)=[-1;0];%当m=2时，sm=(-1 0)    
       elseif m(i)==3
sm(:,i)=[0;-1];%当m=3时，sm=(0 -1)    
       end
end
end

4.生成两路正交噪声

函数名：function[n]=guass(N,sgma)

思路：先生成两个零矩阵，通过rand函数产生0到1之间的随机数，计算出两路正交噪声，逐个赋值得到噪声序列。

程序如下：

nc=zeros(1,N);    
ns=zeros(1,N); 
for i=1:N
             u=rand;
             z=sgma*sqrt(2*log10(1/(1-u)));         
             u=rand;        
             gsrv1=z*cos(2*pi*u);         
             gsrv2=z*sin(2*pi*u);         
             nc(i)=gsrv1;        
             ns(i)=gsrv2; 
end

n=zeros(2,N);   %写成矩阵模式便于和之前求得的sm相加 
n(1,:)=nc; %(1,:)表示第一行的元素
n(2,:)=ns; 

end

5.最大投影准则

函数名：function[c]=touyingzhunze(r,N)

思路：将信道输出的r和原信号s逐个作向量积，通过for循环逐个比较求出最大向量积。根据映射的逆过程进行判决，恢复原信号。

程序如下：

d=zeros(1,4);
c=zeros(1,N);
for i=1:N%
d(1)=1*r(1,i)+0*r(2,i);
d(2)=0*r(1,i)+1*r(2,i);
d(3)=(-1)*r(1,i)+0*r(2,i);
d(4)=0*r(1,i)+(-1)*r(2,i);
dm=d(1);
for  k=2:4
    if dm<d(k)  dm=d(k);
if dm==d(1);
    c(i)=0;
elseif dm==d(2);c(i)=1;

elseif dm==d(3);c(i)=2;

elseif dm==d(4);c(i)=3;

6.最小距离准则

函数名：function[c]=julizhunze(r,N)

思路：分别求r向量终点与（1 0）（0 1）（-1 0）（0 -1）距离。通过for循环逐个比较求出最小距离，再进行判决得到原信号。

程序如下：

d=zeros(1,4);
c=zeros(1,N);
for i=1:N%d(1)=(r(1,i)-1)^2+(r(2,i)-0)^2;
d(2)=(r(1,i)-0)^2+(r(2,i)-1)^2;
d(3)=(r(1,i)-(-1))^2+(r(2,i)-0)^2;
d(4)=(r(1,i)-0)^2+(r(2,i)-(-1))^2;
dm=d(1);
for k=2:4%求出最小距离
    if dm>d(k)
            dm=d(k);
if dm==d(1);c(i)=0;%判决
else if dm==d(2);c(i)=1;
    else if dm==d(3);c(i)=2;
            else if dm==d(4);c(i)=3;

7.重新建立源信号

函数名：function[y]=rebuild(c,N)

思路：先生成空序列，长度为2N。对四进制信号逐个判决，当c=0，y信号为[0 1]；当c=1，y信号为[0 0]；当c=2，y信号为[1 0]；当c=3，y信号为[1 1]。

程序如下：

M=2*N;
y=zeros(1,M);%for i=1:N
    if c(i)==0
    y(2*i-1)=0;y(2*i)=1;  elseif c(i)==1
    y(2*i-1)=0;y(2*i)=0;   elseif c(i)==2
    y(2*i-1)=1;y(2*i)=0;   elseif c(i)==3
    y(2*i-1)=1;y(2*i)=1;

8.计算误比特率和误码率

函数名：function[ps,pb]=error1(y,a,b,N)

思路：统计错误比特个数和错误符号个数，初始化为0。得到的信号逐个原信号对比，如果两比特的信号中有一个比特错误则记为一个错误符号，每有一个错误比特则记为一个误比特。最后将错误比特数除以比特总数得到误比特率，将错误符号数除以符号总数得到误码率

程序如下：

numbit=0;numsymbol=0;
for i=1:N  symbol=0;
if (y(2*i-1)~=a(i))     numbit=numbit+1;    
     symbol=1;
if(y(2*i)~=b(i))
    numbit=numbit+1;
    symbol=1;
if(symbol==1)     numsymbol=numsymbol+1;
ps=numsymbol/N; pb=numbit/(2*N);

9.误比特率曲线

函数名：function[pb]=pbquxian(N,a,b,sgma)

思路：先产生四进制信号，在进行正交分为两路，再产生噪声与其相加得到r，使用判决准则恢复原先信号，最后计算误比特率。

程序如下：

m=source2(a,b,N);
sm=zhengjiaoyingshe(m,N);
n=guass(N,sgma); r=sm+n; 
c=touyingzhunze(r,N);   %c=julizhunze(r,N);  
y=rebuild(c,N);  [ps,pb]=error1(y,a,b,N);
end

最大投影点判决

A画出噪声方差分别为0、0.1、0.5、1.0时，检测器输入端输入1000个接收到的信号加噪声的样本的星座图

程序如下：

N=input('N=');%输入信源长度
s=input('方差=');%输入噪声方差
sgma=sqrt(s);%计算标准差
[a,b]=signalsource(N);%信源信号
m=source2(a,b,N);%转换成四进制
sm=zhengjiaoyingshe(m,N);%将四进制信号映射成4PSK两路正交信号 
n=guass(N,sgma);%产生噪声
r=sm+n;%加入噪声
c=touyingzhunze(r,N);%利用最小欧氏距离判决，%若用最小欧氏距离法则，则改为
%c=julizhunze(r,N);
y=rebuild(c,N);%还原信号
[ps,pb]=error1(y,a,b,N)
sprintf('符号差错概率：%2.2f%%',ps*100)
sprintf('比特差错概率：%2.2f%%',pb*100)
figure(1);
for i=1:N
if (c(i)==0)
        plot(r(1,i),r(2,i),'B*');         hold on;    
    elseif (c(i)==1)
        plot(r(1,i),r(2,i),'R*');         hold on;            
    elseif (c(i)==2)
        plot(r(1,i),r(2,i),'Y*');          hold on;              elseif (c(i)==3)        plot(r(1,i),r(2,i),'G*');           hold on;

axis([-2 2 -2 2]);
line([2,-2],[0,0],'linewidth',2,'color','red')
line([0,0],[2,-2],'linewidth',2,'color','red')
title('星座图');
hold off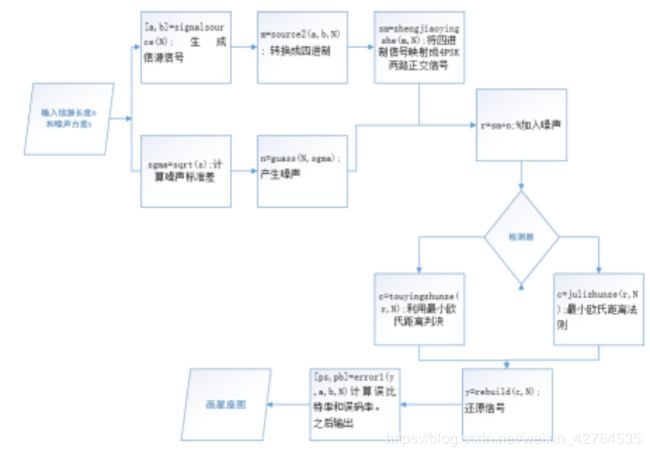

图2 QPSK最大投影判决流程图


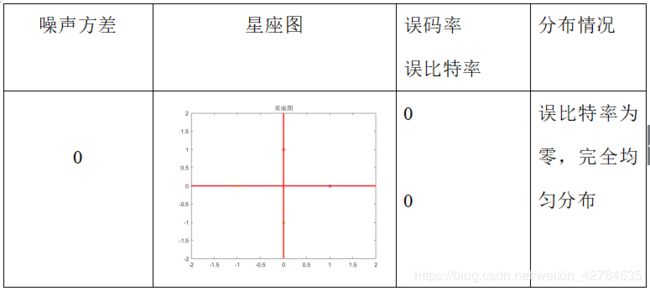
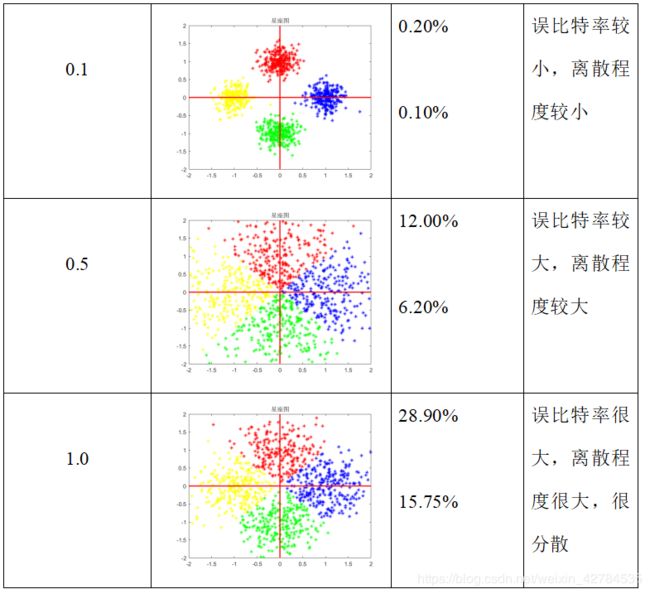
表1 QPSK最大投影判决星座图

总结：随着噪声方差的增大，误码率和误比特率不断增加，所得信号的离散程度也增加，说明噪声对原信号的影响增加

B画出数据点为1000,10000,100000时的Monte Carlo仿真误比特率曲线和理论误比特率曲线，比较差别，分析数据点的数量对仿真结果的影响（横坐标是（snr=Eb/No，格雷映射）

N=input('N=');%输入信源长度
SNR2=0:0.5:10;%理论图的信噪比范围 
Eb=1; 
snr=zeros(1,21);     %产生空序列用来定义仿真图的snr 
sgma=zeros(1,21);    %产生空序列用来定义仿真图的sgma 
pb1=zeros(1,21);    %产生空序列用来定义仿真图的未加汉明码的误码率 
snr(1)=0;    
for i=2:21    %求出每点的snr
         snr(i)=snr(i-1)+0.5; 
end
for i=1:21    %21个点循环21次，求不同i代表的信噪比对应的误码率         
      [a,b]=signalsource(N);   %生成要发送序列      
      h=xulie(a,b,N); %生成一路序列       
      sgma(i)=sqrt((Eb/(10^(snr(i)/10)))/2);   %由信噪比求噪声方差       
      pb1(i)=pbquxian(N,a,b,sgma(i));   %求未加汉明码误码率  
end
figure(2);  
semilogy(snr,pb1,'r'); %画出未加汉明码的仿真误比特率曲线 ，仿真为红色
hold on; 
for i=1:length(SNR2),%计算信噪比区间大小
    EN=(10^(SNR2(i)/10));%即Eb/N0
    pe(i) =1/2*erfc(sqrt(EN)); %QPSK理论误比特率，蓝色为理论上的误比特率    %erfc是单调增函数，在通信原理中常用于计算误码率与信噪比的关系，信噪比越高，误码率越低。
end
semilogy (SNR2,pe); 
grid 
xlabel('信噪比SNR/dB')
ylabel('误比特率') 
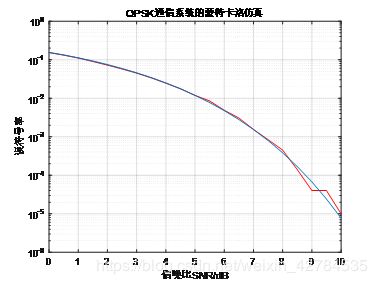
title('QPSK通信系统的蒙特卡洛仿真') 
hold off; 

图3 QPSK Monte Carlo误比特率曲线流程图

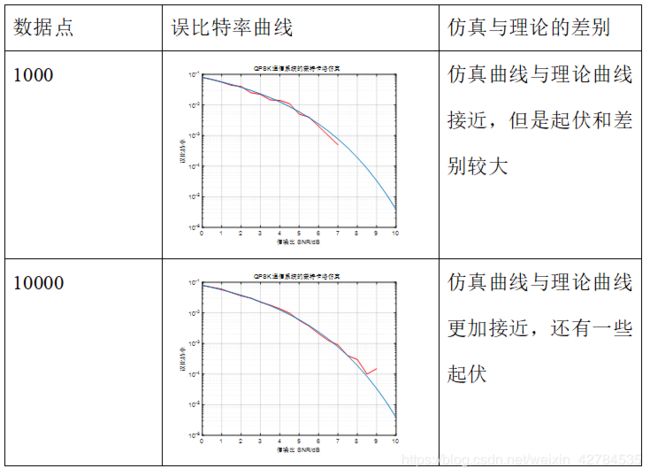
表2 QPSK Monte Carlo误比特率曲线
总结：随着数据点增加，仿真曲线和理论曲线越来越吻合。 随着信噪比增加，误比特率不断下降。

最小距离准则

图6 最小距离准则（左）和最大投影准则（右）的比较

区别：区别不大

（二）未加信道纠错编码的8PSK调制通信系统

检测器的判决准则选为最小距离法（星座图上符号间的距离），Gray格雷编码，比较数据点为100000时8PSK与QPSK的Monte Carlo仿真误比特率（或误符号率）曲线、理论误比特率（或误符号率）曲线，比较差别。

子程序编码（由于与前面相似，故不详细描述）

1.二进制信源生成

function[a,b,c]=signalsource2(N)
source=rand(1,N);%产生随机数
a=zeros(1,N);b=zeros(1,N);c=zeros(1,N);
for i=1:N
if(source(i)<0.125)%当随机数<0.25时，规定为00
a(i)=0; b(i)=0;c(i)=0;
elseif(source(i)<0.25)%当0.25<随机数<0.5时，规定为01 
a(i)=0;b(i)=0;c(i)=1;
...

2. 合并为一维序列

function[h]=xulie(a,b,c,N)
h=zeros(1,3*N);
for i=1:N
    h(3*i-2)=a(i); h(3*i-1)=b(i); h(3*i)=c(i);

3.误比特率曲线

function[pb]=pbquxian(N,a,b,c,sgma)
m=source22(a,b,c,N);
sm=yingshe(m,N);
n=guass(N,sgma);%产生两路正交高斯白噪声
r=sm+n;%将噪声与正交信号相加
d=julizhunze2(r,N);
y=rebuild(d,N);%重新还原信号
[ps,pb]=error1(y,a,b,c,N);
end

4.二进制信源转化为一位四进制信号

function[m]=source22(a,b,c,N) %将生成的原信号转换成四进制信号
m=zeros(1,N);%建立一个长度为N的序列，N的长度应为原信号长度的1/2
for i=1:N
if((a(i)==0)&&(b(i)==0)&&(c(i)==1))%根据格雷码对照进行映射    
     m(i)=0;
elseif((a(i)==0)&&(b(i)==0)&&(c(i)==1))    
     m(i)=1;
elseif((a(i)==0)&&(b(i)==1)&&(c(i)==1))            
     m(i)=2;
...

5.将四进制信号转换成4PSK两路正交信号

function[sm]=yingshe(m,N)%将四进制信号转换成4PSK两路正交信号 
sm=zeros(2,N);%生成一个二维数组
for i=1:N%从1到N循环,根据相位进行映射
    if m(i)==0
sm(:,i)=[1;0];%当m=0时，sm=(1 0)
    elseif m(i)==1
...

6.产生两路正交噪声

function[n]=guass(N,sgma) %
nc=zeros(1,N);    
ns=zeros(1,N); 
for i=1:N       
      u=rand; %产生随机数         
      z=sgma*sqrt(2*log10(1/(1-u)));         
      u=rand;        
      gsrv1=z*cos(2*pi*u);         
      gsrv2=z*sin(2*pi*u);         
      nc(i)=gsrv1;        
      ns(i)=gsrv2; 
end
n=zeros(2,N);   %写成矩阵模式便于和之前求得的sm相加 
n(1,:)=nc; 
n(2,:)=ns; 
end

7.最小距离准则

function[e]=julizhunze2(r,N)
d=zeros(1,8);
e=zeros(1,N);
for i=1:N%分别求r向量终点与（1 0）（0 1）（-1 0）（0 -1）距离
d(1)=(r(1,i)-1)^2+(r(2,i)-0)^2;
d(2)=(r(1,i)-sqrt(2)/2)^2+(r(2,i)-sqrt(2)/2)^2;
d(3)=(r(1,i)-0)^2+(r(2,i)-1)^2;
d(4)=(r(1,i)-(-sqrt(2)/2))^2+(r(2,i)-sqrt(2)/2)^2;
d(5)=(r(1,i)-(-1))^2+(r(2,i)-0)^2;
d(6)=(r(1,i)-(-sqrt(2)/2))^2+(r(2,i)-(-sqrt(2)/2))^2;
d(7)=(r(1,i)-0)^2+(r(2,i)-(-1))^2;
d(8)=(r(1,i)-sqrt(2)/2)^2+(r(2,i)-(-sqrt(2)/2))^2;
dm=d(1);
for k=2:8%求出最小距离
    if dm>d(k)
            dm=d(k);
if dm==d(1);e(i)=0;%判决
else if dm==d(2);e(i)=1;   else if dm==d(3);e(i)=2;    else if dm==d(4);e(i)=3;   else if dm==d(5);e(i)=5;   
else if dm==d(6);e(i)=6;     else if dm==d(7);e(i)=7;    else if dm==d(8);e(i)=8;

8.恢复原信号

function[y]=rebuild(d,N)%重新建立源信号
M=3*N;
y=zeros(1,M);%生成空序列，长度为3N
for i=1:N
    if d(i)==0
y(3*i-2)=0;y(3*i-1)=0;y(3*i)=0;%当c=0，y信号为[0 0 0]
    elseif d(i)==1y(3*i-2)=0;
y(3*i-1)=0;y(3*i)=1;%当c=1，y信号为[0 0 1]
    elseif d(i)==2
    ...

9.计算误比特率和误码率

function[ps,pb]=error1(y,a,b,c,N)
numbit=0;%统计错误比特个数，初始化为0
numsymbol=0;%统计错误符号个数，初始化为0
for i=1:N    symbol=0;
if (y(3*i-2)~=a(i))%统计错误比特个数    numbit=numbit+1;   symbol=1;
if(y(3*i-1)~=b(i))    numbit=numbit+1;  symbol=1;
if(y(3*i)~=c(i))    numbit=numbit+1;  symbol=1;
if(symbol==1)%统计错误符号个数    
    numsymbol=numsymbol+1;ps=numsymbol/N;%计算错误率pb=numbit/(3*N);

最小距离准则

N=input('N=');%输入信源长度
SNR2=0:0.5:10;%理论图的信噪比范围 
Eb=1; 
snr=zeros(1,21);     %产生空序列用来定义仿真图的snr 
sgma=zeros(1,21);    %产生空序列用来定义仿真图的sgma 
pb1=zeros(1,21);    %产生空序列用来定义仿真图的未加汉明码的误码率 
snr(1)=0;    
for i=2:21    %求出每点的snr     
    snr(i)=snr(i-1)+0.5; 
end
for i=1:21    %21个点循环21次         
    [a,b,c]=signalsource2(N);   %生成要发送序列      
    h=xulie(a,b,c,N);        
    sgma(i)=sqrt((Eb/(10^(snr(i)/10)))/2);   %由信噪比求噪声方差       
    pb1(i)=pbquxian(N,a,b,c,sgma(i));   %求未加汉明码误码率 
end
figure(2);  
semilogy(snr,pb1,'r'); %画出未加汉明码的仿真误比特率曲线 
hold on; 
for i=1:length(SNR2),%计算信噪比区间大小     
N0=Eb/(10^(SNR2(i)/10));    
pe(i)=2*qfunc(sqrt(2/N0)*sin(pi/8));
end
semilogy (SNR2,pe); 
grid 
xlabel('信噪比/dB')
ylabel('误比特率') 
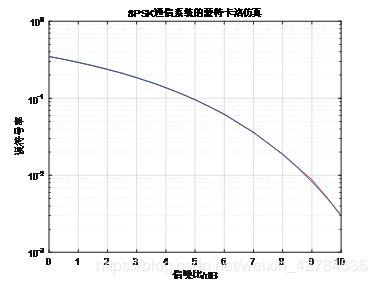
title('8PSK通信系统的蒙特卡洛仿真') 
hold off; 

图4 8PSK和QPSK的误符号率曲线

总结：二者在低SNR时区别不大，但是高SNR时，QPSK可以达到非常低的误码率，而8PSK则不行，所以在高SNR时QPSK优于8PSK。

总结

1.问题

1）刚开始进行高斯噪声输出时，使用的是第一种方法，但是仿真曲线和理论曲线差别很大，后来改为n=normrnd(0,sgma,[2,N]);后二者吻合。

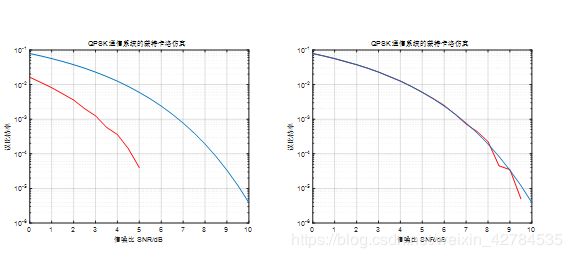
图5 第一种方法结果（左）第一种方法结果（右）

2）求QPSK理论的误比特率曲线时，刚开始函数错误，后来在网上查阅得知使用erfc函数直接可以使用，改正为此。

3）进行最小距离判决的时候，输出仿真曲线误比特率一直在75%左右，后来检查代码才发现是最小距离判决的子函数中，在函数内部提前写了end语句，导致函数提前结束，造成较高误比特率。

2.对于理论的理解

格雷码是一种绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码，是一种错误最小化的编码方式，因为，虽然自然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况，例如从十进制的3转换为4时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻位间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同，引起数字量发生变化时，格雷码仅改变一位，这样与其它编码同时改变两位或多位的情况相比更为可靠，即可减少出错的可能性。

格雷码是一个数列集合，相邻两数间只有一个位元改变，为无权数码，且格雷码的顺序不是唯一 的。

格雷码的构造方法为： 直接排列以二进制为0值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反覆，即可排列出n个位元的格雷码。

3.感悟

1、 这次实验工作量比较大，而且很多matlab函数不熟悉，经过各种查资料、请教同学，才最终完成。遇到的最大困难是编程有错误还老是查不出来，以后要多熟悉熟悉matlab函数，减少在编程上的困难。这次实验收获良多，学会了不少东西，相信下次实验会轻松不少。
2、这次实验开始总是仿真不到需要的图形，理论和仿真差距很大。后来通过交流，修改了程序，改变一些变量，才最终仿真出一些比较满意的结果。
3、最大的收获是一定要冷静，保持平常心，尤其是在调试程序时，要稳重，忌焦忌燥，否则会越来越麻烦。

都看到这里了不如点个赞哦~