博弈论与人工智能
博弈论与人工智能
概要
本文主要阐述:
- 什么是博弈论?
- 博弈论如何应用于人工智能
介绍
《美丽心灵》这部经典影片,相信很多人都看过。这部影片的主人公就是诺贝尔经济学奖获得者 John Nash.
在影片的一个经典场景中,Nash说到 “….the best outcome would come when everyone in the group is doing what’s best for himself and the group.” 很多人把这个认为是对著名的纳什均衡的描述,其实这句话刻画的是帕累托最优。但是这并不影响我们对博弈论的一个初步感观。
本文主要介绍基本的博弈论知识和概念,并且深入探讨博弈论如何应用到人工智能领域。
什么是博弈论
我相信大部分的人都曾经接触过甚至使用过博弈论的相关概念和方法,但是却没有真正的深入研究。
首先,给出博弈论的正式定义:
“Game Theory can be referred to as the modeling of the possible interactions between two or more Rational Agents or players. ”
这里,Rational(明智,理智)这个词非常重要,它可以说是博弈论的基础。
我们可以简单理解为:Rational指的是参与博弈的每一个人都知道其他参与者都与他同样理智且掌握同样的知识、理解整个游戏,同时都追求利益最大化且了解他人也是如此。简单来说就是每个人都是利己的且追求利益最大化的。
现在我们需要明确一下博弈论中的其他相关概念:
- Game(游戏): 在泛化的场景中,游戏包含了一些参与者、行为和策略以及最终收益。例如拍卖、棋类、政治等。
- Players(参与者):是指参与到游戏中的具有理智的实体。例如拍卖会上的竞价者、玩剪刀-石头-布的玩家、参加竞选的政客。
- Payoff(收益):收益也可以称为奖励,是玩家在参与游戏中会得到的一个结果,可以为正也可以为负。
纳什均衡
纳什均衡可以认为是博弈论实现人工智能的一个基本基石。它是每一个参与者所选择的一种行为,可使没有参与者会改变这种行为,因为改变会使其不是最优选择;或者说在考虑其他参与者是理智的,也会选择他们的最优策略的情况下,纳什均衡是某参与者的最佳选择。
在参与者的可选行为集下,他不可能通过改变策略而提高其收益了,我们可以认为纳什均衡的选择是无悔的。
让我们来考虑一个博弈论中最经典的例子:囚徒困境(The Prisoner’s Dilemma )。这个例子解释了在存在共同或互斥利益、共同合作行为的场景下,参与者是如何考虑其个人利益的。
假设有两个同案犯,Alan和Ben,他们被分开审问,那么有两个选择:保持沉默和认罪。考虑他们两个人的选择的组合有四种:
- {沉默,沉默}
- {认罪,沉默}
- {沉默,认罪}
- {认罪,认罪}
以收益矩阵表示:
上图中的A代表Alan的收益,B代表Ben的收益,负数代表是负收益:
- 如果两个人都保持沉默,那么每个人都会被判1年监禁。
- 如果有一个认罪的,将会被转为污点证人而被释放,而另外一个人将会判15年监禁。
- 如果两个人都认罪,则每个人会判10年监禁。
在这种情况下,该如何选择呢?这个困境主要是因为他们都不知道对方的选择会是什么,对于他们来说最优选择显然是上图中的左上角,也就是都保持沉默,这是集体利益是最大化的。
但是这个游戏的纳什均衡是什么呢?显然不是这个集体最优策略,因为任何一个人都可以通过改变策略,就是从沉默变成认罪,而是自己得到利益最大化。所以,让我们仔细分析和思考一下:
Alan会做如下推理:假如Ben沉默,我当然是认罪更好一些,因为我会无罪释放的;假如Ben认罪,我也是认罪最后,所以我还是认罪吧。同理,Ben也会做类似的推理,所以这个游戏的纳什均衡是两个人都认罪,也就是图中右下角的结果。
博弈的类型
类似囚徒困境这种两个人同时做出决策,可以表示为一个博弈矩阵,这种类型的博弈通常称为规范形式博弈(Normal form game)。在博弈论中,根据不同的原则,博弈可以被分为不同的类别。
代理之间的交互
直观来说,我们可以根据博弈中的参与者是寻求合作还是竞争来对博弈进行分类。政治运动是竞争性博弈的一个例子;而篮球队内博弈则是合作性博弈。
代理如何参与
我们也可以根据代理者是同时的还是延展的来对博弈进行分类。让我们来举个例子,一个称为"性别大战"的经典博弈:
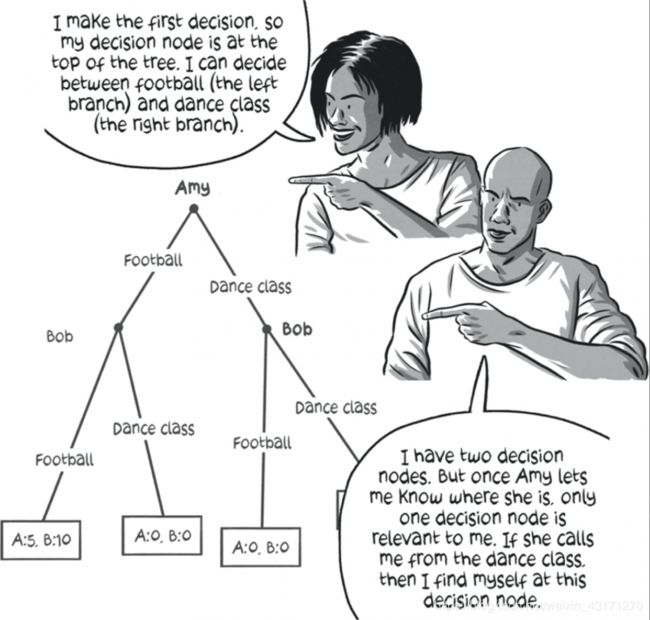
考虑Bob和Amy认识很久,且彼此喜欢对方,他们也都知道对方的习惯和爱好。Bob喜欢看足球而Amy喜欢跳舞。他们也都想顺从对方,这样他们就可以给对方一个惊喜或者见面聊天。
如果他们希望给对方惊喜,同时他们不知道对方周末的计划是什么,那么就可能产生如下的博弈矩阵:
这个博弈矩阵说明如果他们互相错过了,他们没有任何收益。这展示了在预先不知道对方的计划的时候同时做出决策的情况。
另外,如果他们彼此合作且告诉对方自己的行动计划是什么,那么该博弈将演化成如下形式:
这种情况被称为扩展形式或者回合制博弈,每一个参与者可以看到另外一个参与者的行为。石头-剪刀-布就是一个同时性的博弈;Tic-Tac-Toe是一个扩展性的博弈。
基于信息
在博弈论中,当参与者所了解的是不完全的信息时,情况会有所变化。他们可能不了解其他参与者所有可能的策略或者潜在的收益。参与者可能也不清楚他们所要对付的是什么人和其动机是什么。
基于信息的了解程度,博弈可分为
-
完美信息博弈
Tic-Tac-Toe是一个典型的完美信息博弈,每一个参与者都掌握如下知识
- 所有其他参与者的可能行为
- 他们正在采取什么行动
- 他们所得到的收益是什么
-
不完美信息博弈
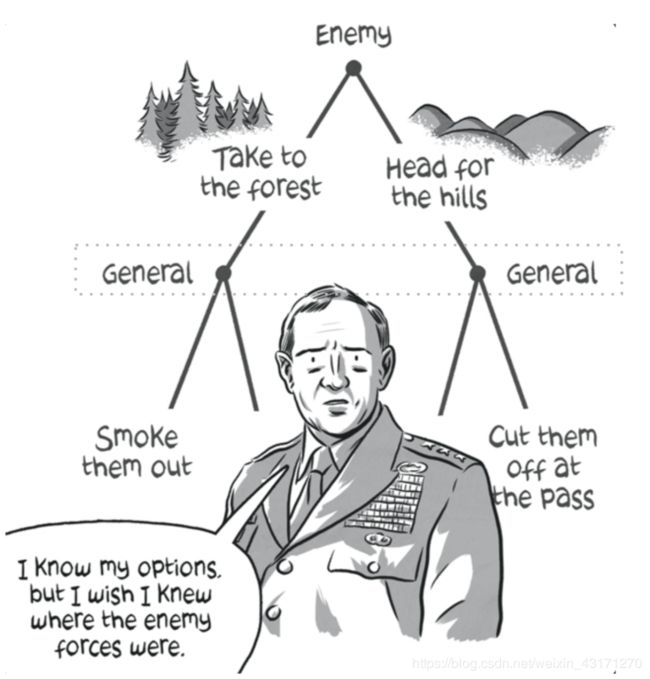
在这种情况下,参与者了解其他参与者的属性和动机,以及他们在各种情况下的收益,但是不清楚他们正在采取什么行动。
上图中,将军知道敌人的动机和在各种场景下的收益,但是他不知道敌人隐藏在什么地方。因此,将军不知道他所在的决策点的位置。不完美信息博弈在真实场景中是经常出现的。
-
不完整信息博弈
不完全信息博弈是非常适合对真实世界进行建模的。在这种情况下,参与者甚至不知道其他参与者的类型是什么。即使参与者可以看到其他参与者所采取的行动,他并不清楚其他参与者的动机和采取某种行为所产生的收益。不完全信息博弈是最广泛的博弈形式。扑克游戏是非常典型的不完全信息游戏。
人工智能与博弈论
读者可能会疑惑,前面所说的这些东西和人工智能又有什么关系呢?下面我们来探讨这个问题。
博弈论在人工智能领域可以用来辅助决策。事实上博弈论已经用在人工智能领域,那就是GAN Generative Adversarial Network,生成对抗网络。人工智能和深度学习领域的先驱者Yann LeCun认为GAN是 "The coolest idea in machine learning in the last twenty years. "。
那么博弈论又是如何帮助GAN的呢?要回答这个问题,我们首先需要了解一下GAN的一些基础知识:
一个GAN网络是由两个神经网络组成的,名为:
-
Generator (生成器)
-
Discriminator(判别器)
生成器是一个神经网络,随机产生图像;判别器尝试来判断所给的图像是生成出来的假的图像还是来自训练数据集。如果图像被判定为是生成的或者是假的,生成器会调整其参数;相反如果识别错误,判别器会调整其参数。
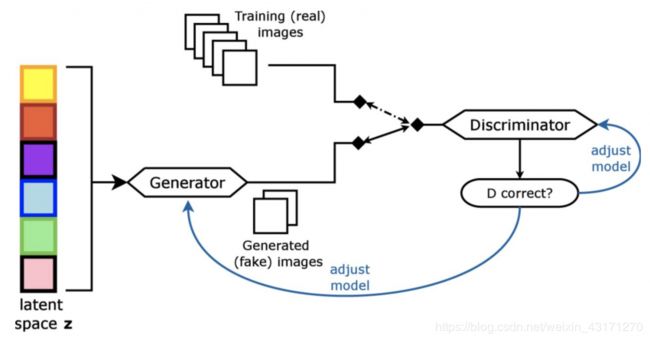
这个竞争过程会持续直到一个没有可改善的空间的状态,而这个状态就是纳什均衡。这是一个在两个神经网络之间的博弈,在整个过程中,每个神经网络都在不断优化自身,最后达到纳什均衡。 博弈论的最核心的实践是在不完美信息博弈。而扑克游戏的AI应用经常会作为解决不完美信息博弈问题的一个基准。在真实世界中,不完美信息博弈非常重要。在人工智能的发展史上,机器学习和深度学习在解决不完美信息博弈问题的表现还不够成功。
德州扑克就是不完美信息博弈的一个例子,因为对手手中的牌你是看不到的。这是一个非常有挑战的问题,其可能的状态大概有10的161次方之多。(目前,宇宙中可观察道德原子总数为10的82次方)。有不少人曾尝试使用深度学习和深度强化学习来解决这个问题,但是效果差强人意。
但是一个名为Libratus的AI程序的表现超过了任何其他方法,它在20000人的大赛中赢得了冠军。该程序是由卡内基梅隆大学开发,并没有采用任何机器学习和深度学习方法。它的设计核心理念就是博弈论。
人们经常会因为机器学习和深度学习针对真实世界场景所带来的一些副作用而争辩。因为真实世界的问题往往属于不完美信息博弈问题,而机器学习和深度学习常常受阻于此类问题。博弈论是逐渐地推动增益的一种方案,它在真实世界案例中有很强的泛化能力。
总结
本文我们讨论了博弈论的一些核心概念和与人工智能的结合,也介绍了现实中的实践成果。当然这个问题还远远没有解释完整。有很多人在人工智能的很多方面都采用了博弈论的理念,例如 “AI for Social Good" 针对公共安全、野生环境保护和公众健康的AI解决方案的研究,又例如模型解释领域中的Shap Value(可参见本人机器学习讲义-模型解释)等。就这个话题,欢迎大家和我讨论。