机器学习笔记(九)——数据降维:主成分分析法(PCA)
一、主成分分析法(PCA)思想及原理
(一) 什么是主成分分析法
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法(非监督的机器学习方法)。
其最主要的用途在于“降维”,通过析取主成分显出的最大的个别差异,发现更便于人类理解的特征。也可以用来削减回归分析和聚类分析中变量的数目。
(二)为什么要做主成分分析
在很多场景中需要对多变量数据进行观测,在一定程度上增加了数据采集的工作量。更重要的是:多变量之间可能存在相关性,从而增加了问题分析的复杂性。
如果对每个指标进行单独分析,其分析结果往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。
(三)
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
先假设用数据的两个特征画出散点图:

如果我们只保留特征1或者只保留特征2。那么此时就有一个问题,留个哪个特征比较好呢?
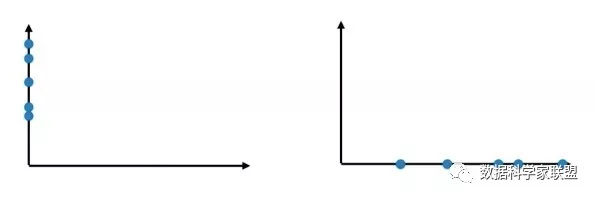
通过上面对两个特征的映射结果可以发现保留特征1(右面)比较好,因为保留特征1,当把所有的点映射到x轴上以后,点和点之间的距离相对较大,也就是说,拥有更高的可区分度,同时还保留着部分映射之前的空间信息。
那么如果把点都映射到y轴上,发现点与点距离更近了,这不符合数据原来的空间分布。所以保留特征1相比保留特征2更加合适,但是这是最好的方案吗?
将所有的点都映射到一根拟合的斜线上,从二维降到一维,整体和原样本的分布并没有多大的差距,点和点之间的距离更大了,区分度也更加明显。
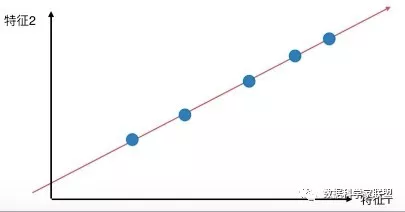
也就是说,我们要考虑的问题是:
如何找到让样本间距最大的轴?
其中,一般我们会使用方差(Variance)来定义样本之间的间距:
V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 Var(x)=\frac {1}{m}\sum_{i=1}^m(x_i-\bar x)^2 Var(x)=m1i=1∑m(xi−xˉ)2
(四)主成分分析法的步骤
对于如何找到一个轴,使得样本空间的所有点映射到这个轴的方差最大。
- 第一步:样本归0
将样本进行均值归0(demean),即所有样本减去样本的均值。样本的分布没有改变,只是将坐标轴进行了移动。
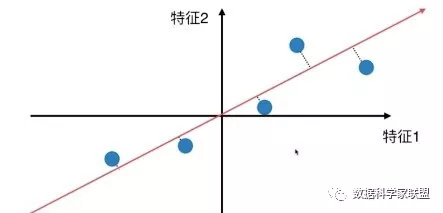
此时对于方差公式: V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 , x ˉ = 0 Var(x)=\frac {1}{m}\sum_{i=1}^m(x_i-\bar x)^2,\bar x=0 Var(x)=m1∑i=1m(xi−xˉ)2,xˉ=0。其中此时计算过程就少一项,这就是为什么要进行样本均值归0,可以化简的更加方便。
- 第二步:找到样本点映射后方差最大的单位向量ω
求一个轴的方向w=(w1,w2)需要定义一个轴的方向w=(w1, w2),使得我们的样本,映射到w以后,使得X映射到w之后的方差最大:
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X p r o j e c t i − x ˉ p r o j e c t ) 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m(X_{project}^i-\bar x_{project})^2 Var(Xproject)=m1i=1∑m(Xprojecti−xˉproject)2
其实括号中的部分是一个向量,更加准确的描述应该是(向量的模):
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ∣ ∣ X p r o j e c t i − x ˉ p r o j e c t ∣ ∣ 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m||X_{project}^i-\bar x_{project}||^2 Var(Xproject)=m1i=1∑m∣∣Xprojecti−xˉproject∣∣2
因为前面已经去均值,所以,这里只需下面的式子最大:
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ∣ ∣ X p r o j e c t i ∣ ∣ 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m||X_{project}^i||^2 Var(Xproject)=m1i=1∑m∣∣Xprojecti∣∣2
映射过程如下:
红色的线是我们要找的方向 ω = ( ω 1 , ω 2 ) ω=(ω_1,ω_2) ω=(ω1,ω2) ;第i行的样本点 X ( i ) = ( X 1 ( i ) , X 2 ( i ) ) X^{(i)}=(X_1^{(i)},X_2^{(i)}) X(i)=(X1(i),X2(i)), X ( i ) X^{(i)} X(i)此时也是一个向量;映射到ω上做一个垂线,交点的位置就是 X p r o j e c t ( i ) = ( X p r o 1 ( i ) , X p r o 2 ( i ) ) X_{project}^{(i)}=(X_{pro1}^{(i)},X_{pro2}^{(i)}) Xproject(i)=(Xpro1(i),Xpro2(i))对应的点;真正要求 X p r o j e c t ( i ) X_{project}^{(i)} Xproject(i)的的模的平方,蓝色线段长度对应的平方。
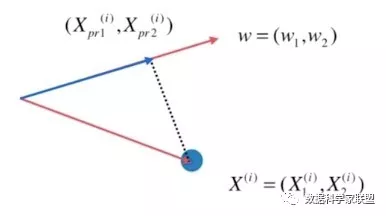
把一个向量映射到另一个向量上,对应的映射长度是多少。实际上这种映射就是点乘:
X ( i ) ⋅ ω = ∣ ∣ X ( i ) ∣ ∣ ⋅ ∣ ∣ ω ∣ ∣ ⋅ c o s θ X^{(i)}\cdot ω=||X^{(i)}||\cdot ||ω||\cdot cosθ X(i)⋅ω=∣∣X(i)∣∣⋅∣∣ω∣∣⋅cosθ
因为向量ω是我们要找的轴,是一个方向,因此使用方向向量就可以。因此长度为1:
X ( i ) ⋅ ω = ∣ ∣ X ( i ) ∣ ∣ ⋅ c o s θ X^{(i)}\cdot ω=||X^{(i)}||\cdot cosθ X(i)⋅ω=∣∣X(i)∣∣⋅cosθ
因此,在三角形中有:
X ( i ) ⋅ ω = ∣ ∣ X p r o j e c t ( i ) ∣ ∣ X^{(i)}\cdot ω=||X_{project}^{(i)}|| X(i)⋅ω=∣∣Xproject(i)∣∣
主成分分析法的目标是:
求ω,使得 V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X ( i ) ⋅ ω ) 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m(X^{(i)}\cdot ω)^2 Var(Xproject)=m1∑i=1m(X(i)⋅ω)2最大.
如果是n维数据,则有: V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X 1 ( i ) ω 1 + X 2 ( i ) ω 2 + … … + X n ( i ) ω n ) 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m(X_1^{(i)}ω_1+X_2^{(i)}ω_2+……+X_n^{(i)}ω_n)^2 Var(Xproject)=m1∑i=1m(X1(i)ω1+X2(i)ω2+……+Xn(i)ωn)2
(五)小结
主成分分析方法(PCA),是数据降维算法。将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,即用较少的综合指标分别代表存在于各个变量中的各类信息,达到数据降维的效果。
所用到的方法就是“映射”:将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。我们要选择的就是让映射后样本间距最大的轴。
其过程分为两步:
样本归0
找到样本点映射后方差最大的单位向量ω
最后就能转为求目标函数的最优化问题:
求ω,使得 V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X ( i ) ⋅ ω ) 2 Var(X_{project})=\frac {1}{m}\sum_{i=1}^m(X^{(i)}\cdot ω)^2 Var(Xproject)=m1∑i=1m(X(i)⋅ω)2最大
此时,我们就可以用搜索策略,使用梯度上升法来解决。
二、PCA算法的实现及使用
(一)PCA算法梯度求解
对于最优化问题,除了求出严格的数据解以外,还可以使用搜索策略求极值。
在求极值的问题中,有梯度上升和梯度下降两个最优化方法。梯度上升用于求最大值,梯度下降用于求最小值。
1. 梯度上升&梯度下降
梯度下降的思想及推导问题。已知:使损失函数值变小的迭代公式:
( a k + 1 , b k + 1 ) = ( a k + 1 − η ∂ L ∂ a , b k + 1 − η ∂ L ∂ b ) (a_{k+1},b_{k+1})=(a_{k+1}-η\frac {\partial L}{\partial a},b_{k+1}-η\frac {\partial L}{\partial b}) (ak+1,bk+1)=(ak+1−η∂a∂L,bk+1−η∂b∂L)
我们现在要求极大值,则使用梯度上升法。梯度的方向就是函数值在该点上升最快的方向,顺着这个梯度方向轴,就可以找到极大值。即将负号变为正号:
( a k + 1 , b k + 1 ) = ( a k + 1 + η ∂ L ∂ a , b k + 1 + η ∂ L ∂ b ) (a_{k+1},b_{k+1})=(a_{k+1}+η\frac {\partial L}{\partial a},b_{k+1}+η\frac {\partial L}{\partial b}) (ak+1,bk+1)=(ak+1+η∂a∂L,bk+1+η∂b∂L)
2.求梯度
现在回到对PCA算法求解的问题上来,对于 PAC 的目标函数:
求 ω 使 得 f ( X ) V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X 1 ( i ) ω 1 + X 2 ( i ) ω 2 + … … + X n ( i ) ω n ) 2 求ω使得f(X)Var(X_{project})=\frac {1}{m}\sum_{i=1}^m(X_1^{(i)}ω_1+X_2^{(i)}ω_2+……+X_n^{(i)}ω_n)^2 求ω使得f(X)Var(Xproject)=m1∑i=1m(X1(i)ω1+X2(i)ω2+……+Xn(i)ωn)2
最大,可以使用梯度上升法来解决。
首先要求梯度。在上式中,ω是未知数 X i X_i Xi是非监督学习提供的已知样本信息。因此对 f ( X ) f(X) f(X)中ω的每一个维度进行求导:
ᐁ f = ( ∂ f ∂ ω 1 ∂ f ∂ ω 2 … ∂ f ∂ ω n ) = 2 m ( ∑ i = 1 m ( X 1 ( i ) ω 1 + X 2 ( i ) ω 2 + … + X n ( i ) ω n ) X 1 ( i ) ∑ i = 1 m ( X 1 ( i ) ω 1 + X 2 ( i ) ω 2 + … + X n ( i ) ω n ) X 2 ( i ) … ∑ i = 1 m ( X 1 ( i ) ω 1 + X 2 ( i ) ω 2 + … + X n ( i ) ω n ) X n ( i ) ) ᐁf=\begin{pmatrix} \frac {\partial f}{\partial ω_1}\\ \frac {\partial f}{\partial ω_2}\\ …\\ \frac {\partial f}{\partial ω_n}\end{pmatrix}=\frac {2}{m}\begin{pmatrix} \sum_{i=1}^m(X_1^{(i)}ω_1+X_2^{(i)}ω_2+…+X_n^{(i)}ω_n)X_1^{(i)}\\ \sum_{i=1}^m(X_1^{(i)}ω_1+X_2^{(i)}ω_2+…+X_n^{(i)}ω_n)X_2^{(i)}\\ …\\ \sum_{i=1}^m(X_1^{(i)}ω_1+X_2^{(i)}ω_2+…+X_n^{(i)}ω_n)X_n^{(i)}\end{pmatrix} ᐁf=⎝⎜⎜⎜⎛∂ω1∂f∂ω2∂f…∂ωn∂f⎠⎟⎟⎟⎞=m2⎝⎜⎜⎜⎛∑i=1m(X1(i)ω1+X2(i)ω2+…+Xn(i)ωn)X1(i)∑i=1m(X1(i)ω1+X2(i)ω2+…+Xn(i)ωn)X2(i)…∑i=1m(X1(i)ω1+X2(i)ω2+…+Xn(i)ωn)Xn(i)⎠⎟⎟⎟⎞
对上式进行合并,写成两个向量点乘的形式。更进一步对表达式进行向量化处理
ᐁ f = 2 m ( ∑ i = 1 m ( X ( i ) ω ) X 1 ( i ) ∑ i = 1 m ( X ( i ) ω ) X 2 ( i ) … ∑ i = 1 m ( X ( i ) ω ) X n ( i ) ) ᐁf=\frac {2}{m}\begin{pmatrix} \sum_{i=1}^m(X^{(i)}ω)X_1^{(i)}\\ \sum_{i=1}^m(X^{(i)}ω)X_2^{(i)}\\ …\\ \sum_{i=1}^m(X^{(i)}ω)X_n^{(i)}\end{pmatrix} ᐁf=m2⎝⎜⎜⎜⎛∑i=1m(X(i)ω)X1(i)∑i=1m(X(i)ω)X2(i)…∑i=1m(X(i)ω)Xn(i)⎠⎟⎟⎟⎞
ᐁ f = 2 m ( X ( 1 ) ω , … , X ( m ) ω ) ⋅ ( X 1 ( 1 ) , X 2 ( 1 ) , … , X n ( 1 ) X 1 ( 2 ) , X 2 ( 2 ) , … , X n ( 2 ) … X 1 ( m ) , X 2 ( m ) , … , X n ( m ) ) ᐁf=\frac {2}{m}(X^{(1)}ω,…,X^{(m)}ω)\cdot \begin{pmatrix} X_1^{(1)},X_2^{(1)},…,X_n^{(1)}\\ X_1^{(2)},X_2^{(2)},…,X_n^{(2)}\\ …\\ X_1^{(m)},X_2^{(m)},…,X_n^{(m)}\end{pmatrix} ᐁf=m2(X(1)ω,…,X(m)ω)⋅⎝⎜⎜⎜⎛X1(1),X2(1),…,Xn(1)X1(2),X2(2),…,Xn(2)…X1(m),X2(m),…,Xn(m)⎠⎟⎟⎟⎞
ᐁ f = 2 m ⋅ ( X ω ) T ⋅ X = 2 m ⋅ X T ⋅ ( X ω ) ᐁf=\frac {2}{m}\cdot (Xω)^T\cdot X=\frac {2}{m}\cdot X^T\cdot (Xω) ᐁf=m2⋅(Xω)T⋅X=m2⋅XT⋅(Xω)
得到梯度为:
ᐁ f = 2 m ⋅ X T ⋅ ( X ω ) ᐁf=\frac {2}{m}\cdot X^T\cdot (Xω) ᐁf=m2⋅XT⋅(Xω)
有了梯度,就可以使用梯度上升法求最大值了。
(二)求解第一主成分代码实现
我们已经知道了PCA算法的目标函数(方差),以及如何使其最大(梯度上升)。下面使用代码来实现公式及算法流程。
下面我们以二维数据为例,将其映射到一维,即求出一系列样本点的第一主成分。
1 数据准备
首先准备数据:
import numpy as np
import matplotlib.pyplot as plt
X = np.empty([100,2])
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0., 10., size=100)
plt.scatter(X[:,0],X[:,1])
plt.show()
2. 函数实现
接下来对数据进行主成分分析,第一步是均值归零,定义相应的函数。
将样本进行均值归0(demean),即所有样本将去样本的均值。样本的分布没有改变,只是将坐标轴进行了移动。
其方法是:X表示一个矩阵,每一行代表一个样本,每一个样本的每一个特征都减去这个特征的均值。实现如下:
def demean(X):
# axis=0按列计算均值,即每个属性的均值,1则是计算行的均值
return (X - np.mean(X, axis=0))
X_demean = demean(X)
# 注意看数据分布没变,但是坐标已经以原点为中心了
plt.scatter(X_demean[:, 0], X_demean[:, 1])
plt.show()
首先定义目标函数:
def f(w,X):
return np.sum((X.dot(w)**2))/len(X)
然后根据梯度公式 ᐁ f = 2 m ⋅ X T ⋅ ( X ω ) ᐁf=\frac {2}{m}\cdot X^T\cdot (Xω) ᐁf=m2⋅XT⋅(Xω)求梯度:
def df_math(w,X):
return X.T.dot(X.dot(w))*2./len(X)
现在对其稍加改造,可以验证我们之前计算的梯度表达式的结果是否正确。
# 验证梯度求解是否正确,使用梯度调试方法:
def df_debug(w, X, epsilon=0.0001):
# 先创建一个与参数组等长的向量
res = np.empty(len(w))
# 对于每个梯度,求值
for i in range(len(w)):
w_1 = w.copy()
w_1[i] += epsilon
w_2 = w.copy()
w_2[i] -= epsilon
res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
return res
在这里,有一处需要注意的地方:
对于要求的轴,向量ω,实际上一个单位向量,即要让向量的模为1
因此我们使用np中的线性代数库linalg里面的norm()方法,求第二范数,也就是求算术平方根
def direction(w):
return w / np.linalg.norm(w)
然后就实现梯度上升代码的流程了:gradient_ascent()方法为梯度上升法的过程,在n_iters次循环中,每次获得新的ω,如果新的ω和旧的ω对应的函数f的值的差值满足精度epsilon,则表示找到了合适的 w w w:
此处要注意,对于每一次计算向量ω之前都要进行单位化计算,使其模为1。
# 梯度上升法代码
def gradient_ascent(df, X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = df_math(w,X)
last_w = w
w = last_w + eta * gradient
w = direction(w) # 将w转换成单位向量
if (abs(f(w,X) - f(last_w,X)) < epsilon):
break
cur_iter += 1
return w
接着使用梯度上升法,先设定一个初始的ω和学习率η :
这里面还需要注意一点:线性回归中,通常将特征系数θ的值设为全部为0的向量。但在主成分分析中w的初始值不能为0!!! 这是因为如果将w=0带入梯度求导的公式中,也是每次求梯度得到的都是没有任何方向的0。所以要设置一组随机数。
initial_w = np.random.random(X.shape[1])
eta = 0.001
然后执行gradient_ascent()方法,计算梯度上升的结果,即要求的轴。
w = gradient_ascent(df_debug, X_demean, initial_w, eta)
# 输出
array([0.76567331, 0.64322965])
3. 结果可视化
进行可视化,轴对应的方向,即将样本映射到该轴上的方差最大,这个轴就是一个主成分(第一主成分):
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([0,w[0]*30],[0,w[1]*30], color='red')
plt.show()

这样,就求出了二维数据的1个主成分,二维数据映射到一维就足够了。
但是如果是高维数据,可能就要映射到多维上。即求出第n主成分。
(三)求前n个主成分
1. 思想
在实际的降维过程可能会涉及到数据在多个维度的降维,这就需要依次求解多个主成分。
求解第一个主成分后,假设得到映射的轴为ω所表示的向量,如果此时需要求解第二个主成分怎么做?
答案是:需要先将数据集在第一个主成分上的分量去掉,然后在没有第一个主成分的基础上再寻找第二个主成分。
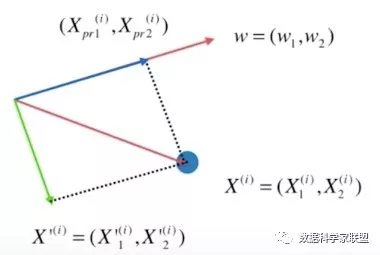
如上图所示,样本 X ( i ) X^{(i)} X(i)在第一主成分ω上的分量为 ( X p r 1 ( i ) , X p r 2 ( i ) ) (X_{pr1}^{(i)},X_{pr2}^{(i)}) (Xpr1(i),Xpr2(i)),也就是图中的蓝色向量,其模长是 X ( i ) X^{(i)} X(i)向量和ω向量的乘积,又因为ω是单位向量,向量的模长乘以方向上的单位向量就可以得到这个向量。
求下一个主成分就是将数据在第一主成分上的分量去掉,再对新的数据求第一主成分。
那么如何去掉第一主成分呢?用样本 X ( i ) X^{(i)} X(i)减去分量 ( X p r 1 ( i ) , X p r 2 ( i ) ) (X_{pr1}^{(i)},X_{pr2}^{(i)}) (Xpr1(i),Xpr2(i)),得到结果的几何意义就是一条与第一主成分垂直的一个轴。这个轴就是样本数据去除第一主成分分量后得到的结果,即图中的绿色部分: X ′ ( i ) = X ( i ) − ( X p r 1 ( i ) , X p r 2 ( i ) ) X^{'(i)}=X^{(i)}-(X_{pr1}^{(i)},X_{pr2}^{(i)}) X′(i)=X(i)−(Xpr1(i),Xpr2(i))。
然后在新的样本 X ′ ( i ) X^{'(i)} X′(i)中求第一主成分,得到的就是第二主成分。循环往复就可以求第n主成分。
2. 求第二主成分的实现
首先,我们要将数据集在第一个主成分上的分量去掉。即用样本 X ( i ) X^{(i)} X(i)减去样本在第一主成分分量上的映射,得到 X n e w X_{new} Xnew。
这里可以用向量化的思想:
- 矩阵X( m × n m\times n m×n的矩阵)与向量ω( 1 × n 1\times n 1×n的矩阵)点乘,得到的是一个 m × 1 m \times 1 m×1的向量,这m个元素表示X中的每一个样本映射到向量ω方向上的模长
- 然后对向量reshape,使其成真正的 m × 1 m\times 1 m×1的矩阵
- 再乘以ω,得到的矩阵 m × n m \times n m×n,也就是把矩阵中每个样本的每个维度在ω方向上的分量。即矩阵 X p r o j e c t X_{project} Xproject
- 用样本X减去样本在第一主成分上的映射
X_new = X - X.dot(w).reshape(-1,1) * w
X n e w X_{new} Xnew是什么样的,可以可视化看一下:
plt.scatter(X_new[:,0], X_new[:,1])
plt.show()
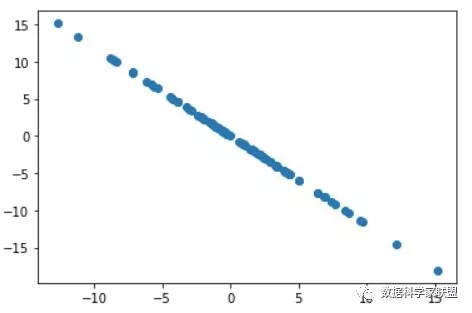
所有数据把第一主成分的分量去掉,得到的就是与第一主成分的分量垂直的向量。
由于整个数据只有两个维度,第一个维度去掉之后,剩下的第二维度就是所有的内容了。因此样本在第二维度上的分布完全在一条直线上,不再有其他方向上分布的方差。
如何第二主成分的轴?就是将去掉第一主成分的分量的 X n e w X_{new} Xnew带入到gradient_ascent()函数中,即可以得到新的轴 ω n e w ω_{new} ωnew。
w_new = gradient_ascent(df_math, X_new, initial_w, eta)
# 输出:
array([-0.64320916, 0.76569052])
ω 和 ω n e w ω和ω_{new} ω和ωnew彼此之间互相垂直,点乘为0。
3 求前n主成分
整合代码,first_n_component()方法用于求X的前n个主成分。
首先进行数据归零操作,使用列表res存储前n个主成分的方向向量。在for循环中每次求主成分时都设定一个随机的ω(initial_w),使用梯度上升法得到一个主成分后就去掉在这个主成分上的分量X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w:
def first_n_component(n, X, eta=0.001, n_iters=1e4, epsilon=1e-8):
X_pca = X.copy()
X_pca = demean(X_pca)
res = []
for i in range(n):
initial_w = np.random.random(X_pca.shape[1])
w = gradient_ascent(df_math, X_pca, initial_w, eta)
res.append(w)
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
return res
(四)小结
我们使用python对求主成分的思想进行了实现。首先求解了主成分的梯度表达式,然后通过梯度上升法来求得分量。在求解的时候有两个需要注意的地方。一是要在每次计算前对分量ω进行处理,使其变为模长为1的单位向量。再一个就是主成分分析中ω的初始值不能为0。
在二维数据中求得第一主成分分量就够了,对于高维数据需要先将数据集在第一个主成分上的分量去掉,然后在没有第一个主成分的基础上再寻找第二个主成分,依次类推,求出前n个主成分。最后我们整合代码。
三、降维映射及PCA的实现与使用
(一)高维数据向低维数据映射
在之前已经学习了如何求一个数据集的前n个主成分,但是数据集本身已经是n维的,并没有进行降维度。那么PCA是如何降维的呢?如何从高维数据向低维数据映射?
主成分分析的作用就是选出能使样本方差最大的维度,选择完维度之后,进入对数据降维的操作。将高维数据映射为低维数据。
假设经过主成分分析之后,左侧X还是数据样本,一个mn的矩阵,m个样本n个特征。根据主成分分析法求出了前k个主成分,得到矩阵W
,即有k个主成分向量,每个主成分的坐标系有n个维度(与转换前的维度相同),形成一个kn的矩阵。
X = ( X 1 ( 1 ) , X 2 ( 1 ) , … , X n ( 1 ) X 1 ( 2 ) , X 2 ( 2 ) , … , X n ( 2 ) … X 1 ( m ) , X 2 ( m ) , … , X n ( m ) ) , W k = ( W 1 ( 1 ) , W 2 ( 1 ) , … , W n ( 1 ) W 1 ( 2 ) , W 2 ( 2 ) , … , W n ( 2 ) … W 1 ( m ) , W 2 ( m ) , … , W n ( m ) ) X=\begin{pmatrix} X_1^{(1)},X_2^{(1)},…,X_n^{(1)}\\ X_1^{(2)},X_2^{(2)},…,X_n^{(2)}\\ …\\ X_1^{(m)},X_2^{(m)},…,X_n^{(m)}\end{pmatrix},W_k=\begin{pmatrix} W_1^{(1)},W_2^{(1)},…,W_n^{(1)}\\ W_1^{(2)},W_2^{(2)},…,W_n^{(2)}\\ …\\ W_1^{(m)},W_2^{(m)},…,W_n^{(m)}\end{pmatrix} X=⎝⎜⎜⎜⎛X1(1),X2(1),…,Xn(1)X1(2),X2(2),…,Xn(2)…X1(m),X2(m),…,Xn(m)⎠⎟⎟⎟⎞,Wk=⎝⎜⎜⎜⎛W1(1),W2(1),…,Wn(1)W1(2),W2(2),…,Wn(2)…W1(m),W2(m),…,Wn(m)⎠⎟⎟⎟⎞
如何将样本X从n维转换为k维呢?
对于一个样本 X 1 ( 1 ) X_1^{(1)} X1(1)来说,分别点乘W中的每一行( W i ( 1 ) , W i ( 2 ) , … , W i ( n ) , i ∈ ( 1 , k ) W_i^{(1)},W_i^{(2)},…,W_i^{(n)},i\in (1,k) Wi(1),Wi(2),…,Wi(n),i∈(1,k)),得到k个数,这k个数组成的向量。即表示将样本 X 1 ( 1 ) X_1^{(1)} X1(1)映射到了 W k W_k Wk这个坐标向量上,得到的新的k维向量,即完成了高维n到低维k的映射。对于每个样本,依次类推,就将所有样本从n维映射到k维。其实就相当于做一个矩阵乘法,得到一个m*k的矩阵(注意,这里需要转置):
X ⋅ W k T = X k X \cdot W_k^T=X_k X⋅WkT=Xk
在这个降维的过程中可能会丢失信息。如果原先的数据中本身存在一些无用信息,降维也可能会有降噪效果。
(二)PCA代码实现
定义一个类PCA,构造函数函数中n_components表示主成分个数即降维后的维数,components_表示主成分 W k W_k Wk ;
函数fit()与上面的first_n_component()方法一样,用于求出 W k W_k Wk;
函数transform()将X映射到各个主成分分量中,得到 W k W_k Wk,即降维;
函数transform()将 W k W_k Wk映射到原来的特征空间,得到 X m X_m Xm。
import numpy as np
class PCA:
def __init__(self, n_components):
# 主成分的个数n
self.n_components = n_components
# 具体主成分
self.components_ = None
def fit(self, X, eta=0.001, n_iters=1e4):
'''均值归零'''
def demean(X):
return X - np.mean(X, axis=0)
'''方差函数'''
def f(w, X):
return np.sum(X.dot(w) ** 2) / len(X)
'''方差函数导数'''
def df(w, X):
return X.T.dot(X.dot(w)) * 2 / len(X)
'''将向量化简为单位向量'''
def direction(w):
return w / np.linalg.norm(w)
'''寻找第一主成分'''
def first_component(X, initial_w, eta, n_iters, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if(abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iter += 1
return w
# 过程如下:
# 归0操作
X_pca = demean(X)
# 初始化空矩阵,行为n个主成分,列为样本列数
self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
# 循环执行每一个主成分
for i in range(self.n_components):
# 每一次初始化一个方向向量w
initial_w = np.random.random(X_pca.shape[1])
# 使用梯度上升法,得到此时的X_PCA所对应的第一主成分w
w = first_component(X_pca, initial_w, eta, n_iters)
# 存储起来
self.components_[i:] = w
# X_pca减去样本在w上的所有分量,形成一个新的X_pca,以便进行下一次循环
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
return self
# 将X数据集映射到各个主成分分量中
def transform(self, X):
assert X.shape[1] == self.components_.shape[1]
return X.dot(self.components_.T)
def inverse_transform(self, X):
return X.dot(self.components_)
(三)sklearn中的PCA
1.PCA的使用
- 首先准备数据:
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
- 然后fit一下,求出主成分
from sklearn.decomposition import PCA
# 初始化实例对象,传入主成分个数
pca = PCA(n_components=1)
pca.fit(X)
- 验证一下pca求出的主成分,是一个方向向量:
pca.components_
# 输出
array([[-0.76676934, -0.64192272]])
- 在得到主成分之后,使用transform方法将矩阵X进行降维。得到一个特征的数据集。
X_reduction = pca.transform(X)
X_reduction.shape
# 输出
(100,1)
2. 真实数据降维
为了验证PCA算法在真实数据中的威力,我们对手写数据集digits使用主成分分析法进行降维,再用kNN算法进行分类,观察前后的结果有何不同。
首先准备数据集:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
对原始数据集进行训练,看看识别的结果
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)
# 输出:
0.98666666666666669
下面用PCA算法对数据进行降维:
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train) # 训练数据集降维结果
X_test_reduction = pca.transform(X_test) # 测试数据集降维结果
下面使用降维后的数据,观察其kNN算法的识别精度:
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
# 输出:
0.60666666666666669
可以看到,数据由64维降到2维之后,精度也相应的降低了。那么我们具体应该降低到哪维呢?n_components参数如何设置?
3. 主成分解释方差比例
PCA算法提供了一个特殊的指标pca.explained_variance_ratio_(解释方差比例),我们可以使用这个指标找到某个数据集保持多少的精度:
pca.explained_variance_ratio_
# 输出:
array([ 0.14566817, 0.13735469])
上面就是主成分所解释的方差比例。对于现在的PCA算法来说,得到的是二维数据:0.14566817表示第一个轴能够解释14.56%数据的方差;0.13735469表示第二个轴能够解释13.73%数据的方差。PCA过程寻找主成分,就是找使得原数据的方差维持的最大。这个值就告诉我们,PCA最大维持了原来所有方差的百分比。对于这两个维度来说,[ 0.14566817, 0.13735469]涵盖了原数据的总方差的28%左右的信息,剩下72%的方差信息就丢失了,显然丢失的信息过多。
下面我们使用PCA算法保持数据64维:
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_
array([1.45668166e-01, 1.37354688e-01, 1.17777287e-01, 8.49968861e-02,
5.86018996e-02, 5.11542945e-02, 4.26605279e-02, 3.60119663e-02,
3.41105814e-02, 3.05407804e-02, 2.42337671e-02, 2.28700570e-02,
1.80304649e-02, 1.79346003e-02, 1.45798298e-02, 1.42044841e-02,
1.29961033e-02, 1.26617002e-02, 1.01728635e-02, 9.09314698e-03,
8.85220461e-03, 7.73828332e-03, 7.60516219e-03, 7.11864860e-03,
6.85977267e-03, 5.76411920e-03, 5.71688020e-03, 5.08255707e-03,
4.89020776e-03, 4.34888085e-03, 3.72917505e-03, 3.57755036e-03,
3.26989470e-03, 3.14917937e-03, 3.09269839e-03, 2.87619649e-03,
2.50362666e-03, 2.25417403e-03, 2.20030857e-03, 1.98028746e-03,
1.88195578e-03, 1.52769283e-03, 1.42823692e-03, 1.38003340e-03,
1.17572392e-03, 1.07377463e-03, 9.55152460e-04, 9.00017642e-04,
5.79162563e-04, 3.82793717e-04, 2.38328586e-04, 8.40132221e-05,
5.60545588e-05, 5.48538930e-05, 1.08077650e-05, 4.01354717e-06,
1.23186515e-06, 1.05783059e-06, 6.06659094e-07, 5.86686040e-07,
7.44075955e-34, 7.44075955e-34, 7.44075955e-34, 7.15189459e-34])
训练数据集是一个含有64个特征的数据集,经过主成分分析得到的explained_variance_ratio_也是一个含有64个元素的数据集,表示每个主成分对原始数据方差的解释度。从结果可以看出,所占方差的比例是一个从大到小的排列。第一个轴占了14.56%,最后几个的解释度几乎为零,也就是说对原始方差基本没有作用,完全可以忽略不计。也就是说可以将主成分所解释的方差比例视为重要程度。
这种方式虽然耗时增加了,但分类的准确度提高了。在实际情况下,可能会忽略对原始方差影响小的成分,在时间和准确度之间做一个权衡。因此我们可以绘制下面的折线图:
# 横轴是是样本X的i个特征数,纵轴是前i个轴解释方差比例的和
plt.plot([i for i in range(X_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()
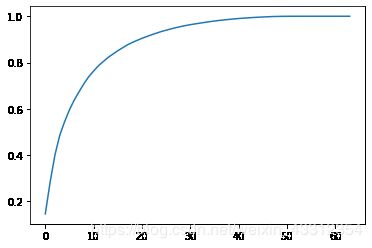
如果我们希望保持95%以上的信息,就能得到相应的降维后的主成分个数。在sklearn中,实例化时传入一个数字,就表示保持的方差比例:
pca = PCA(0.95)
pca.fit(X_train)
# 输出:
PCA(copy=True, iterated_power='auto', n_components=0.95, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
查看一下降维后主成分的个数为28,即对于64维数据来说,28维数据就可以解释95%以上的方差。
pca.n_components_
# 输出:
28
然后用这种pca去重新使用kNN做训练,得到的结果较好。
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
# 输出
0.98
数据降维还有一个作用是可视化,降到2维数据之后:
pca = PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X)
for i in range(10):
plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)
plt.show()
(四)小结
PCA法是通过选出使样本方差最大的维度来求主成分的。那么确定了主成分的方向向量后,就需要将高维数据向低维数据映射。方法就是将样本分别点乘每一个主成分向量(数),得到k个数并组成向量。以此类推,完成高维n到低维k的映射。其公式为: X ⋅ W k T = X k X\cdot W_k^T=X_k X⋅WkT=Xk
我们在使用sklearn中提高的PCA方法时,需要先初始化实例对象(此时可以传递主成分个数),fit操作得到主成分后进行降维映射操作pca.transform。在初始化实例对象时,也可以传入一个数字,表示主成分所解释的方差比例,即每个主成分对原始数据方差的重要程度。忽略对原始方差影响小的成分,在时间和准确度之间做一个权衡。
四、数据降维之应用:降噪&人脸识别
(一)应用数据降噪
1. 为什么PCA能降噪
在实际的数据中不可避免地出现各种噪音,这些噪音的出现可能会对数据的准确性造成一定的影响。而主成分分析法还有一个用途就是降噪。PCA通过选取主成分将原有数据映射到低维数据再映射回高维数据的方式进行一定程度的降噪。
例如,我们构造一组数据:
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 5, size=100)
plt.scatter(X[:,0], X[:,1])
plt.show()
其中np.random.normal(0, 5, size=100)就是我们认为添加的噪声,在线性方程上下抖动。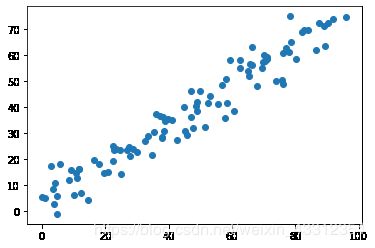
我们降噪,这就需要使用PCA中的一个方法:X_ori=pca.inverse_transform(X_pca),将降维后的数据转换成与维度相同数据。要注意,还原后的数据,不等同于原数据!
这是因为在使用PCA降维时,已经丢失了部分的信息(忽略了解释方差比例)。因此在还原时,只能保证维度相同。会尽最大可能返回原始空间,但不会跟原来的数据一样。
这样一来一回之间,丢失掉的信息,就相当于降噪了。
在Stack Overflow中找到了两个不错的答案:
- you can only expect this if the number of components you specify is the same as the dimensionality of the input data. For any
n_components less than this, you will get different numbers than the
original dataset after applying the inverse PCA transformation: the
following diagrams give an illustration in two dimensions.
- It can not do that, since by reducing the dimensions with PCA, you’ve
lost information (check pca.explained_variance_ratio_ for the % of
information you still have). However, it tries its best to go back to
the original space as well as it can, see the picture below
对制造的数据先降维,后还原,就可以去除噪音了:
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)
plt.scatter(X_restore[:,0], X_restore[:,1])
plt.show()

transform降维成一维数据,再inverse_transform返回成二维数据。此时数据成为了一条直线。这个过程可以理解为将原有的噪音去除了。
当然,我们丢失的信息也不全都是噪音。我们可以将PCA的过程定义为:
降低了维度,丢失了信息,也去除了一部分噪音。
2. 手写数字降噪实例
重新创建一个有噪音的数据集,以digits数据为例:
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target
# 添加一个正态分布的噪音矩阵
noisy_digits = X + np.random.normal(0, 4, size=X.shape)
# 绘制噪音数据:从y==0数字中取10个,进行10次循环;
# 依次从y==num再取出10个,将其与原来的样本拼在一起
example_digits = noisy_digits[y==0,:][:10]
for num in range(1,10):
example_digits = np.vstack([example_digits, noisy_digits[y==num,:][:10]])
example_digits.shape
# 输出:
(100, 64) # 即含有100个数字(0~9各10个),每个数字有64维
下面将这100个数字绘制出来,得到有噪音的数字:
def plot_digits(data):
fig, axes = plt.subplots(10, 10, figsize=(10, 10),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plt.show()
plot_digits(example_digits)
下面使用PCA进行降噪:
pca = PCA(0.5).fit(noisy_digits)
pca.n_components_
# 输出:12,即原始数据保存了50%的信息,需要12维
# 进行降维、还原过程
components = pca.transform(example_digits)
filtered_digits = pca.inverse_transform(components)
plot_digits(filtered_digits)
(二)人脸识别
PCA将样本X从n维空间映射到k维空间,求出前k个主成分, X ⋅ W k T = X k X\cdot W_k^T=X_k X⋅WkT=Xk。一个 m ∗ n m*n m∗n的矩阵,在经过主成分分析之后,一个 k ∗ n k*n k∗n的主成分矩阵。如果将主成分矩阵也看成是由k个样本组成的矩阵,那么可以理解为第一个样本是最重要的样本,以此类推。
在人脸识别领域中,原始数据矩阵可以视为有m个人脸样本的集合,如果将主成分矩阵每一行也看做是一个样本的话,每一行相当于是一个由原始人脸数据矩阵经过主成分分析得到的“特征脸”(Eigenface)矩阵,这个矩阵含有k个“特征脸”。每个“特征脸”表达了原有样本中人脸的部分特征。
1. 展示数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people()
faces.keys()
# 输出:dict_keys(['data', 'images', 'target', 'target_names', 'DESCR'])
faces.data.shape
# 输出:(13233, 2914)
# images属性,即对每一维样本,将其以2维的形式展现出来
# 即对于每个样本来说都是62*47
faces.images.shape
# 输出:(13233, 62, 47)
random_indexes = np.random.permutation(len(faces.data))
X = faces.data[random_indexes]
example_faces = X[:36,:]
example_faces.shape
# 输出:(36, 2914)
# 一万多张脸 抽出36张脸
def plot_faces(faces):
fig, axes = plt.subplots(6, 6, figsize=(10, 10),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(faces[i].reshape(62, 47), cmap='bone')
plt.show()
plot_faces(example_faces)
- 首先,看一下下载的目录,将这个包(lfw_funneled.tgz)被下载到了这个文件夹下面:/Users/your_name/scikit_learn_data/lfw_home/
- 把下载之前下载的文件lfw_funneled删除。(如果已经解压出文件夹,也把这个文件夹删除)
- 同时复制这个网址 https://ndownloader.figshare.com/files/5976015 到迅雷中,下载到完整的lfwfunneded.tgz文件。并把这个文件复制到/Users/your_name/scikit_learn_data/lfw_home/下面,并解压缩。重新加载代码即可。
2. 特征脸
from sklearn.decomposition import PCA
%%time
# 实例化PCA,求出所有的主成分
pca = PCA(svd_solver='randomized')
pca.fit(X)
输出所有的主成分(向量)以及每个主成分的特征
pca.components_.shape
# 输出:(2914, 2914)
特征脸就是主成分中的每一行都当作一个样本,排名越靠前,表示该特征脸越能表示人脸的特征。取出前36个特征脸进行可视化:
plot_faces(pca.components_[:36, :])
(三)小结
主成分分析法(PCA)的一些应用场景,除了降维以外,还可以进行降噪以及特征提取,也可以用作异常点检测。
总之,PCA算法在机器学习领域中有非常广泛的应用,需要好好领悟其思想和原理,在应用中才会游刃有余。





