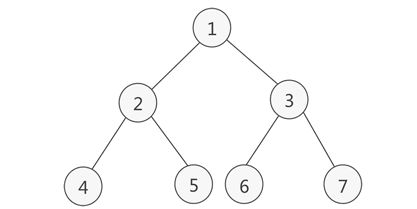
二叉树是我们常见的数据结构之一,在学习二叉树之前我们需要知道什么是树,什么是二叉树,本篇主要讲述了二叉树,以及二叉树的遍历。
你能get到的知识点?
1、树的介绍
2、二叉树的介绍
3、二叉树遍历的四种方法
4、牛客题目:反转二叉树
- 你能get到的知识点?
- 一、知识预备
- 1、树
- 2、树的相关术语介绍
- 1、二叉树
- 2、二叉树类型
- 二、二叉树实操(我没有说脏话)
- 1、定义二叉树的结点
- 2、遍历二叉树(四种方法)
- 三、小试牛刀
- leetcode题目:反转二叉树
一、知识预备
1、树
树(Tree)是n(n>=0)个结点的有限集。
数据结构中的树可以看作一个倒立的树,他的‘根’在上面,他的'叶子'在下面。
2、树的相关术语介绍
- 1、树的结点(node):包含一个数据元素及若干指向子树的分支;
- 2、孩子结点(child node):结点的子树的根称为该结点的孩子,对于结点4来说,结点2和结点7就是结点4的孩子结点;
- 3、双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
- 4、兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
- 5、祖先结点: 从根到该结点的所经分支上的所有结点
- 6、子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙
- 7、结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
- 8、树的深度:树中最大的结点层,该树的深度为三,因为他只有三层。
- 9、结点的度:结点子树的个数
- 10、树的度: 树中最大的结点度。
- 11、叶子结点:也叫终端结点,是度为 0 的结点,例如结点1、2、6、9,都是叶子结点;
- 12、分枝结点:度不为0的结点;
- 13、有序树:子树有序的树,如:家族树;
- 14、无序树:不考虑子树的顺序;
1、二叉树
二叉树(Binary Tree)是每个结点最多有两个子树的树结构。所以二叉树也是一种特殊的树。
通常我们将二叉树的子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
二叉树常被用于实现二叉查找树和二叉堆。

由此可以看出,一棵二叉树,他的每个节点最多只有两个结点,也就是结点的度小于等于二,即取0、1、2。
2、二叉树类型
-
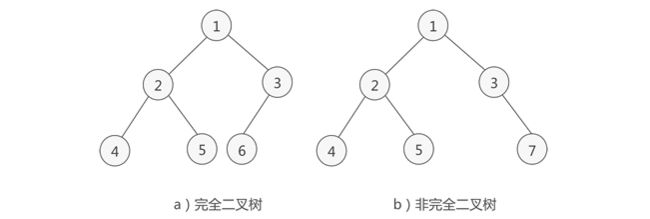
完全二叉树:若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
简单来说:如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
-
平衡二叉树:平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
二、二叉树实操(我没有说脏话)
1、定义二叉树的结点
定义二叉树每一个节点的结构,他拥有左右子叶,并且本身拥有一个值val,定义一个构造函数,多个结点组合在一起就是一个二叉树。
/**
* Definition for binary tree
*/
public static class TreeNode {
//定义该结点值
int val;
//定义左结点
TreeNode left;
//定义右结点
TreeNode right;
//定义一个构造函数
TreeNode(int x) { val = x; }
}
例图:以下将以该例图进行解说
2、遍历二叉树(四种方法)
遍历二叉树主要有四种方法:①:前序遍历 ②:中序遍历 ③:后序遍历 ④:层序遍历
需要事先说明的就是前三种遍历,就是根节点的访问顺序不同,但是访问左右节点的顺序仍然是先访问左结点,再访问右结点。
①:前序遍历
1、访问根节点;
2、访问当前节点的左子树;
3、访问当前节点的右子树;
就是先从根节点出发,先访问根节点,然后访问根结点的左子树,若该左子树的根节点上存在左子树,则访问其左子树,否则,访问其右子树,依次类推。
以上图为例,
- 先找到根节点,读取4,
- 该结点还有左子树,访问其左子树的根节点,读取2,
- 结点2,还有左子树,读取1,
- 结点1没有左子树也没有右子树,返回上一层,访问结点2的右子树,读取3,
- 这时候应该访问3的左右子树,但是没有,返回上一层,此时结点2的左右子树都已经读取完,返回上一层,读取结点4的右子树,读取7,
- 访问结点7的左子树,读取6,
- 结点6没有左右子树,返回上一层,访问结点7的右子树,读取9,
- 结点9没有左右子树,这时候该二叉树已经遍历完成。
所以访问到的顺序为:4 2 1 3 7 6 9
②:中序遍历
1、访问当前节点的左子树;
2、访问根节点;
3、访问当前节点的右子树;
遍历思想与前序差不多,只不过将读取根节点放在读取左结点之后、右结点之前
③:后序遍历
1、访问当前节点的左子树;
2、访问当前节点的右子树;
3、访问根节点;
遍历思想与前序差不多,只不过将读取根节点放在读取左结点之后、右结点之后
④:层序遍历
按照二叉树的层级结构从左至右依次遍历结点
算法思路:定义一个队列,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
- 根节点4入队,
- 根节点4出队,访问结点4的左右结点(2,7),依次入队,
- 结点2出队,访问结点2的左右结点(1,3),依次入队,
- 结点1出队,无子结点,无需入队,
- 结点3出队,无子结点,无需入队,
- 结点6出队,无子结点,无需入队,
- 结点9出队,无子结点,无需入队,
- 队列为空,遍历完成。
最后访问顺序为:4 2 7 1 3 6 9
代码实现:
/**
* 先序遍历(递归)
* @param node
*/
public void previous(TreeNode node) {
if (node == null) {
return;
}
System.out.print(node.val+"\t");
this.previous(node.left);
this.previous(node.right);
}
/**
* 中序遍历(递归)
* @param node
*/
public void middle(TreeNode node) {
if (node == null) {
return;
}
this.middle(node.left);
System.out.print(node.val+"\t");
this.middle(node.right);
}
/**
* 后序遍历(递归)
* @param node
*/
public void next(TreeNode node) {
if (node == null) {
return;
}
this.next(node.left);
this.next(node.right);
System.out.print(node.val+"\t");
}
/**
* 遍历二叉树
* 层序遍历(非递归)
* @param node
*/
public void bfs(TreeNode node){
if (node == null) {
return;
}
Queue queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()){
TreeNode current = queue.poll();
System.out.print(current.val + "\t");
//如果当前节点的左节点不为空入队
if(current.left != null)
{
queue.offer(current.left);
}
//如果当前节点的右节点不为空,把右节点入队
if(current.right != null)
{
queue.offer(current.right);
}
}
}
遍历结果:
1、前序遍历:4 2 1 3 7 6 9
2、中序遍历:1 2 3 4 6 7 9
3、后序遍历:1 3 2 6 9 7 4
4、层序遍历:4 2 7 1 3 6 9
在这里附上前三种方法的非递归方法,感兴趣的小伙伴可以研究研究。
附:非递归方法
主要实现是依靠栈来实现
/**
* 先序遍历非递归
* @param node
*/
public void previous1(TreeNode node) {
if (node == null) {
return;
}
Stack queue = new Stack<>();
queue.add(node);
while (!queue.isEmpty()) {
TreeNode current = queue.pop();
while(current!=null) {
System.out.print(current.val + "\t");
if (current.right!=null){
queue.push(current.right);
}
current = current.left;
}
}
}
/**
* 中序遍历(非递归)
* @param node
*/
public void middle1(TreeNode node) {
Stack stack = new Stack<>();
while (!stack.isEmpty() || node !=null) {
while (node != null){
stack.push(node);
node = node.left;
}
node = stack.pop();
System.out.print(node.val + "\t");
node = node.right;
}
}
/**
* 后序遍历(非递归)
* @param node
*/
public void next1(TreeNode node) {
Stack stack = new Stack<>();
Stack stack1 = new Stack<>();
while (!stack.isEmpty() || node !=null) {
while (node != null){
stack.push(node);
stack1.push(0);
node = node.left;
}
while (!stack.isEmpty() && stack1.peek() == 1) {
stack1.pop();
System.out.print(stack.pop().val + "\t");
}
if (!stack.isEmpty()) {
stack1.pop();
stack1.push(1);
node = stack.peek();
node = node.right;
}
}
}
三、小试牛刀
leetcode题目:反转二叉树
原来的二叉树:
经过算法,需要转换为:
解法:
二叉树的遍历有四种方法,那么,该题解法也至少有四种,如果读懂了上面的遍历算法,那么这道题简直轻而易举。
主要思路:就是遍历某一结点时,也就是在原来输出该节点的操作换成将其结点的左右结点交换位置。
/**
* 反转二叉树
* 前序反转
* @param node
*/
public void invertTree_previous(TreeNode node){
if (node == null){
return;
}
TreeNode node1 = node.left;
node.left = node.right;
node.right = node1;
this.invertTree_previous(node.left);
this.invertTree_previous(node.right);
}
/**
* 反转二叉树
* 中序反转
* @param node
*/
public void invertTree_middle(TreeNode node){
if (node == null){
return;
}
this.invertTree_middle(node.left);
TreeNode node1 = node.left;
node.left = node.right;
node.right = node1;
this.invertTree_middle(node.left);
}
/**
* 反转二叉树
* 后序序反转
* @param node
*/
public void invertTree_next(TreeNode node){
if (node == null){
return;
}
this.invertTree_next(node.left);
this.invertTree_next(node.right);
TreeNode node1 = node.left;
node.left = node.right;
node.right = node1;
}
/**
* 反转二叉树
* 层序反转
* @param node
*/
public void invertTree_bfs(TreeNode node){
if (node == null) {
return;
}
Queue queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()){
TreeNode current = queue.poll();
TreeNode node1 = current.left;
current.left = current.right;
current.right = node1;
//如果当前节点的左节点不为空入队
if(current.left != null)
{
queue.offer(current.left);
}
//如果当前节点的右节点不为空,把右节点入队
if(current.right != null)
{
queue.offer(current.right);
}
}
}
答案:
1、转换前
前序遍历:4 2 1 3 7 6 9
中序遍历:1 2 3 4 6 7 9
后序遍历:1 3 2 6 9 7 4
层次遍历:4 2 7 1 3 6 9
2、转换后
前序遍历:4 7 9 6 2 3 1
中序遍历:9 7 6 4 3 2 1
后序遍历:9 6 7 3 1 2 4
层次遍历:4 7 2 9 6 3 1
源码获取:关注公众号:博奥思园,回复:数据结构二叉树
你的支持是我前进的最大动力
参考:
1、 Java数据结构和算法(十)——二叉树
2、二叉树的四种遍历算法
3、Java实现二叉树的前序、中序、后序、层序遍历(非递归方法)