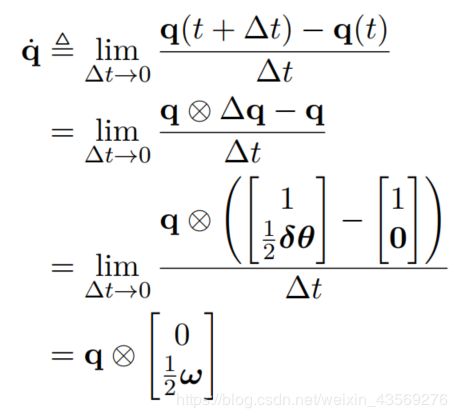SLAM基础——四元数(含四元数对时间的导数)
1.四元数
SLAM中的旋转矩阵 R \mathrm{R} R 可以用四元数 q q q 来表示
单位四元数可表达任意三维旋转,且无奇异性。
一个四元数 q q q 具有一个实部和三个虚部。将实部写在前,虚部写在后,则有:
q = [ q 0 , q 1 , q 2 , q 3 ] T 或 q = [ w , x , y , z ] T q=[q_0,q_1, q_2, q_3]^T \ 或 \ q=[w,x,y,z]^T q=[q0,q1,q2,q3]T 或 q=[w,x,y,z]T 其中 q 0 q_0 q0 是实部,为标量; [ q 1 , q 2 , q 3 ] T [q_1, q_2, q_3]^T [q1,q2,q3]T 是虚部,为矢量。
则四元数也可以记作:
q = [ s , v ] T q=[s, \bold{v}]^T q=[s,v]T 其中 s s s为标量, v \bold{v} v 为虚部的矢量。
2.四元数的性质
四元数的乘法:
两个四元数相乘,结果还是四元数,结果如下:
q a ⊗ q b = [ w a , x a , y a , z a ] T ⊗ [ w b , x b , y b , z b ] T = [ s a s b − v a T v b , s a v b + s b v a + v a × v b ] T = [ w a w b − x a x b − y a y b − z a z b w a x b + x a w b + y a z b − z a y b w a y b − x a z b + y a w b + z a x b w a z b + x a y b − y a x b + z a w b ] \begin{aligned} q_a \otimes q_b &= [w_a,x_a,y_a,z_a]^T \otimes [w_b,x_b,y_b,z_b]^T \\ &= [s_a s_b - \mathrm{v_a}^T \mathrm{v_b}, s_a \mathrm{v_b} + s_b \mathrm{v_a} + \mathrm{v_a} \times \mathrm{v_b}]^T \\ & = \begin{bmatrix} w_a w_b - x_a x_b - y_a y_b - z_a z_b \\ w_a x_b + x_a w_b + y_a z_b - z_a y_b \\ w_a y_b - x_a z_b + y_a w_b + z_a x_b \\ w_a z_b + x_a y_b - y_a x_b + z_a w_b \end{bmatrix} \end{aligned} qa⊗qb=[wa,xa,ya,za]T⊗[wb,xb,yb,zb]T=[sasb−vaTvb,savb+sbva+va×vb]T=⎣⎢⎢⎡wawb−xaxb−yayb−zazbwaxb+xawb+yazb−zaybwayb−xazb+yawb+zaxbwazb+xayb−yaxb+zawb⎦⎥⎥⎤
3.四元数与轴角的关系
假设某个旋转运动的旋转轴为单位向量 u \mathrm{u} u,绕该轴旋转的角度为 θ \theta θ,那么它对应的单位四元数为:
q = [ c o s θ 2 u s i n θ 2 ] q=\begin{bmatrix} cos{\frac{\theta}{2} } \\ \mathrm{u} sin{\frac{\theta}{2} }\end{bmatrix} q=[cos2θusin2θ] 当旋转一段微小的时间,即旋转角度趋于零时,容易有:

其中 δ θ \delta \theta δθ 的方向表示旋转轴,模长表示旋转角度。
4.四元数的导数
5.利用李代数进行旋转求导
使用旋转矩阵 R 时,角速度为 ω,那么 R 相对于时间的导数可写作:

该式被称为泊松公式(Possion’s equation),其中 ∧ 为反对称矩阵算子: