遗传算法求解函数最小值问题

遗传算法求解函数最小值问题

继上一次用遗传算法求解TSP问题问题以后，万万没有想到，实验的时候，老师居然改了题目，改成了求解函数的最小值问题（有点坑哈），而且要求结果尽量的稳定，可以确定得到最小值，并且，精度尽可能的高……虽然有点坑，不过老师还是简单的说明了一下基本的思路，思路和上一次没有太大的变化，唯一的难点就是怎样尽可能的提高解的精度。
不管怎样，终究在实验课的时候解决了这个问题，唯一的问题就是进度最多10的负六次方，老师说他的精度可以达到10的负几百次方（膜拜……）。
思路不变，选择用轮盘赌，变异要稍微变一下，具体会在下面讲解，废话少说，进入正题。.

问题描述：

设计高效遗传算法，求解下列函数在-5<=x1,x2<=5上的最小值：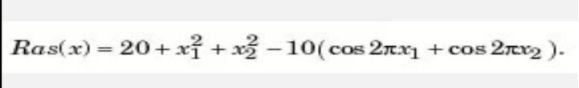
在正式的开始求解之前，老师先将函数的图片展示了出来，如下图所示：
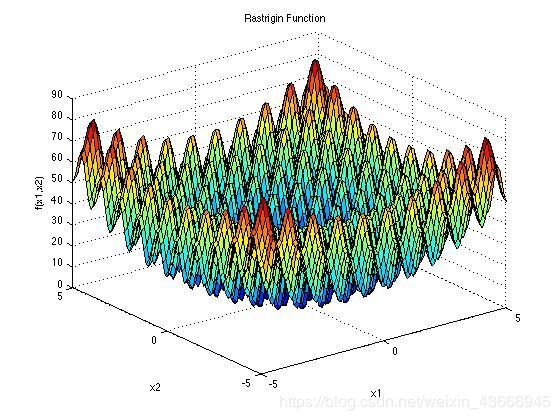并且公布结果，在（0,0）的位置取得最小值0。
在这个结果的基础上，我们开始试验。

代码编写：

首先是个体的类代码：

class problem1_individual(object):
    def __init__(self, n1, n2):
        self.gene = [n1, n2]
        self.score = 0
    pass

接着轮盘赌选择的代码，和上一次没有多少变化，同样是采用倒数的方式来作为个体的适配值，因为事先知道结果的最小值为0，所以采用倒数的方式很好，因为越接近0，倒数越大，被选中的概率就越大。
代码如下所示：

def roulette_wheel(self):
    """
    轮盘赌普通方法得到被选中的基因型
    :param individuals: 种群中各个基因类型的数量
    :return: 返回被选中的基因型的代号
    """
    all_individual = 0
    for i in range(len(self.list)):
        all_individual += 1 / self.list[i].score
    probabilities = []
    for i in range(len(self.list)):
        probabilities.append((1 / self.list[i].score) / all_individual)
    selected_individual = random.uniform(0, 1)
    now_individual = 0.0
    for ind, val in enumerate(probabilities):
        now_individual += val
        if now_individual > selected_individual:
            return self.list[ind]

接着是交叉的代码。在编写之前还没有办法，个体是两个自变量，但是交叉怎么办？上网查了一下，有了思路，很简单，就是用不同的比例进行划分。
随机生成一0-1的数字，作为其中一个父个体的基因比例，再用1减去这个数字，得到另一个父个体的基因比例，两者相加得到的就是最后的孩子的基因序列：

def crossgene(self, parent1, parent2, index1, index2):
    child = [0, 0]
    child[0] = parent1.gene[0] * index1 + parent2.gene[0] * index2
    child[1] = parent1.gene[1] * index1 + parent2.gene[1] * index2
    return child

def crossover(self, father, mother):
    """
    :param father: 需要进行遗传的父类个体
    :param mother: 需要进行遗传的母类个体
    :return:
    """
    x = random.randint(0, 9999)
    # 变异有概率，大于某个值就不发生，小于某个值就发生变异
    k = 10000 * self.variationrate
    if x < k:
        # 进行单点交换
        index1 = random.uniform(0, 1)
        index2 = 1 - index1
        child1 = self.crossgene(father, mother, index1, index2)
        child2 = self.crossgene(mother, father, index1, index2)
    else:
        child1 = father.gene
        child2 = mother.gene
    return child1, child2

结果测试：

代码编写完毕，现在进行测试，看看结果如何：

from problem1_GA import problem1_GA

test = problem1_GA(1, 1)
test.initpopulation()
for i in range(10000):
    test.next_generation()
    generation, answer, score = test.get_what_we_need()
    print(str(answer[0])+" "+str(answer[1])+" "+str(score))
    print()
    pass

迭代次数就采用10000次，看看最后的结果达到什么样的精度：

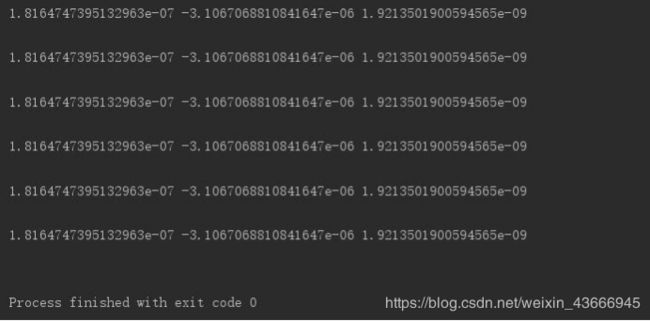
运气不错，最后的结果精度可以达到10^-9次方的水平。当然这次是运气好，但是不是每一次都可以重现这种操作，我还会继续的进行代码的优化，下一次让结果有更好的精度。
当然这都是后话。
最后完整的代码就放在以下链接中
遗传算法求解函数最小值问题
提取码：v2y6
还有上一次的文章缺少的CSDN链接，是tomcat的安装包和eclipse插件：
CSDN—tomcat
谢谢大家阅读！