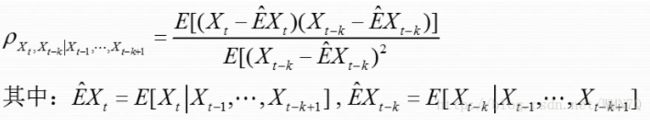统计模型总结1：时间序列分析及Python建模

时间序列分析是针对时间序列数据进行预测分析的一门学科，其不考虑其他因素的影响，只考虑预测对象随时间的变化，并据此作出预测分析。相对应的随机过程理论考虑的是随时间变化的一族随机变量全体。在工程应用中由于难以收集到全部的随机变量，随机过程理论一般较难应用。时间序列分析由于其只考虑预测分析的对象，在工程实践中较常得到应用。不过当对观察对象有很大影响的外界因素发生变化时，时间序列分析的预测结果误差较大。

1. 时间序列数据的预处理

在建立时间序列模型之前,必须先对时间序列数据进行必要的预处理,以便剔除那些不符合统计规律的异常样本,并对这些样本数据的基本统计特性进行检验,以确保建立时间序列模型的可靠性和置信度,并满足一定的精度要求。

1.1 时间序列的平稳性

一般说来,某个实测过程如果它的系统参数和运行时周围的条件不改变,即可视为平稳的。对于时间序列的平稳性，必须考虑以下两个内容:一是序列的均值u和方差σ是否为常数,二是序列的自相关函数acf是否仅与时间间隔有关,而与此间隔端点位置无关。
ARIMA等自回归类型的时间序列模型对于时间序列数据的平稳性有一定要求。对于时间序列数据的平稳性检验，一般可以使用扩展迪基-福勒检验（Augmented Dickey-Fuller test），即单位根检验ADF。单位根检验的原假设是检验序列中存在单位根，若存在单位根则序列是非平稳时间序列。已有证明，序列中存在单位根程就不平稳，会使回归分析中存在伪回归。
statsmodels中有专门用于adf检验的方法，该adf检验提供统计量、拒绝域以及p值，为了方便直接通过p值来判断时间序列的平稳性。

from statsmodels.tsa.stattools import adfuller
adf = adfuller(metric)    #if adf[1] < 0.05 then stationary

1.2 时间序列的趋势项与差分

时间序列不平稳的原因拆分开来其中一项就是因为时间序列包含趋势项。非平稳序列可以通过差分操作来消除趋势项，进而将非平稳序列转化为平稳序列。差分操作就是将每个时间点的值减去前一个时间点的值，需要注意的是每做一次差分，数据就会少一项。
差分： diff(x)=(x₂-x₁, x₃-x₂, …x_n-x_n-1)

metric = metric1.diff()

需要注意的是，在数据预处理过程中对数据进行了差分，需要在时间序列分析预测后进行逆差分还原。

在这里插入代码片

1.3 时间序列的季节项与季节差分

时间序列不平稳的原因拆分开来另一项就是因为时间序列包含季节项。非平稳序列可以通过季节差分操作来消除季节项，进而将非平稳序列转化为平稳序列。季节差分的季节周期较难确定，一般可以应用启发式方法来寻找。
季节差分： diff(x)=(x_n+1-x₁, x_n+2-x₂, …x_n+m-x_m)

df.diff(periods=n)

同样，在数据预处理过程中对数据进行了季节差分，需要在时间序列分析预测后进行季节逆差分还原。

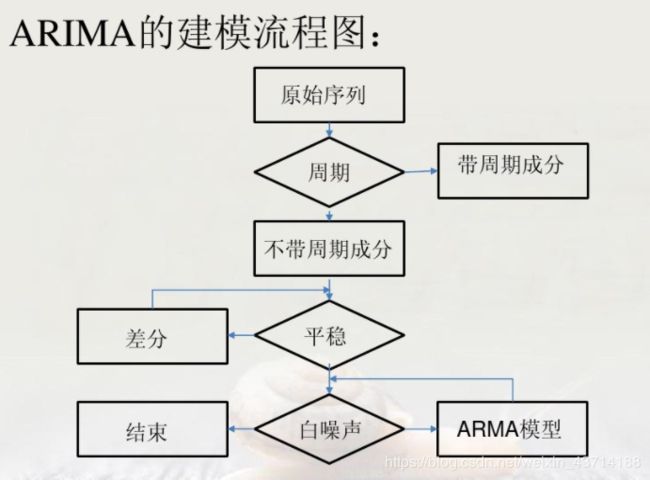
2 ARIMA时间序列模型体系

时间序列模型是描述时间序列统计特性的一种常用方法,在数学上就是用随机差分方程来表示时间序列模型的结构。它在时域上的解就是时间序列的自相关特 性,而在频域上的解就是时间序列的功率谱特性。这是分析时间序列最重要的两个性能,正如在研究随机过程的时域和频域特性那样,在实际应用中非常重要。

2.1 AR/MA/ARMA/ARIMA

当平稳的时间序列数据服从p阶的自回归过程，可以用自回归模型AR（p）来建模：

当平稳的时间序列数据等于白噪声序列的加权和，则该时间序列服从q阶的移动平均过程，可以通过移动平均模型MA（q）来建模：

当平稳的时间序列数据即包含数据之间的自相关行为又包含随机变动项的影响，综合AR与MA模型建立ARMA模型则更为有效与常用。自回归移动平均模型ARMA（p，q）为：

在现实的应用场景中，大多数时间序列数据为非平稳的，即他们的均值与方差随时间而变化。此时可以通过差分将非平稳的时间序列数据转化为平稳的时间序列数据。差分即是将相邻时间点的指标数值相减。

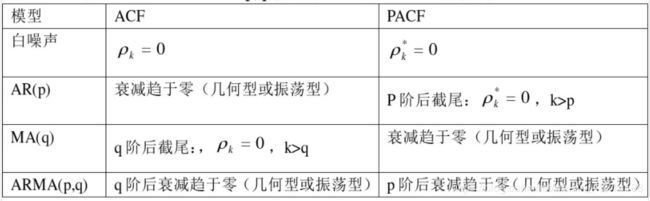
2.2 随机时间序列的ARIMA模型识别

随机时间序列模型的识别就是针对于一个平稳的随机事件序列，找出生成它的合适的随机过程或模型。在这里是指判断该时间序列是遵循纯AR过程还是遵循纯MA过程或ARMA过程。这里需要使用到时间序列的自相关函数ACF以及偏相关函数PACF。
自相关系数ACF定义如下：

偏相关系数PACF定义如下：

ARIMA模型识别方法：

2.4 时间序列模型ARIMA的参数估计

（1）矩估计

模型参数的相关矩估计是最常用的方法, 虽然它的估计精度不像经过优化处理后的估计方法那样高, 但它的算法方便实用。特别是对于具有正态性的时间序列, 在样本数据足 够多的情况下其估计精度可以与其他最佳估计算法相当。

（2）最小二乘估计

最小二乘估计是常用的最佳估计算法,相对于矩估计来说它属于精估计之一。它采用最小二乘的定义,使残差平方和达到最小,这时估计得到的模型参数就是最佳参数。

（3）最小方差估计

最小方差估计与最小二乘估计一样是一种精估计方法,但它们的最优化定义不同。最小方差估计是使真值与估值之间的平方误差期望值达到最小,亦即此时在最小方差定义下的平方和函数为最小,相应的最佳参数估值为最佳参数。

（4）最大似然估计

最大似然估计是利用样本数据序列的似然函数或者它的对数值达到最大。它的物理概念比较清楚,因为只有在选择最佳的模型参数情况下,才能做到时间序列模型所产生的数据序列与真实的实测数据序列相当接近,也就是模型的残差方差最小,模型的精度最好。

（5）最大熵估计

最大熵估计是利用信息论中关于信息熵的概念,因为如果时间序列模型的信息熵最 大,则就意味着模型数据与实测数据之间的残差方差最小,因此在这个意义下所选择的模型参 数应该是最佳的。
前面讨论过的几种最优化方法,对于具有正态性的时间序列模型来说,在数据总量 N 足够大的情况下可以获得相同或近似的模型参数,并且与没有采用优化的相关矩估计结果也 接近。而后者的估计算法比较方便实用,因此应用更加普遍。

2.5 时间序列模型的定阶

实际上在进行时间虚列模型的参数估计之前首先要确定模型的阶数，该部分参数可以作为超参数通过优化得到，同时时间序列分析中有专门的模型定阶方法：

• 偏相关定阶法
• 白度检验定阶法
• F检验定阶法
• 准则函数定阶法
• 信息熵定阶法

2.6 时间序列模型残差的白噪声检验

由于ARMA模型的识别与估计是在假设随机扰动项为白噪声的基础上进行的。如果通过所估计的模型计算的样本残差不是白噪声，则索命模型的识别与估计有误，需要重新识别与估计。
得到白噪声序列，就说明时间序列中有用的信息已经被提取完毕了，剩下的全是随机扰动，是无法预测和使用的，残差序列如果通过了白噪声检验，则建模就可以终止了，因为没有信息可以继续提取。如果残差不是白噪声，就说明残差中还有有用的信息，需要修改模型或者进一步提取。
如果序列的所有观测值都是独立同分布的，而且他的均值μ和方差σ2都是有穷的常数，则该序列称为白噪声(white noise)或纯随机过程。可用QLB的统计量进行卡方检验来进行白噪声的检测。

3. 时间序列分解与谱估计

3.1 时间序列的季节调整、趋势分解与指数平滑

任何时间序列都可以认为由合理的函数变化后的三个部分（趋势部分、季节项部分和随机噪声部分）组成，时间序列各部分构成的基本模型为：

季节性波动会遮盖或混淆经济发展时间序列中的规律，进行时间序列的趋势分析时需要去掉季节波动的影响。将季节要素从原序列中剔除，这就是所谓的季节调整。
常用的季节调整方法（同时会剥离出季节项）有：

• X11方法
• Census X12方法
• 移动平均方法
• tramo/Seats方法

事件序列的趋势分解一般也包含循环要素。常用的测定长期趋势方法有：

• 回归分析方法
• 移动平均法
• 阶段平均法
• HP滤波方法
• 频谱滤波方法

指数平滑是可调整预测的简单方法，当只有少数观测值时这种方法是有效的，与使用固定系数的回归预测模型不同，指数平滑法的预测用过去的预测误差进行调整。常用的指数平滑方法有：

• 但指数平滑
• 双指数平滑
• Holt-Winters（无季节趋势、加法模型以及惩罚模型）

3.2 时间序列谱估计分析

对于样本功率谱的估计可以有两种不同的方法,其中一种是间接估计法,即先求样本自相 关,然后通过 FFT 变换来获得频率域上的样本功率谱。另外一种方法则是先求样本数据的瞬 时频率,然后在频率域上按定义计算其功率谱,故称为直接法。由于样本自相关比较容易得 到,因此通常采用间接法计算样本功率谱更为实际。

4 时间序列的分析汇总

项目	分析方法	Python工具	链接
平稳性检验	ADF检验	statsmodels.tsa.stattools.adfuller	http://www.statsmodels.org/devel/generated/statsmodels.tsa.stattools.adfuller.html?highlight=adfuller#statsmodels.tsa.stattools.adfuller
转化为平稳序列	差分	pandas.diff()	http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.diff.html
正态性检验	D’Agostino and Pearson’s test	scipy.stats.normaltest	https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.stats.normaltest.html
独立性检验	卡方检验	scipy.stats.chi2_contingency	https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html
季节项分解	移动平均	statsmodels.tsa.seasonal.seasonal_decompose	http://www.statsmodels.org/dev/generated/statsmodels.tsa.seasonal.seasonal_decompose.html?highlight=seasonal_decompose#statsmodels-tsa-seasonal-seasonal-decompose
模型选择与定阶	自相关系数与偏相关系数	statsmodels.tsa.stattools.acf（/pacf）	http://www.statsmodels.org/stable/generated/statsmodels.tsa.stattools.acf.html
参数估计	arma	statsmodels.tsa.arima_model.ARIMA	http://www.statsmodels.org/devel/generated/statsmodels.tsa.arima_model.ARIMA.html?highlight=statsmodels tsa arima_model