Opencv Python开发 第三章 图像检索
文章目录
- 章节简介
- 往期博客
- 特征的定义
- 特征检测算法
- 角点检测
- 什么是角点
- Harris角点检测
- 基本原理
- 代码实现
- 代码分析
- FAST角点检测
- 基本原理
- 代码实现
- 代码分析
- Harris和FAST角点检测的缺点
- 特征提取与描述
- SIFT特征提取
- 基本原理
- SIFT特性
- 代码实现
- 代码分析
- 验证尺度和旋转不变性
- 快速Hessian和SURF特征提取
- Hessian矩阵
- SURF基本原理
- 代码实现
- 基于ORB的特征检测和匹配
- ORB基本原理
- BRIEF
- BF暴力匹配
- 代码实现
- 代码分析
- KNN最近邻匹配
- 基本原理
- 代码实现
- FLANN匹配
- 代码实现
- 代码分析
- FLANN的单应性匹配
- 什么是单应性
- 代码实现
- 代码分析
- 章节总结
- 本章新的API
- 本章完整代码
章节简介
计算机不能像人眼一样, 可以非常直接地匹配出两张相似图像之间的特征点, 因此为了让计算机能够检测到图像的主要特征, 利用关键点将图像拼接起来, 我们需要对图像进行检索和特征匹配.
进一步的, 我们可以在已经提取出来的特征上, 抽象出一个特征类, 使其成为图像的描述符, 能够应用于所有图像的检索.
本章将介绍OpenCV如何进行图像特征匹配和检索, 重点是通过 单应性(homography) 来检测这些特征点是否和另一张图片相匹配
往期博客
PythonOpencv开发 Python3.6.7+Opencv3.4.2.16环境配置
PythonOpenCV开发 前言
OpenCV Python开发 第一章 图像处理基础
OpenCV Python开发 第一章课后 自定义实现API
OpenCV Python开发 第二章 深度估计与分割
特征的定义
粗略地讲, 特征就是图像中那些对于我们来说有意义的, 我们感兴趣关注的区域, 可以是一个像素点pixel, 也可以是一个超像素superpixel. 这些区域具有独特性并且易于人眼识别.
角点, 高密度区域, 以及高梯度区域(高梯度意味着附近像素值变化特别高)都是很好的特征. 比如我们能够从很多个大小不同的圆的图形中, 快速找到一个三角形, 却不一定能够找到一个被指定的圆.
而剩下来的大量的重复的模式, 或者低密度低梯度区域不是典型的特征, 因为他们变化太不明显, 一个典型的例子就是背景. 我们对一副图像进行检索, 很少是为了关注它的背景, 而不是它的内部的对象.
那么, 在图像中区分背景和对象的, 也就是边缘, 从上面的理解来看, 边缘也是非常好的特征. 事实上Harris角点检测的原理就用到了边缘的概念.
小结一下, 图像的特征就是指, 我们感兴趣的, 对我们有意义的图像的一小部分, 通常是指角点, 高密度区域, 高梯度区域, 或者是图像边缘.
特征检测算法
目前主流的特征检测算法有很多, 但是专注的方向不同, OpenCV中常见的用来提取特征的算法有:
- Harris, FAST: 角点检测
- SIFT, SURF, BRIEF: 斑点检测
- ORB: 带方向的FAST与旋转不变性的BRIEF
而用来进行特征匹配的有:
- 暴力(Brute-Force)法
- 基于FLANN(近似最邻近快速库, Fast Library for Approximate Nearest Neighbors)的匹配法
角点检测
什么是角点
我们人眼可以很明显地分辨出哪些属于角点, 比如树尖, 针头. 但是如何从数学角度去定义一个角点?
首先它要很小, 很尖, 这是生活中我们实际看到的角点的两个基本特征. 但是在图像中, 大小是没有多少参考意义的, 同样的图像, 我可以通过放大和缩小改变对象的大小. 即使图里是一根铁杵, 我也能将其缩小, 直到它变成一根针.
那么入手的角度就只剩下"尖"这一个关键词了. 万幸这不是一个实现起来特别复杂的概念. 我们理解的尖, 是指一个物体, 两个维度方向的长度完全不在一个量级. 比如针头, 它可以很长, 长到10厘米, 但是它的横截面积却连1平方毫米都不到.
因此我们可以这么定义角点: 该点处, 图像存在至少两个方向的梯度 f x , f y \Large f_x, f_y fx,fy, 两者绝对值相差特别大.
巧不巧? 刚好有一种算子, 可以计算水平和垂直方向上图像的梯度, 称为Sobel算子, 因此Sobel算子是用来检测角点的一个非常有用的工具. 下面分别是垂直和水平方向上的Sobel算子
[ − 1 − 2 − 1 0 0 0 1 2 1 ] [ − 1 0 1 − 2 0 2 − 1 0 1 ] \left[ \begin{matrix} \large \large -1 & \large -2 & \large -1 \\ \large 0 & \large 0 & \large 0 \\ \large 1 & \large 2 & \large 1 \end{matrix} \right] \left[ \begin{matrix} \large \large -1 & \large 0 & \large 1 \\ \large -2 & \large 0 & \large 2 \\ \large -1 & \large 0 & \large 1 \end{matrix} \right] ⎣⎡−101−202−101⎦⎤⎣⎡−1−2−1000121⎦⎤
Harris角点检测
基本原理
Harris角点检测的原理不算特别复杂, 这里提一下基本原理, 想深入理解的同学点击这里.
Harris从角点的定义出发, 利用一个窗口在图像上进行滑动, 过程中计算窗口内变化的梯度.
- 如果这个特定的窗口在图像各个方向上移动时,窗口内没有发生明显变化,那么窗口内就不存在角点.
- 如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段, 也就是对象的边缘.
- 如果在各个方向上移动这个特征的小窗口, 窗口内区域发生了较大的变化, 那么就认为在窗口内遇到了角点.
代码实现
def myHarris(img, showImg=True, space='bgr'):
"""
对img图像进行Harris角点检测
:param img: 输入图像, BGR三通道
:param showImg: 是否显示结果, 默认为是
:param space: 图像的色域空间
:return: Harris检测结果图像
:rtype: np.array
"""
img_orig = deepcopy(img)
img_copy = deepcopy(img)
if space not in ['gray', 'GRAY']:
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
else:
gray_img = deepcopy(img)
gray_img = np.float32(gray_img)
k1 = 0.04
harris_detector_k1 = cv.cornerHarris(gray_img, 2, 23, k1) # harris角点检测
dst_k1 = cv.dilate(harris_detector_k1, None) # 膨胀harris结果
thres_k1 = 0.01 * dst_k1.max() # 设置阈值
img[dst_k1 > thres_k1] = [0, 0, 255] # 检测出来的角点像素用红色标出
if showImg:
for i in range(2):
plt.subplot(1, 2, i + 1)
if 0 == i:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img_orig, cv.COLOR_BGR2RGB))
else:
plt.imshow(cv.cvtColor(img_orig, cv.COLOR_GRAY2RGB))
plt.title("原图")
elif 1 == i:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img, cv.COLOR_BGR2RGB))
else:
plt.imshow(cv.cvtColor(img, cv.COLOR_GRAY2RGB))
plt.title("Harris角点检测, k={}".format(k1))
plt.xticks([]), plt.yticks([]) # 隐藏X,Y轴
plt.show()
return img
运行结果如下:
代码分析
首先我们需要将输入图像img转化为灰度格式, 然后调用cornerHarris函数:
dst = cv.cornerHarris(img_gray, 2, 23, k)
这个函数原型如下:
cornerHarris(src, blockSize, ksize, k, dst=None, borderType=None)
其中重要的四个参数:
- src: 输入的图像, float32类型
- blockSize: 角点检测中要考虑的领域大小
- ksize: 求导中使用的窗口大小
- k: 角点检测方程中的自由参数,取值参数通常为[0,04,0.06]
最重要的是第三个参数ksize, 它限定了cornerHarris使用的Sobel算子的中孔(aperture), Sobel算子通过对图像的行, 列的变化来检测边缘. 简单地说, 这个参数定义了角点检测的敏感度, 取值通常为3和31之间的奇数.
下面这行实现了膨胀(dilate), 可以将前景物体放大.
dst_k1 = cv.dilate(harris_detector_k1, None)
函数原型如下:
dilate(src, kernel, dst=None, anchor=None, iterations=None, borderType=None, borderValue=None)
其中src为输入的灰度图像, kernel可以取None值, 也可以取以下的值:
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3)) # 椭圆结构
kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (3, 3)) # 十字结构
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3)) # 矩形结构
最后, 是对阈值的处理
img[dst_k1 > thres_k1] = [0, 0, 255] # 检测出来的角点像素用红色标出
注意这里的img为没有被转化过的BGR原始图像, 因此是三通道的. thres_k1为设置的阈值, dst_k1为膨胀处理过的输出图像, dst_k1 > thres_k1会返回一个bool型矩阵, 如果dst_k1对应的元素值大于thres_k1, 那么结果中对应的元素为True, 否则为False. 像下面这样
a = np.ones((4, 4))
a[1][2] = 0
print(a == 1)
"""
[[ True True True True]
[ True True False True]
[ True True True True]
[ True True True True]]
"""
之后, img[condition] = [0, 0, 255] 会将condition中, 值为true的对应位置的元素赋值为[0, 0, 255], 对应BGR中的红色
FAST角点检测
基本原理
FAST(Features from Accelerated Segment Test) 由Edward Rosten和Tom Drummond在2006年首先提出,是近年来一总倍受关注的基于模板和机器学习的角点检测方法,它不仅计算速度快,还具有较高的精确度。
该算法的原理是取图像中检测点,以该点为圆心的周围的16个像素点判断检测点是否为角点,通俗的讲就是中心的的像素值比大部分周围的像素值要亮一个阈值或者暗一个阈值则为角点.
具体的算法介绍点击这里
代码实现
def myFAST(img, showImg=True, space='bgr'):
"""
对img图像进行FAST角点检测
:param img: 输入图像, BGR三通道
:param showImg: 是否显示结果, 默认为是
:param space: 图像的色域空间
:return: FAST检测结果图像
:rtype: np.array
"""
fast = cv.FastFeatureDetector_create()
img_orig = deepcopy(img)
# 找到所有关键点
fast.setNonmaxSuppression(0)
kp = fast.detect(img, None)
img_colored = cv.drawKeypoints(img, kp, None, color=(0, 0, 255))
if showImg:
for i in range(2):
plt.subplot(1, 2, i + 1)
if 0 == i:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img_orig, cv.COLOR_BGR2RGB))
else:
plt.imshow(cv.cvtColor(img_orig, cv.COLOR_GRAY2RGB))
plt.title("原图")
elif 1 == i:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img_colored, cv.COLOR_BGR2RGB))
else:
plt.imshow(cv.cvtColor(img_colored, cv.COLOR_GRAY2RGB))
plt.title("FAST角点检测")
plt.xticks([]), plt.yticks([]) # 隐藏X,Y轴
plt.show()
return img_colored
运行结果如下:
FAST算法是一个非常不错的算法, 速度非常快, 但缺点也非常明显: 对噪音并不稳健. 容易把噪点误判为角点.
代码分析
这里用到了一个类对象fast = cv.FastFeatureDetector_create(), 详细的成员函数和变量请参考官方API文档
通常情况下, fast对象的一般用法为:
- 创建对象
fast = cv.FastFeatureDetector_create() - 非极大抑制
fast.setNonmaxSuppression(0) - 检测关键点
kp = fast.detect(img, None) - 将关键点标记在原图像上
img_colored = cv.drawKeypoints(img, kp, None, color=(0, 0, 255))
不光FAST对象是这样的流程, 后面介绍的SIFT, SURF, ORB, FLANN等对象都是这个逻辑和流程.
Harris和FAST角点检测的缺点
通常情况下, 前面介绍的Harris和FAST都可以很好的检测角点, 而且即使图像经过了旋转, 这两个算法仍然具有理想的效果.
但是, 如果队图像进行缩放处理(以缩小为例), 可能会检测到比原图更多的角点. 因此这两个算法对图像大小是及其敏感的(称为特征损失), 下图是一个示例
特征提取与描述
由于特征损失的存在, 我们就需要一种与图像比例无关的角点检测方法来解决. SIFT可以很好的解决这个问题.
SIFT特征提取
基本原理
SIFT(Scale-Invariant Feature Transform)有David Lowe于1999年提出的, 该算法会对不同的图像大小输出相同的结果(前提是遵循尺度不变特征变换). 需要注意的是, SIFT并不直接检测关键点, 但会通过一个特征向量来描述关键点周围区域的情况.
SIFT使用 DoG(Difference of Gaussians) 来检测关键点. DoG是对同一图像使用不同高斯滤波器所得到的结果. SIFT对象会使用DoG来检测关键点, 并且对每个关键点周围的取余计算特征向量. 返回值是关键点信息和描述符, 同上文的fast对象一样, 需要我们手动把这些描述符标注到原图像上.
SIFT特性
- 对旋转、尺度缩放、亮度变化等保持不变性
- 对视角变换、仿射变化、噪声也保持一定程度的稳定性
- 独特性好,信息量丰富,适用于海量特征库进行快速、准确的匹配;
- 多量性,即使是很少几个物体也可以产生大量的SIFT特征;
- 高速性,经优化的SIFT匹配算法甚至可以达到实时性的要求;
- 扩展性,可以很方便的与其他的特征向量进行联合
代码实现
def mySIFTSURF(img, showImg=True, space='bgr', select='sift', thres=None):
"""
对输入图像img做SIFT或者SURF处理
:param img: 输入图像
:param showImg: 是否显示结果, 默认为是
:param space: 图像色域空间
:param select: 选择SIFT还是SURF
:param thres: SURF的阈值
:return: 处理后的图像, 关键点, 以及描述符
:rtype: np.array, np.array, np.array
"""
height, width = img.shape[:2]
small_size = 0.6
img_orig = deepcopy(img) # 原图
if select in ['sift', 'SIFT']:
algo = cv.xfeatures2d.SIFT_create()
else:
algo = cv.xfeatures2d.SURF_create(thres)
if space in ['bgr', 'BGR']:
kp, descri = algo.detectAndCompute(cv.cvtColor(img, cv.COLOR_BGR2GRAY), None)
else:
kp, descri = algo.detectAndCompute(img, None)
img_processed = cv.drawKeypoints(deepcopy(img), outImage=img, keypoints=kp,
flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
if showImg:
ttls = ['原图', '原图{}'.format(select)]
imgs = [img_orig, img_processed]
for i in range(2):
plt.subplot(1, 2, i + 1)
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(imgs[i], cv.COLOR_BGR2RGB))
else:
plt.imshow(imgs[i])
plt.title(ttls[i])
plt.xticks([]), plt.yticks([]) # 隐藏X,Y轴
plt.show()
return img_processed, kp, descri
运行结果如下, SIFT会以关键点为圆心, 画一个圆, 并指出特征向量的方向.
下面是局部的图像
代码分析
和前文的FAST算法是一样的流程, 只不过创建的类不同罢了, 函数参数上也有一些小的变动.
这里我们先是创建了一个SIFT对象 sift = cv.xfeatures2d.SIFT_create(), 然后计算关键点 kp, descri= sift.detectAndCompute(img, None), 最后再在原图上标出这些关键点 img_sift = cv.drawKeypoints(image=deepcopy(img), outImage=img, keypoints=kp, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
上面的 flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS 其实可以用 flags=4来代替
另外稍微提一下, 关键点既然包含了坐标和方向两个属性, 那么很容易想到它应该是一个对象类, 而不是基本数据类型.
事实上, 从官方的文档会发现, 关键点keypoint类有以下成员变量
- pt: 表示图像中关键点的x,y坐标
- size: 特征的直径
- angle: 特征的方向
- response: 关键点的强度. 某些特征会通过SIFT来分类, 因为他得到的特征比其它特征更好, 通过查看response属性可以品谷特征强度
- octave: 表示特征所在金字塔的层级. SIFT算法用到了高斯金字塔.
验证尺度和旋转不变性
前文提到过, SIFT具有尺度和旋转的不变形, 下面我们来写两个demo验证一下.
我们创建一个0.6倍率缩小的原图的副本, 进行同样的SIFT操作, 然后将两者拼接起来, 相匹配的关键点我们用线连接起来
同理我们再创建一个逆时针旋转45度的副本, 进行同样的操作.
首先我们定义一个旋转图片的函数 rotateImage(img, angle, resize=1.0), 由于直接使用opencv的API会导致旋转后的图片缺少一块, 所以我们要自定义一个函数. 实现将旋转后的图片的大小重新调整, 使得整张图片得到保存.
def rotateImage(img, angle, resize=1.0):
"""
将img逆时针旋转angle角度
:param img: 输入图像
:param angle: 逆时针旋转角度
:param resize: 缩放大小
:return: 旋转后的图像
:rtype: np.array
"""
(h, w) = img.shape[:2]
(cX, cY) = (w // 2, h // 2)
M = cv.getRotationMatrix2D((cX, cY), angle, resize)
cos = np.abs(M[0, 0])
sin = np.abs(M[0, 1])
nW = int((h * sin) + (w * cos))
nH = int((h * cos) + (w * sin))
M[0, 2] += (nW / 2) - cX
M[1, 2] += (nH / 2) - cY
img_rotated = cv.warpAffine(img, M, (nW, nH))
return img_rotated
接着我们定义一个用FLANN进行特征匹配的函数, FLANN具体会在后面介绍, 这里只是先调用一下.
def FlannMatch(img1, img2, ttl='FLANN匹配', showImg=True, space='bgr'):
"""
将im1和img2进行flann匹配
:param img1: 输入图像1
:param img2: 输入图像2
:param ttl: 最终显示图片的名称
:param showImg: 是否显示匹配结果, 默认为是
:param space: img1和img2的色域空间
:return: 匹配结果图像, 匹配的关键点
:rtype: np.array, list
"""
sift = cv.xfeatures2d.SIFT_create()
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, tree=5)
searchparams = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, searchparams)
cv.FlannBasedMatcher_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
matches = flann.knnMatch(des1, des2, k=2)
good = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good.append([m])
img5 = cv.drawMatchesKnn(img1, kp1, img2, kp2, good, None, flags=2)
if showImg:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img5, cv.COLOR_BGR2RGB))
else:
plt.imshow(img5)
plt.xticks([]), plt.yticks([])
plt.title(ttl)
plt.show()
return img5, good
最后我们定义一个验证SIFT尺度和旋转不变性的函数
def checkSIFT(img, space='bgr'):
"""
检查SIFT的尺度和旋转不变性
:param img: 输入图像
:param space: 图像的色域空间
"""
height, width = img.shape[:2]
small_size = 0.6
img_orig = deepcopy(img)
img_small = cv.resize(deepcopy(img), (int(small_size * width), int(small_size * height)),
interpolation=cv.INTER_CUBIC)
img_rotate = rotateImage(deepcopy(img), 45)
FlannMatch(deepcopy(img_orig), deepcopy(img_small), ttl='尺度不变性验证')
FlannMatch(deepcopy(img_orig), deepcopy(img_rotate), ttl='旋转不变性验证')
return
运行checkSIFT()结果如下
可以看到, 两张图片中的每个关键点都有对应的关键点进行匹配. 这就是SIFT的尺度和旋转不变性.
快速Hessian和SURF特征提取
与SIFT相比, SURF(Speeded Up Robust Features) 是一种更快速的算法, 由Herbert Bay于2006年提出, 吸收了SIFT的思想, 但是速度上比SIFT快好几倍
Hessian矩阵
黑塞矩阵(Hessian Matrix) 是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。
说白了, 就是多元函数的泰勒展开式需要用到Hessian矩阵, 除此之外, Hessian矩阵还涉及到很多数学相关的知识点,比如极值判断、矩阵特征值及特征向量、二次型等
具体的介绍请点击这里
SURF基本原理
SURF与SIFT构造的金字塔有很大不同, 也正是因此, SURF比SIFT快得多. SIFT采用的是DoG图像,而SURF采用的是Hessian矩阵行列式近似值图像。以下是图像中某个像素点的Hessian矩阵:
H ( x , σ ) = [ L x x ( x , σ ) L x y ( x , σ ) L x y ( x , σ ) L y y ( x , σ ) ] \large H(x, \sigma) = \left[ \begin{matrix} \large \large L_{xx}(x, \sigma) & \large L_{xy}(x, \sigma) \\ \large L_{xy}(x, \sigma) & \large L_{yy}(x, \sigma) \end{matrix} \right] H(x,σ)=[Lxx(x,σ)Lxy(x,σ)Lxy(x,σ)Lyy(x,σ)]
其中 L x x ( x , σ ) \large L_{xx}(x, \sigma) Lxx(x,σ) 是是高斯二阶微分在像素点(x, y)处与图像函数 I ( x , y ) \large I(x,y) I(x,y) 的卷积
此外, SURF还用到了一个图像积分的概念. 所谓的图像积分, 对于像素点(x, y)的积分 S ( x , y ) \large S(x,y) S(x,y), 其值等于所有位于该像素点左上角的所有像素的和. 写成公式如下:
S ( x , y ) = ∑ i = 0 x ∑ j = 0 y I ( i , j ) \large S(x, y) = \sum_{i=0}^x \sum_{j=0}^y I(i, j) S(x,y)=i=0∑xj=0∑yI(i,j)
代码实现
SURF的代码与SIFT的事实上只有一行不同, 就是创建的对象不同. 因此我们完全可以改一下SIFT的代码, 没必要再写一个函数
def mySIFTSURF(img, showImg=True, space='bgr', select='sift', thres=None):
"""
对输入图像img做SIFT或者SURF处理
:param img: 输入图像
:param showImg: 是否显示结果, 默认为是
:param space: 图像色域空间
:param select: 选择SIFT还是SURF
:param thres: SURF的阈值
:return: 处理后的图像, 关键点, 以及描述符
:rtype: np.array, np.array, np.array
"""
height, width = img.shape[:2]
small_size = 0.6
img_orig = deepcopy(img) # 原图
if select in ['sift', 'SIFT']:
algo = cv.xfeatures2d.SIFT_create()
else:
algo = cv.xfeatures2d.SURF_create(thres)
if space in ['bgr', 'BGR']:
kp, descri = algo.detectAndCompute(cv.cvtColor(img, cv.COLOR_BGR2GRAY), None)
else:
kp, descri = algo.detectAndCompute(img, None)
img_processed = cv.drawKeypoints(deepcopy(img), outImage=img, keypoints=kp,
flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
if showImg:
ttls = ['原图', '原图{}'.format(select)]
imgs = [img_orig, img_processed]
for i in range(2):
plt.subplot(1, 2, i + 1)
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(imgs[i], cv.COLOR_BGR2RGB))
else:
plt.imshow(imgs[i])
plt.title(ttls[i])
plt.xticks([]), plt.yticks([]) # 隐藏X,Y轴
plt.show()
return img_processed, kp, descri
运行结果如下
基于ORB的特征检测和匹配
ORB(Oriented Fast and Rotated BRIEF) 算法是基于FAST特征检测与BRIEF特征描述子匹配实现,相比BRIEF算法中依靠随机方式获取而值点对,ORB通过FAST方法,FAST方式寻找候选特征点方式是假设灰度图像像素点A周围的像素存在连续大于或者小于A的灰度值. 与SIFT和SURF相比, ORB的速度更快.
在ORB的论文中, 作者得到了如下的成果:
- 向FAST增加一个快速,准确的方向分量(component)
- 高效计算带方向的BRIEF特征
- 基于带方向的BRIEF特征的方差分析和相关分析
- 在旋转不变性条件下学习一种不相关的BRIEF特征, 使得算法在KNN的应用中得到较好的性能.
ORB旨在优化和加快速度, 包括以 旋转感知(rotate-aware) 的方式使用BRIEF, 这样即使在训练图像与查询图像之间旋转差别很大的情况下也能够提高匹配效果.
ORB基本原理
BRIEF
ORB是基于FAST和BRIEF算法的, FAST已经在前文介绍过了, 这里简单介绍一下BRIEF.
BRIEF是2010年的一篇名为《BRIEF: Binary Robust Independent Elementary Features》的文章中提出,BRIEF是对已检测到的特征点进行描述,它是一种二进制编码的描述子,摈弃了利用区域灰度直方图描述特征点的传统方法,大大的加快了特征描述符建立的速度,同时也极大的降低了特征匹配的时间,是一种非常快速,很有潜力的算法。
由于BRIEF仅仅是特征描述子,所以事先要得到特征点的位置,可以利用FAST, Harris, SIFT, SURF等算法检测特征点的位置。接下来在特征点邻域利用BRIEF算法建立特征描述符。
BRIEF是目前最快的特征描述符, 相应地理论也非常复杂.
BF暴力匹配
暴力匹配(Brute-Force) 是一种描述符匹配方法, 该方法会比较两个描述符, 并产生匹配结果的列表list. 称为暴力匹配的原因是该算法不进行任何优化, 两个描述符集一一进行比较. 每次比较两个描述符.
OpenCV提供了BFMatcher对象来实现暴力匹配.
代码实现
我们选取两张尽可能相似的图片, 比如不同时间点, 同一景点的照片, 这样建筑整体是相似的, 人群是唯一的不确定因素.
这里我选取以下两张故宫的照片.
def myORB(img1, img2, showImage=True, select='ORB', k=None):
"""
对img1和img2进行ORB或者KNN匹配
:param img1: 输入图像1, grayscale类型
:param img2: 输入图像2, grayscale类型
:param showImage: 是否显示结果, 默认为是
:param select: 选择暴力BF还是KNN匹配
:param k: KNN匹配的k
:return: 匹配的结果和匹配的关键点
:rtype: np.array, list
"""
orb = cv.ORB_create()
kp1, des1 = orb.detectAndCompute(deepcopy(img1), None)
kp2, des2 = orb.detectAndCompute(deepcopy(img2), None)
bf = cv.BFMatcher_create(cv.NORM_HAMMING, crossCheck=True)
if select in ['orb', 'ORB']:
matches = bf.match(des1, des2)
matched = sorted(matches, key=lambda x: x.distance)
img3 = cv.drawMatches(img1, kp1, img2, kp2, matches, None, flags=2)
else:
matches = bf.knnMatch(des1, des2, k=k)
img3 = cv.drawMatchesKnn(img1, kp1, img2, kp2, matches, None, flags=2)
if showImage:
plt.imshow(cv.cvtColor(img3, cv.COLOR_BGR2RGB))
plt.xticks([]), plt.yticks([])
plt.title('ORB+{}匹配'.format(select))
plt.show()
return img3, matches
运行结果如下, 可以看到效果不是特别理想.
代码分析
直到 kp2, des2 = orb.detectAndCompute(img2, None), 都和前面SIFT, SURF的逻辑是一样的.
接下来我们接触到了第一个匹配类型的对象BFMatcher
bf = cv.BFMatcher_create(cv.NORM_HAMMING, crossCheck=True)
这行行我们创建类BFMatcher对象, 函数原型为:
def BFMatcher_create(normType=None, crossCheck=None)
参数说明:
- normType:用来指定要使用的距离测试类型。默认值为cv2.Norm_L2。这很适合SIFT和SURF等. 对于使用二进制描述符的ORB、BRIEF和BRISK算法等,要使用cv2.NORM_HAMMING,这样就会返回两个测试对象之间的汉明距离. 如果ORB算法的参数设置为WTA_K==3或4,normType就应该设置成cv2.NORM_HAMMING2.
- crossCheck:针对暴力匹配, 可以使用交叉匹配的方法来过滤错误的匹配. 默认值为False. 如果设置为True, 匹配条件就会更加严格,只有到A中的第i个特征点与B中的第j个特征点距离最近,并且B中的第j个特征点到A中的第i个特征点也是最近时才会返回最佳匹配(i, j),即这两个特征点要互相匹配才行。
这句其实可以用 bf = cv.BFMatche(cv.NORM_HAMMING, crossCheck=True)代替, 两者的效果是一样的.
接着我们对计算出来的描述符进行匹配:
matches = bf.match(des1, des2)
matches = sorted(matches, key=lambda x:x.distance)
BFMatcher对象其实有两个匹配算法, 一个是 bf.match(des1, des2), 另一个是 bf.knnMatch(des1, des2), 两者的区别想必看名字就知道了, 前者返回最佳匹配, 对一个匹配目标只返回一个最佳的匹配结果. 而后者通过KNN算法, 返回k个最佳匹配.
之后由于暴力匹配复杂度实在太高, 我们先对匹配出来的结果按照距离进行排序, 再标注到原图上:
img3 = cv.drawMatches(img1, kp1, img2, kp2, matches, None, flags=2)
cv.drawMatches() 函数之前的函数 cv.drawKeypoints() 特别像, 容易搞混. 前者是将两张图像上匹配的关键点连线标出, 后者是在单张图像上绘制出关键点.
KNN最近邻匹配
熟悉机器学习, 特别是sklearn库的同学可能对KNN这个算法很了解.
KNN(K-Nearest Neighbors)可能是机器学习中最简单的分类算法之一了, 背后的理论也很简单.
基本原理
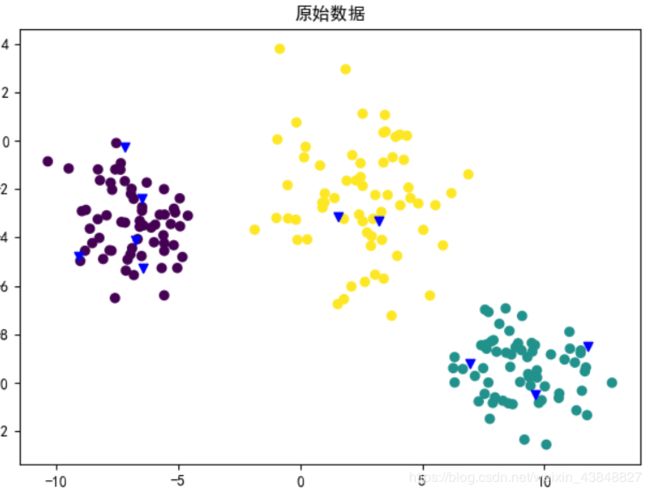
以二维平面上的不同点集为例. 假设有以下三个经过分类的圆形点集(紫, 黄, 青), 给定几个样本(蓝色三角标出), 要求分别给这几个样本进行分类.
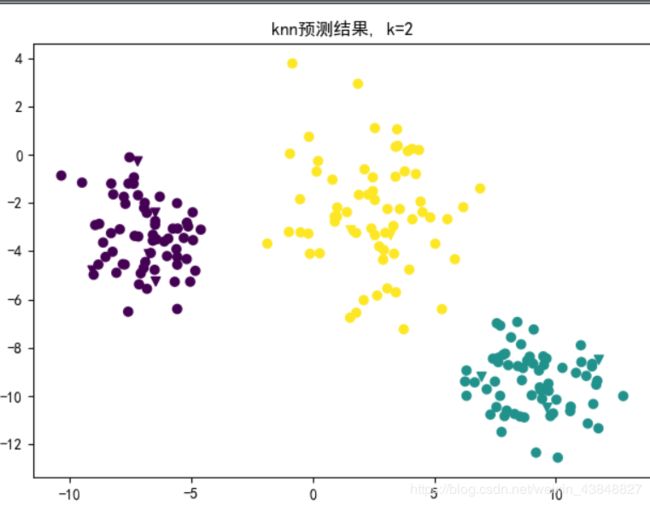
KNN的思想是, 对于每个样本, 分别计算其与已知类别的距离(本例中是欧氏距离), 然后选择最小的K个结果返回.
以下是结果, 可以看到所有原本是蓝色的三角都被很好地分到了对应的类中.
代码实现
前面ORB中提到过, BFMatcher对象提供了暴力匹配 bf.match() 和KNN匹配 bf.knnMatch() 两个算法, 因此只需改动一下代码就好了. 注意KNN匹配的结果无需再另外排序
def myORB(img1, img2, showImage=True, select='ORB', k=None):
"""
对img1和img2进行ORB或者KNN匹配
:param img1: 输入图像1, grayscale类型
:param img2: 输入图像2, grayscale类型
:param showImage: 是否显示结果, 默认为是
:param select: 选择暴力BF还是KNN匹配
:param k: KNN匹配的k
:return: 匹配的结果和匹配的关键点
:rtype: np.array, list
"""
orb = cv.ORB_create()
kp1, des1 = orb.detectAndCompute(deepcopy(img1), None)
kp2, des2 = orb.detectAndCompute(deepcopy(img2), None)
bf = cv.BFMatcher_create(cv.NORM_HAMMING, crossCheck=True)
if select in ['orb', 'ORB']:
matches = bf.match(des1, des2)
matched = sorted(matches, key=lambda x: x.distance)
img3 = cv.drawMatches(img1, kp1, img2, kp2, matches, None, flags=2)
else:
matches = bf.knnMatch(des1, des2, k=k)
img3 = cv.drawMatchesKnn(img1, kp1, img2, kp2, matches, None, flags=2)
if showImage:
plt.imshow(cv.cvtColor(img3, cv.COLOR_BGR2RGB))
plt.xticks([]), plt.yticks([])
plt.title('ORB+{}匹配'.format(select))
plt.show()
return img3, matches
运行结果如下:
FLANN匹配
最后, 介绍FLANN匹配.
FLANN(Fast Library for Approximate Nearest Neighbors), 从命名可以看出, FLANN求得的是近似的最近邻, 因此条件比SIFT, SURF以及KNN宽松很多, 相应的结果也就不会特别准确. 牺牲准确度以换取速度.
FLANN网站有一段话:
FLANN is a library for performing fast approximate nearest neighbor searches in high dimensional spaces. It contains a collection of algorithms we found to work best for nearest neighbor search and a system for automatically choosing the best algorithm and optimum parameters depending on the dataset.
FLANN is written in C++ and contains bindings for the following languages: C, MATLAB, and Python.
简单地说, 就是FLANN具有一种内部机制, 能够自动根据传递的参数, 选择最合适的算法来处理数据. FLANN处理的速度是其它最近邻软件的几倍以上.
需要注意的是, FLANN并不是一个算法, 它是一个库(命名中有Library), FLANN使用的还是其它的算法. 只是很好地将其他算法封装成了一个抽象类.
代码实现
前面已经定义过FLANN匹配的函数了, 这里再复制一遍
def FlannMatch(img1, img2, ttl='FLANN匹配', showImg=True, space='bgr'):
"""
将im1和img2进行flann匹配
:param img1: 输入图像1
:param img2: 输入图像2
:param ttl: 最终显示图片的名称
:param showImg: 是否显示匹配结果, 默认为是
:param space: img1和img2的色域空间
:return: 匹配结果图像, 匹配的关键点
:rtype: np.array, list
"""
sift = cv.xfeatures2d.SIFT_create()
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, tree=5)
searchparams = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, searchparams)
cv.FlannBasedMatcher_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
matches = flann.knnMatch(des1, des2, k=2)
good = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good.append([m])
img5 = cv.drawMatchesKnn(img1, kp1, img2, kp2, good, None, flags=2)
if showImg:
if space in ['bgr', 'BGR']:
plt.imshow(cv.cvtColor(img5, cv.COLOR_BGR2RGB))
else:
plt.imshow(img5)
plt.xticks([]), plt.yticks([])
plt.title(ttl)
plt.show()
return img5, good
运行结果在前面验证SIFT尺度不变性的时候调用过了, 这里重复贴一下
代码分析
整体上FLANN的流程和逻辑和ORB还是相似的, 先创建对象
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, tree=5)
searchparams = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, searchparams)
然后将两张图像的描述符进行匹配
matches = flann.knnMatch(des1, des2, k=2)
good = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good.append([m])
最后将匹配结果在原图上标出
img5 = cv.drawMatchesKnn(img1, kp1, img2, kp2, good, None, flags=2)
不过, FLANN对象在创建的时候有点不同. 可以看到最上面三行都是创建FLANN对象时用到的参数.
FlannBasedMatcher()原型如下:
class FlannBasedMatcher(__cv2.DescriptorMatcher):
def create(self): # real signature unknown; restored from __doc__
"""
create() -> retval
"""
pass
def __init__(self, *args, **kwargs): # real signature unknown
pass
@staticmethod # known case of __new__
def __new__(*args, **kwargs): # real signature unknown
""" Create and return a new object. See help(type) for accurate signature. """
pass
def __repr__(self, *args, **kwargs): # real signature unknown
""" Return repr(self). """
pass
FlannBasedMatcher()在调用时接收多个参数, 从__init__()中的 *args 和 **kwargs可以看出. 上面给出的参数都是dict字典类型的, 如下所示
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, tree=5)
searchparams = dict(checks=50)
print(index_params, searchparams)
"""
{'algorithm': 0, 'tree': 5} {'checks': 50}
"""
而熟悉python的同学应该知道, 用字典传递的参数, 只能是**kwargs中的参数. 出于好奇, 我查了相关的资料, 想弄清楚这个__init__() 到底接收多少参数, 但是可以查到的资料几乎没有说明参数的. 这个坑留给以后填吧…
FLANN的单应性匹配
什么是单应性
A relation between two figures, such that to any point of the one corresponds one and but one point in the other, and vise versa. Thus, a tangent line rolling on a circle cuts two fixed tangents of the circle in two sets of points that are homographic.
翻译过来就是说, 单应性是这么一种条件, 该条件表明当两幅图像中的一副出现投影畸变(perspective distortion) 时, 他们还能彼此匹配.
所谓的投影畸变, 就是指视觉上的投影. 比如我们从侧面看一个正方形的时候, 看到的是一个斜着的长方形.
代码实现
首先我们要明确, 单应性匹配的输入和输出是什么.
- 输入: 两幅图像, 一副正视图, 一副侧视图
- 输出: 输入图像的匹配结果.
首先我们需要定义一个对图像进行投影运算的函数:
def perspectImage(img):
"""
将输入图像投影后返回
:param img: 输入图像
:return: 投影后的图像
:rtype: np.array
"""
h, w = img.shape[:2]
src = np.array([[0, 0], [w - 1, 0], [0, h - 1], [w - 1, h - 1]], np.float32)
dst = np.array([[50, 50], [w / 3, 50], [50, h - 1], [w - 1, h - 1]], np.float32)
P = cv.getPerspectiveTransform(src, dst) # 计算投影矩阵
r = cv.warpPerspective(img, P, (w, h), borderValue=125)
return r
效果如下:
接着, 我们定义函数来验证FLANN的单应性:
def checkFLANN(img):
"""
对FLANN进行单应性验证
:param img: 输入图像
"""
MIN_MATCH_COUNT = 15 # 小于这个数量则认为两张图像不是同一个对象
img1 = deepcopy(img)
img2 = perspectImage(img)
# 创建SIFT对象
sift = cv.xfeatures2d.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# 创建FLANN对象
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2) # 进行描述符匹配
# 保存有效的匹配点
good = []
for m, n in matches:
if m.distance < 0.7*n.distance:
good.append(m) # 注意这里不是good.append([m])
if len(good) < MIN_MATCH_COUNT:
print("Not enough matches are found, {} detected while {} required".
format(len(good), MIN_MATCH_COUNT))
return
src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1, 1, 2)
dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1, 1, 2)
M, mask = cv.findHomography(src_pts, dst_pts, cv.RANSAC, 5.0)
matchesMask = mask.ravel().tolist()
h, w = img.shape[:2]
pts = np.float32([ [0,0], [0,h-1], [w-1,h-1], [w-1,0] ]).reshape(-1, 1, 2)
dst = cv.perspectiveTransform(pts, M)
img2 = cv.polylines(img2, [np.int32(dst)], True, 255, 3, cv.LINE_AA)
draw_params = dict(matchColor=(0,255,255), singlePointColor=None,
matchesMask=matchesMask, flags=2)
img3 = cv.drawMatches(img1, kp1, img2, kp2, good, None, **draw_params)
plt.imshow(cv.cvtColor(img3, cv.COLOR_BGR2RGB))
plt.xticks([]), plt.yticks([])
plt.show()
运行结果如下:
代码分析
前半部分有一个小细节, 就是 good.append(m), 之前我们都是 good.append([m]), 这里我们用前者, 因为我们需要的是一个一维的描述符列表, 而不是二维的. 之前都是二维的.
直到if len(good) < MIN_MATCH_COUNT前, 都是我们非常熟悉的模式.
从这开始, 就是新内容了, 记下来, 很重要!
首先, 我们需要确保图像中至少有一定数目的点是匹配的, 不能说两张毫不相干的图像强行进行匹配. 这里我们设置这个数值为15. 当匹配的描述符数量小于15时, 认为这两张图片不是同一个对象. 直接退出函数.
接着, 我们来看下面这两句.
src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1, 1, 2)
dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1, 1, 2)
乍一看这写的啥啊, 又是kp又是pt的, 查了网上也没有太好的详解.
碰到这种查不到的问题怎么办?
根据上下文情景, 再结合变量和函数的命名, 以及自身的知识储备和直觉, 大胆地猜!
首先m.queryIdx中有Id的字眼, 而Id是用来唯一标识一个对象的, 再加上query查询的字样? 还不明显嘛? 我们就理解为通过一个id来查找对应的描述符m(有点类似超像素的id). 那么很容易联想到 kp1[m.queryIdx] 的作用就是根据 m.queryIdx返回的这个id, 在kp1列表中找到相应位置的keypoint关键点. 那么再联想一下, 关键点有什么属性? 至少得有坐标这个属性吧? 再结合后面np.reshape(-1, 1, 2)可知最后的结果是一个n行2列的二维矩阵, 类似下面这样
[[1, 1], [2, 2], [3, 3]]
这不就是坐标构成的列表嘛? 再说了, 我前面可是明确告诉你关键点kp有哪些成员变量的…其中第一个就是坐标pt… 忘了的往前翻…
至于a = [func(x) for x in list] 这种写法是Python中很常见的了. 就是对list中的每个元素作为参数传递给函数func(), 将结果保存在列表a中.
因此这两句的含义就很明显了: 分别查询原始图像和训练图像中发现的关键点的坐标, 并保存到列表src_pts和dst_pts中.
接着, 我们通过cv.findHomography()计算多个二维点对之间的最优单映射变换矩阵 H(3行3列), 使用最小均方误差或者RANSAC方法
该函数原型如下:
def findHomography(srcPoints, dstPoints, method=None, ransacReprojThreshold=None,
mask=None, maxIters=None, confidence=None)
参数说明:
- srcPoints: 源平面中点的坐标矩阵,可以是CV_32FC2类型,也可以是list类型
- dstPoints: 目标平面中点的坐标矩阵,可以是CV_32FC2类型,也可以是list类型
- method: 计算单应矩阵所使用的方法。不同的方法对应不同的参数,具体如下:
-
- 0 - 利用所有点的常规方法
- RANSAC - RANSAC-基于RANSAC的鲁棒算法
- LMEDS - 最小中值鲁棒算法
- RHO - PROSAC-基于PROSAC的鲁棒算法
- ransacReprojThreshold: 将点对视为内点的最大允许重投影错误阈值(仅用于RANSAC和RHO方法)
- mask: 可选输出掩码矩阵,通常由鲁棒算法(RANSAC或LMEDS)设置。 请注意,输入掩码矩阵是不需要设置的。
- maxIters: RANSAC算法的最大迭代次数,默认值为2000。
- confidence: 可信度值,取值范围为0到1.
而matchesMask = mask.ravel().tolsit(), 则是得到一个matchesMask, 最后用来绘制匹配图.
然后, 我们需要对第二张投影过的图计算相对于原始图像的投影畸变
h, w = img.shape[:2]
pts = np.float32([ [0,0], [0,h-1], [w-1,h-1], [w-1,0] ]).reshape(-1, 1, 2)
dst = cv.perspectiveTransform(pts, M)
img2 = cv.polylines(img2, [np.int32(dst)], True, 255, 3, cv.LINE_AA)
第一行之所以写成h, w = img.shape[:2], 而不写成h, w = img.shape的原因是, 如果img是三通道图像, 那么第二种写法会报错. 第一种写法默认只返回img.shape元组中的前两个参数, 也就是图像的高度和宽度.
最后的绘图过程于之前的例子是一样的. 不再赘述.
章节总结
本章介绍了如何检测图像特征以及如何为描述符提取特征, 探讨了如何通过OpenCV提供的API完成这个任务.
下一章将在本章的基础上, 介绍 级联(cascade) 的概念和自定义特征模型.
本章新的API
"""
OpenCV
"""
cv.getPerspectiveTransform(src, dst) # 计算投影矩阵
cv.warpPerspective(img, P, (w, h), borderValue=125) # 进行仿射投影
cv.getRotationMatrix2D((cX, cY), angle, resize) # 计算旋转矩阵
cv.warpAffine(img, M, (nW, nH)) # 进行图像旋转
cv.cornerHarris(gray_img, 2, 23, k1) # harris角点检测
cv.dilate(harris_detector_k1, None) # 膨胀操作
# 创建对象
cv.FastFeatureDetector_create()
cv.xfeatures2d.SIFT_create()
cv.xfeatures2d.SURF_create(thres)
cv.FlannBasedMatcher(index_params, searchparams)
kp, des = object.detectAndCompute(img, None) # 检测并计算关键点和描述符, object可以是SIFT, SURF等
cv.drawKeypoints(img, kp, None, color=(0, 0, 255)) # 标出关键点
本章完整代码
已上传至个人资源, 审核通过后, 点击此处 即可下载, (我也不知道怎么回事…提交的时候是无需积分的, 但是过段时间就变成需要2积分或者5积分了)