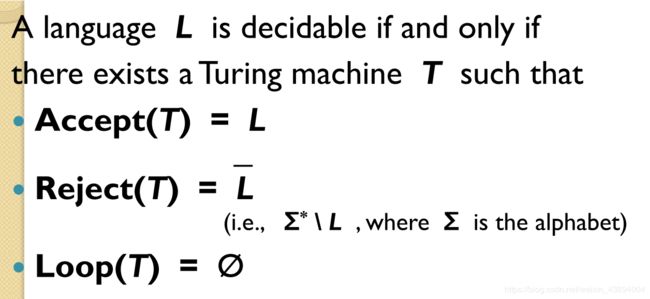Theory of computation 学习笔记(Monash FIT2014)
Theory of computation 学习笔记(Monash FIT2014)
- 声明
- Conjunctive Normal Form
- predicate logic
- induction
- Regular expression
- Automata
- Finite Automaton (FA)
- Nondeterministic Finite Automata (NFA)
- Kleene’s Theorem
- 互相转换
- Regular->NFA
- NFA->FA
- GNFA->regular
- 简化FA
- 正则语言的闭合性
- context free
- Context free -> PushDown
- NFA->CFG
- Chomsky Normal Form
- Cocke-Younger-Kasami (CYK) algorithm
- Church-Turing Thesis
- Decidable
- Recursively enumerable languages
声明
笔记内容来源于 monash university FIT2014 课程内容
仅供学习交流
Conjunctive Normal Form
在布尔逻辑中,如果一个公式是子句的合取,那么它是合取范式(CNF)的。
即,多个表达式的交集(∩)。
例: (B ∨ C ∨ T) ∧ (¬B ∨ ¬C) ∧ (¬B ∨ ¬T) ∧ (¬C ∨ ¬T)
predicate logic
In mathematical logic, a predicate is commonly understood to be a Boolean-valued function .
P: X→ {true, false}, called the predicate on X.
例:∀X : computer(X) ⇐⇒ automatic(X) ∧ programmable(X) ∧ storedProgram(X) ∧ generalPurpose(X)
这句表达式的意义为:对于任意计算机, 当且仅当它同时满足,是自动机,可被运行,可存储运行,能运算所有可计算问题,它被称为计算机。
induction
数学归纳法
证明步骤:
(i) Inductive basis:
(ii) Our inductive hypothesis is that …… is true for n. We need to use this to show that n can be replaced by n + 1 in this inequality
So, we’ve shown that, if the claimed inequality holds for n, then it holds for n + 1
(iii) By the Principle of Mathematical Induction, the claimed inequality must hold for all n.
即:
- 先列出base case, 例如对于n>=1的问题, n=1就是base case。
- 假设n=k时,成立
用1和2证明k+1时仍成立 - 得出结论,原式正确。
Regular expression
证明一个语言不是正则:
Pumping Lemma :
Then for all words w in L with more than N letters,
there exist strings x, y, z, with y ≠ ε, such that
◦ w = xyz
◦ length(x) + length(y) £ N
◦ for all i ≥ 0, xyiz is in L.
例:(证明语言DOG非正则)
Assume, by way of contradition, that DOG is regular. Then there is a FA that recognises it. Let N be the number of states in such an FA. Let w be the string grN (woof) N . By the Pumping Lemma, w can be divided up into three parts, w = xyz, such that y is nonempty, |xy| ≤ N, and xyi z ∈ DOG for all i ≥ 0. The requirement that |xy| ≤ N forces y to fall within the first part, grN , of w. Consider the string xyyz. If y contains g, then xyyz has two gs, so xyyz 6∈ DOG, since every string in DOG has exactly one g. If y contains no g, then it’s all-r, so repetition of y creates at least one extra r (since y is nonempty), so the number of rs is greater than the number of woofs, which violates the definition of DOG. So xyyz 6∈ DOG, which contradicts the conclusion of the Pumping Lemma. So our initial assumption, that DOG is regular, must be incorrect. So DOG is not regular.
Automata
自动机原理讲解见:
Finite Automaton (FA)
Every string traces a unique path in the automaton
即:对于每个state(点),需要分配所有输入类型的输出。比如:a,b 进入state3,那么state3一定有a和b的指出。
解题技巧:对于复杂情况,简化成该问题的反面,取补集。
accept->not accept and not accept-> accept
一个FA的反面:讲所有final改成nonfinal,nonfinal改为final。
Nondeterministic Finite Automata (NFA)
Kleene’s Theorem
Regular expression, FA, NFA, GNFA 都可以互相转换。
互相转换
Regular->NFA
按如下图例转换
NFA->FA

从start state开始, 找一步之内能接受对应值的state,将这些state作为新集合,继续寻找。直到没有新的集合出现。
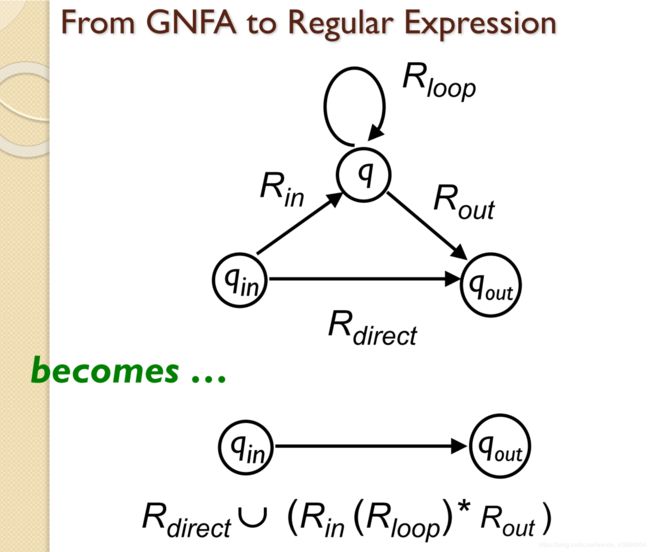
GNFA->regular
简化FA
图例待补充
Convert this into an equivalent FA with the minimum possible number of states:
Final state 作为不同的颜色标记,查看其他行的颜色类型是否一样,不一样的state作为新的颜色。直到不可再分。
正则语言的闭合性
Closure properties of regular languages
complement, union, intersection,concatenation
即正则语言的,补集,并集,交集,级联,仍是正则语言。
context free
Context free -> PushDown
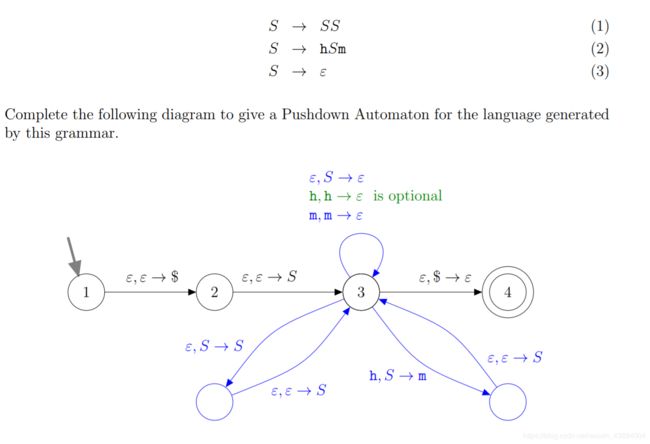
S前的直接读,
S后的先放进stack,然后放S(S stack在顶层),S处理完后最后读取。
NFA->CFG
Chomsky Normal Form
Nonterminal -> Nonterminal Nonterminal
Nonterminal -> terminal
Cocke-Younger-Kasami (CYK) algorithm
Church-Turing Thesis
Any function which can defined by an algorithm can be represented by a Turing Machine.
Evidence:
• different approaches to computability end up in agreement
• long experience, that algorithms can be implemented as programs, and therefore on Turing machines
• no known counterexamples, i.e., no algorithms which seem to be unimplementable