SFFAI1 | 朱时超：图神经网络模型及应用进展【附视频+PPT下载】

关注微信公众号人工智能前沿讲习 回复“朱时超”，获取PPT和视频下载链接

一 、导读

该篇内容介绍基于论文《Relational inductive biases, deep learning, andgraph networks》[14]。

Deepmind尝试把拓扑结构网络图与深度强化学习融合，由此提出了一个新的AI模块——图网络。图网络，是对以前各种对图进行操作的神经网络方法的推广和扩展，学习图网络中实体、关系的向量表示以及构成它们的规则，由于对图进行操作函数的大多通过神经网络实现，所以我们又称之为图神经网络。

在图网络中使用关系归纳偏置学习，保存结构化输入数据之间的拓扑关系，并通过对输入数据的节点处理来跟踪节点中的图结构。因此，图网络具有强大的关系归纳偏置，为操纵结构化知识和生成结构化行为提供了一个直接的界面。结构化的表示和计算可以实现模型的组合泛化能力，这一能力非常重要，可以为更复杂、可解释和灵活的学习和推理模式打下基础。

图网络模型已经在不同的问题领域中进行了探索，包括监督、半监督、无监督和强化学习设置，它们在被认为具有丰富关系结构的任务中是有效的。本讲内容主要包含图网络框架和应用进展。

二、作者简介

朱时超，中国科学院信息工程研究所在读博士，本科毕业于哈尔滨工业大学，目前主要研究兴趣点在图神经网络。欢迎感兴趣的小伙伴一起交流讨论！

三、背景介绍

3.1 图网络相关定义：

3.1.1 图定义

$G=(\mathbf{u},V,E)$，具有全局属性的有向、带属性的多图。

$\mathbf{u}:$全局属性；

$V={\left\{{\mathbf{v}}_i\right\}}_{i=1:N^v}$：节点集合，${\mathbf{v}}_i$表示节点属性；

$E={\left\{\left({\mathbf{e}}_k,r_k,s_k\right)\right\}}_{k=1:N^e}$：边集合，${\mathbf{e}}_k$表示边属性，$r_k$、$S_k$分别表示边的接收和发出节点。

$\mathrm{E}\cdot \mathrm{g}\cdot \mathbf{u}$代表引力场，$V$代表引力场中所有球-属性包含位置、质量、速度，$E$代表不同球之间存在的弹簧-属性包含弹簧数。

3.1.2 图网络

为了学习图网络中实体、关系的向量表示以及构成它们的规则，保存结构化输入数据之间的拓扑关系，并通过对输入数据的节点处理来跟踪节点中的图结构。

3.1.3 最先提出图神经网络的工作

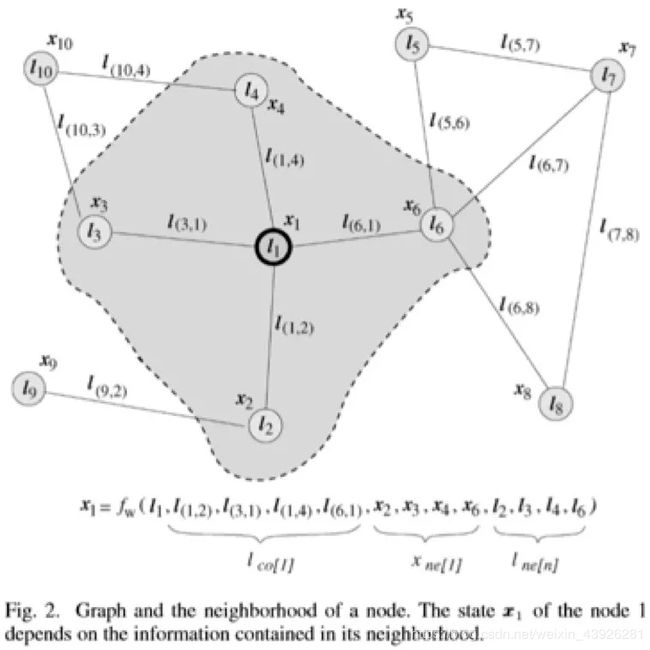
Gori et al.,2005; Scarselli et al., 2005, 2009a[15][16]。05年[15]提出GNNs，主要工作就是去学习到整个图每个节点的状态，$i$节点的状态$x_i$依赖于$j$节点的状态$x_j$同理$j$点也是，二者不断地相互依赖形成一个循环，模型的假设就是我们可以通过循环迭代去求解全图的状态；模型两部分组成：转移transition函数（定义节点之间的关系），输出output函数（每个节点的具体输出），两个函数均由多层前馈神经网络实现，通过模型图被映射到m维欧式空间。同时在09年的论文[16]中验证了图神经网络的计算能力，具有普遍逼近性质，可用于处理结构化数据输入。

发展：17年Bronstein et al.[17]提出深度学习在非欧式空间数据的应用；Gilmer et al.[5]提出了MPNN，统一了多种GNN和GCN；18年Wang et al.[6]提出了NLNN，统一了多种自注意力机制和计算机视觉、图形模型。

3.2 图网络框架：

图网络框架定义了一类用于图形结构表示的关系推理的函数。GN 框架概括并扩展了各种图神经网络（例如 MPNN、NLNN 等），并支持从简单的构建块来构建复杂的结构。GN框架的主要计算单元是 GN block，即 “graph-to-graph” 模块，输入graph，对结构执行计算，输出graph。

3.2.1 计算单元GN block内部结构：三个“update”函数和三个“aggregation”函数。

3.2.2 核心设计原则：

a) 灵活的表示

• i. 属性表示

edge-focused GN：边输出，相关工作有[1][2]，用于实体交互决策分析

node-focused GN：点输出，相关工作有[3][10]，用于物理系统推理

graph-focused GN：图输出，相关工作有[4]，用于视觉场景问答，[5]用于分子属性预测

mixed-and-matched GN：混合边和点输出。

• ii. 图结构表示

知识图谱是显式关系图输入，还有很多图输入为隐式关系表示，需要推理假设。

b) 可配置的内部结构

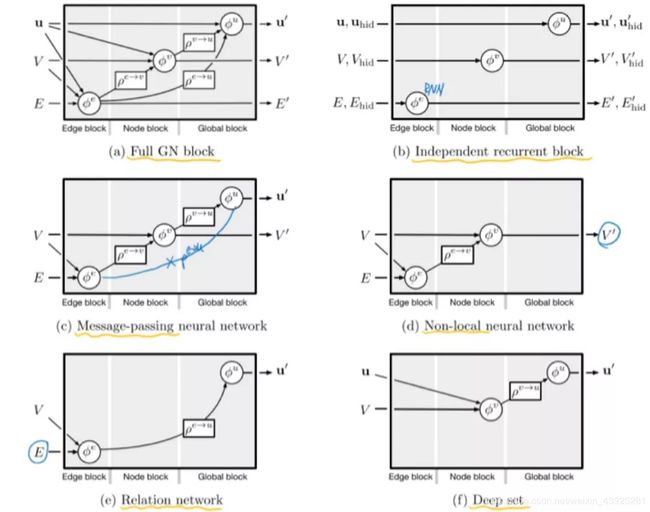
图网络的输入、输出、update函数φ和aggregation函数ρ都是可配置的，通常φ函数实现使用神经网络，ρ函数实现使用逐点求和等方法。目前提出的不同配置的内部结构可以总结为以下六种：Full GN block, Independentrecurrent block, Message-passing neural network (MPNN)[5], Non-local neural networks (NLNN)[6], Relation networks[4], Deep Sets[7].

四、代表性工作

4.1 Message-passingneural network

提出论文：Neural message passing for quantum chemistry([5]Gilmer et al., 2017)，提出了神经网络消息传递的框架，统一了多种结合不同神经网络的消息传递模型。神经网络消息传递框架包含两个阶段：消息传递和读出。消息传递过程执行多轮，每轮操作消息传递函数$M_t\to {\varphi }^e$，逐点求和${\rho }^{e\to v}$，节点更新函数$U_t\to {\varphi }^v$，最后进入读出阶段，执行读出函数$R\to {\varphi }^u$。三个函数可以由不同的函数或者神经网络实现，由此产生了多种变形。注意，全局预测不包括聚合边。

4.2 Non-local neuralnetwork

提出论文：Non-local neuralnetworks (NLNN)[6]，NLNN统一了intra-/self-/vertex-/graph-attention方法，非局部操作模块可以捕获长距离依赖，注意力机制表现在聚合步骤中，一个节点的更新是其邻居节点属性的加权和。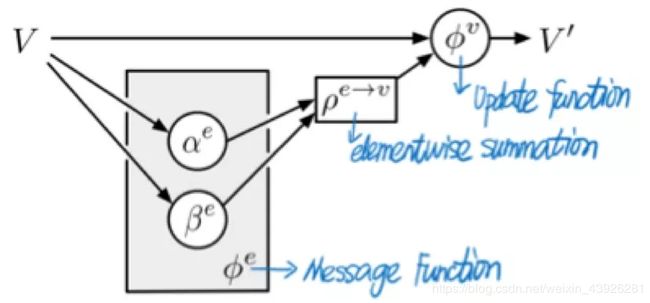

4.3 可组合的多模块结构

图网络通过组合多个GN模块来实现复杂结构，目前提出的有三种不同方式的组合：composition of GNblocks[10], encode-process-decode[2], recurrent GN architecture[3].

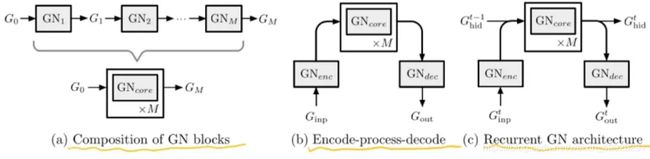
4.4 composition of GNblocks

GNcore周围的白色框代表了重复M次的内部处理子步骤，其中有共享或未共享的GN块。共享配置类似于消息传递MPNN，其中相同的局部更新步骤迭代执行多次进行消息传递。两个好处：这可以解释为将复杂的计算分解为较小的基本步骤；这些步骤还可以用于捕获时间的顺序性。

4.5 encode-process-decode

GN编码输入图产生隐表达，然后由共享的GN核心块重复执行M次，其输出由第三个GN块解码成输出图，其节点、边、全局属性将用于特定任务。提出论文Relationalinductive bias for physical construction in humans and machines[2][edge-focused, full-GN block，encode-process-decode]：物理构建问题-粘合任务（粘合块对以保持整个塔的稳定性），提出了一种深度强化学习智能体，它使用基于对象和关系表示的决策策略，测试其学习粘合任务的能力，关键在于这些结构化表示使用图网络进行实例化，引入了关系归纳偏置，使得在粘合任务上获得了很好的表现。图网络消息传递阶段可以将系统中的力传递到整个结构，从而准确地预测整个系统的稳定性，选择合适的粘合点。

4.6 Recurrent GN architecture

序列设置：编码-处理-解码体系 + 核心GN块（每个时间步骤中重复迭代，随着时间进行展开，可能使用GRU或LSTM体系结构）。

应用：预测图序列，如预测动态系统随时间的状态轨迹。

五、take-home-message

5.1 图网络框架

图：三元组$G=(\mathbf{u},V,E)$

计算单元：GN block，包含三个update函数和三个aggregation函数

5.2 核心设计原则

a.灵活的表示：attributes, graphstructure；

b.可配置的内部结构：full GN block,independent recurrent block, MPNN, NLNN, relation networks, deep sets；

c.可组合的模块结构：composition of GNblocks, encode-process-decode, recurrent GN architecture.

5.3 图网络特点

更一般地说，我们把这些神经网络看作是向将结构化表示与强大的深度学习算法相结合的模型迈出的一步，目的是利用已知结构，学习和推断如何推理和扩展节点和边表示。

组合泛化能力：图网络结构化的表示和计算，可重复使用的基于实体/关系的计算模块，使得GN具有组合泛化能力，大量研究工作也表明了图网络具有这一能力，包括：state predictions[10]、zero-shot transfer[10]、multi-joint agents generalize[3]、decision-making[2]、planning problems、node embedding forunseen data[8]、boolean SAT problems[9]等。

研究方向：将感知数据更为合适地转化为结构化表示；深度图生成模型（Graph-based autoencoders, GraphRNN, MolGAN model[13]）；图结构的自适应调整[1]；图网络的可解释性；整合式的方法学习图网络：人类认知+传统计算科学+工程实践+深度学习。

参考文献

[1] Kipf, T., Fetaya,E., Wang, K.-C., Welling, M., and Zemel, R. (2018). Neural relational inferencefor interacting systems. In Proceedings of the International Conference onMachine Learning (ICML).

[2] Hamrick, J., Allen, K., Bapst, V., Zhu, T., McKee, K.,Tenenbaum, J., and Battaglia, P. (2018). Relational inductive bias for physicalconstruction in humans and machines. In Proceedings of the 40th AnnualConference of the Cognitive Science Society.

[3] Sanchez-Gonzalez,A., Heess, N., Springenberg, J. T., Merel, J., Riedmiller, M., Hadsell, R., andBattaglia, P. (2018). Graph networks as learnable physics engines for inferenceand control. In Proceedings of the 35th International Conference on MachineLearning (ICLR).

[4] Santoro, A.,Raposo, D., Barrett, D. G., Malinowski, M., Pascanu, R., Battaglia, P., andLillicrap, T. (2017). A simple neural network module for relational reasoning.In Advances in Neural Information Processing Systems.

[5] Gilmer, J.,Schoenholz, S. S., Riley, P. F., Vinyals, O., and Dahl, G. E. (2017). Neuralmessage passing for quantum chemistry. arXiv preprint arXiv:1704.01212.

[6] Wang, X.,Girshick, R., Gupta, A., and He, K. (2018c). Non-local neural networks. InProceedings of the Conference on Computer Vision and Pattern Recognition(CVPR).

[7] Zaheer, M.,Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. R., and Smola, A. J.(2017). Deep sets. In Advances in Neural Information Processing Systems, pages3394–3404.

[8] Hamilton, W.,Ying, Z., and Leskovec, J. (2017). Inductive representation learning on largegraphs. In Advances in Neural Information Processing Systems, pages 1025–1035.

[9] Selsam, D., Lamm,M., Bunz, B., Liang, P., de Moura, L., and Dill, D. L. (2018). Learning a satsolver from single-bit supervision. arXiv preprint arXiv:1802.03685.

[10]Battaglia, P.,Pascanu, R., Lai, M., Rezende, D. J., et al. (2016). Interaction networks forlearning about objects, relations and physics. In Advances in NeuralInformation Processing Systems, pages 4502–4510.

[11]O˜noro-Rubio, D.,Niepert, M., Garc´ıa-Dur´an, A., Gonz´alez-S´anchez, R., and L´opez-Sastre, R.J. (2017). Representationlearning for visual-relational knowledge graphs. arXiv preprint arXiv:1709.02314.

[12]Hamaguchi, T.,Oiwa, H., Shimbo, M., and Matsumoto, Y. (2017). Knowledge transfer forout-ofknowledge-base entities: A graph neural network approach. In Proceedingsof the International Joint Conference on Artificial Intelligence (IJCAI).

[13]De Cao, N. andKipf, T. (2018). MolGAN: An implicit generative model for small moleculargraphs. arXiv preprint arXiv:1805.11973.

[14]Battaglia P W,Hamrick J B, Bapst V, et al. (2018). Relational inductive biases, deeplearning, and graph networks. arXiv:1806.01261.

[15]Scarselli, F.,Gori, M., Tsoi, A. C., Hagenbuchner, M., and Monfardini, G. (2009b). The graphneural network model. IEEE Transactions on Neural Networks, 20(1):61–80.

[16]Scarselli, F.,Gori, M., Tsoi, A. C., Hagenbuchner, M., and Monfardini, G. (2009a).Computational capabilities of graph neural networks. IEEE Transactions onNeural Networks, 20(1):81–102.

[17]Bronstein, M. M.,Bruna, J., LeCun, Y., Szlam, A., and Vandergheynst, P. (2017). Geometric deeplearning: going beyond euclidean data. IEEE Signal Processing Magazine,34(4):18–42.