1.动态规划
一个问题如果具有重复子问题,那么可以用动态规划求解,从而减少大量重复计算。
2.数塔问题
问:从第一层走到最后一层所有路径上的数字相加后最大和是多少?
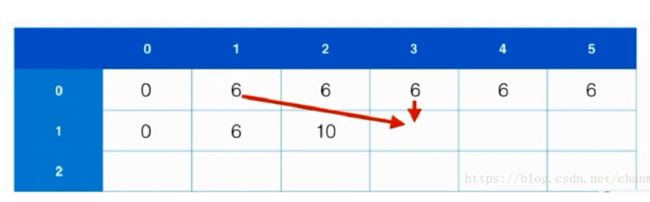
令dp[i][j]表示第i层第j个数字当前的最大和,则状态转移方程:
边界:,使用choice[i][j]数组记录每一个节点是由下层哪个节点得到的,从而回溯构造结果
程序代码:
#include
#include
using namespace std;
const int maxn = 100;
int numTower[maxn][maxn];
int dp[maxn][maxn];
int choice[maxn][maxn] = {0};
int main()
{
int n;
scanf("%d",&n); //²ãÊý
for(int i=0;i=0;i--)
for(int j=0;j<=i;j++){
if(dp[i+1][j] >= dp[i+1][j+1]){
dp[i][j] = dp[i+1][j] + numTower[i][j];
choice[i][j] = 1;
}
else{
dp[i][j] = dp[i+1][j+1] + numTower[i][j];
choice[i][j] = 2;
}
}
printf("%d\n",dp[0][0]);
int j = 0;
for (int i = 0; i < n; ++i)
{
printf("%d",numTower[i][j] );
if (choice[i][j] == 2)
{
j++;
}
if(i != n-1)
printf(" ");
}
}
3.最大连续子序列和
问题:给定K个整数的序列{ N1, N2, ..., NK },其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj },其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个,例如给定序列{ -2, 11, -4, 13, -5, -2 },其最大连续子序列为{ 11, -4, 13 },最大和为20。现在增加一个要求,即还需要输出该子序列的第一个和最后一个元素。
样例输入
5
-3 9 -2 5 -4
3
-2 -3 -1
0
样例输出
12 9 5
0 -2 -1
令dp[i]表示以i结尾的数字当前最大和,状态转移方程:
边界:。
程序代码:
#include
#include
#include
using namespace std;
const int maxn = 10010;
int a[maxn];
int dp[maxn];
int choice[maxn];
int main(int argc, char const *argv[])
{
int k;
while((scanf("%d",&k)) && k){
for(int i=0;i= dp[i - 1] + a[i]){
dp[i] = a[i];
choice[i] = 1;
}else{
dp[i] = dp[i-1] + a[i];
choice[i] = 2;
}
if(dp[i] > dp[maxInd])
maxInd = i;
}
if(dp[maxInd] < 0){
printf("%d %d %d\n",0,a[0],a[k-1] );
}else{
int p = maxInd;
while(choice[p] == 2)
p--;
printf("%d %d %d\n",dp[maxInd],a[p],a[maxInd] );
}
}
return 0;
}
4.最长不下降子序列(LIS)
问题:在一个数字序列中,找到一个最长的子序列(可以不连续),使得这个子序列是不下降的,例如现有序列A={1,2,3,-1,-2,7,9},其最长不下降子序列是{1,2,3,7,9},长度为5。
令dp[i]表示以i结尾的序列当前最长不下降子序列的长度,则状态转移分为两种情况:
- 如果存在A[i]之前的元素Aj,使得且,则A[i]可跟在A[j]后形成更长的序列
- 如果不存在,那么A[i]只能自己形成一条LIS,长度为1
状态转移方程:
初始状态:
程序代码:
#include
#include
#include
using namespace std;
const int maxn = 10010;
int a[maxn];
int dp[maxn];
int choice[maxn];
int main(int argc, char const *argv[])
{
int k;
while((scanf("%d",&k)) && k){
for(int i=0;i= dp[i - 1] + a[i]){
dp[i] = a[i];
choice[i] = 1;
}else{
dp[i] = dp[i-1] + a[i];
choice[i] = 2;
}
if(dp[i] > dp[maxInd])
maxInd = i;
}
if(dp[maxInd] < 0){
printf("%d %d %d\n",0,a[0],a[k-1] );
}else{
int p = maxInd;
while(choice[p] == 2)
p--;
printf("%d %d %d\n",dp[maxInd],a[p],a[maxInd] );
}
}
return 0;
}
5.最长公共子序列(LCS)
给定两字符串A、B,如sadstory和adminsorry,其最长公共子序列为adsory。
令dp[i][j]为A串的第i号字符和B串的第j号字符之前的LCS长度,状态转移有以下两种情况:
1.如果,则
2.否则,
状态转移方程:
边界:
注:使用回溯法可求得具体的公共子串(待补)
程序代码:
#include
#include
#include
using namespace std;
const int maxn = 1000;
char A[maxn],B[maxn];
int dp[maxn][maxn];
int main()
{
gets(A + 1); gets(B + 1);
int lenA = strlen(A + 1);
int lenB = strlen(B + 1);
for(int i=0;i<= lenA;i++)
dp[i][0] = 0;
for(int i=0;i<= lenB;i++)
dp[0][i] = 0;
//dp[i][j] = dp[i-1][j-1] + 1,A[i] = A[j]
//dp[i][j] = max(dp[i-1][j],dp[i][j-1])
for(int i=1;i<= lenA;i++)
for(int j=1;j<= lenB;j++)
if(A[i] == B[j])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
printf("%d\n",dp[lenA][lenB]);
}
6.最长回文子串
问题:给定一字符串S,求其最长回文子串长度
如PATZJUJZTACCBCC,最长回文子串为ATZJUJZTA,长度为9
令dp[i][j]表示区间为[i,j]串是否是回文串,状态转移分为以下两种情况:
1.若,那么如果区间[i+1,j-1]内的串仍为回文串的话,那么区间为[i,j]的串即为回文串
2.若,那么区间为[i,j]的串肯定不是回文串
状态转移方程:
边界:
注意:枚举方法
如果按照i,j从小到大的顺序枚举,无法保证dp[i+1][j-1]被计算过,因为只初始化了长度为1和2的串,因此可以按串长度即区间长度进行枚举。
程序代码:
#include
#include
#include
using namespace std;
int const maxn = 1000;
char A[maxn];
int dp[maxn][maxn];
int main()
{
gets(A);
int len = strlen(A);
for(int i=0;i
7.DAG最长路(待)
8.0-1背包问题
问题描述:有n件物品,每件物品的重量为w[i],价值为c[i]。现有一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大,其中每种物品只有一件。
令dp[i][v]表示前i种物品恰好能放入重量为v的背包所能得到的总价值,状态转移有以下两种情况:
1.选择第i种物品,那么问题转化为前i-1种物品能够放入重量为v-w[i]的背包所能获得的最大价值。
2.不选择第i种物品,那么当前最大价值即等于前i-1种物品能够放入重量为v的背包所能获得的最大价值。
状态转移方程:
边界状态:
空间复杂度的优化:
注意到dp[i][j]的计算只是依赖于i-1阶段的V个状态,而不依赖于i-1之前的状态,因此可以通过滚动数组策略来去掉物品的维度,状态方程:
当前第i阶段只依赖i-1阶段的值,因此在枚举重量v的时候只能
逆序枚举,否则会当前i阶段的值会覆盖i-1阶段的值(后面枚举需要用到)。
程序代码:
#include
#include
#include
using namespace std;
const int maxn = 100; //物品最大数
const int maxv = 1000; //背包最大重量
//每件物品的重量,每件物品的价值,重量为v的背包所能装物品的最大价值
int w[maxn], c[maxn], dp[maxv];
int selected[maxn]; //记录每个物品是否被选择
int main(int argc, char const *argv[])
{
int n,V;
scanf("%d%d",&n,&V);
for(int i=0;i=w[i];v--){
dp[v] = max(dp[v],dp[v - w[i]] + c[i]);
}
}
//寻找最大的dp[v]
int k = 0;
for(int v=0;v<=V;v++){
if(dp[v] > dp[k])
k = v;
}
printf("%d\n", dp[k]);
return 0;
}
9.完全背包问题
问题描述:有n种物品,每种物品的单件重量为w[i],价值为c[i]。现有一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大,其中每种物品都有无穷件。
令dp[i][v]表示前i件物品恰好放入容量为v的背包中所能获得的最大价值,和0-1背包的区别在于:
1.不放第i件物品,那么,同0-1背包
2.放第i件物品,那么,这里dp[i][v]依赖阶段i的v-w[i]的状态,因为物品数量无限,所以可以重复的放物品i
状态转移方程:
边界状态:
同样,可以用滚动数组来去掉物品维度,此时需要正序枚举背包容量,因为阶段i的值依赖当前阶段i,需要使用覆盖的数据,状态转移方程:
10.完全背包可行方案数的问题
问题描述:传统地,一个货币系统是由1,5,10,20 或 25,50, 和 100的单位面值组成的,现用这些硬币支付面值为A的商品,问有多少种不同的方案,输出字典顺序最小的方案,这些硬币无穷多个。
问题特点:相当于求下列方程解的个数:
其中表示n个硬币的面值,表示组合方案。
令dp[i][v]表示前i个硬币恰能组成面值为v的方案数,则状态转移方程:
初始化:
使用滚动数组,状态转移方程可转化为:
进行正序枚举面值v即可
程序代码:
#include
#include
#include
using namespace std;
/*
1.此类问题为完全背包的可行解个数问题,需要掌握
2.令dp[i][v]表示前i个物品恰能装满重量为w的方案数
3.状态转移方程:dp[i][v] = dp[i-1][v] + dp[i][v-w[i]],dp[:][0] = 1
4.讨论:第一种状态转移:不选物品i,状态转移取决于i-1阶段
第二种状态转移:选择物品i,由于物品i的个数不受限制,因此
状态转移取决于第i阶段,可以选择多个物品i,但会受到容量v的限制
5.可以将上述二维状态转移方程利用滚动数组变成一维
6.进行正序dp
*/
const int maxn = 30;
const int maxm = 10010;
long long dp[maxm],w[maxn];
int main(int argc, char const *argv[])
{
int n,V;
scanf("%d%d",&n,&V);
for(int i=1;i<=n;i++)
scanf("%lld",&w[i]);
//初始化
dp[0] = 1;
for(int i=1;i<=V;i++)
dp[i] = 0;
for(int i=1;i<=n;i++){
for(int v=w[i];v<=V;v++)
dp[v] = dp[v] + dp[v-w[i]];
}
printf("%lld\n",dp[V] );
return 0;
}
11.非完全背包问题
问题描述:有1元、5元、50元、100元、500元的硬币各1、5、10、50、100、500枚。现在要用这些硬币来支付A元,有多少种支付方案。并且输出字典顺序最小的方案。