李宏毅机器学习（五）

此篇博文参考李航-《统计学习方法》第五章决策树；《机器学习实战》第三章。

一、信息增益

在机器学习决策树算法中，涉及到特征选择。特征选择目的是选择对训练数据具有分类能力的特征，因此可以提高决策树学习效率。通常特征选择的准则是信息增益或信息增益比。

1、熵(entropy)

熵(entropy)：信息量大小的度量，即表示随机变量不确定性的度量。 设$X$是取有限值的离散随机变量，概率分布为：
$$P(X=x_i)=p_i,i=1,2,...,n\text{\hspace{1em}(1.1)}$$
则随机变量$X$的熵的定义为：
$$H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i\text{\hspace{1em}(1.2)}$$
若$p_i=0$，则定义为$0log0=0$。上式中的对数以2为底或以e为底(自然对数)，这是熵的单位分别称做比特（bit）或纳特（nat）。由定义可知，熵只依赖于$X$的分布，而与$X$的取值无关，所以也可将$X$的熵记作$H(p)$，即：
$$H(p)=-\sum _{i=1}^n{p}_{i}log{p}_i\text{\hspace{1em}(1.3)}$$
熵越大，随机变量的不确定性越大：
$$0\le H(p)\le logn\text{\hspace{1em}(1.4)}$$
当随机变量只取两个值，例如0，1时，即$X$的分布为：
$$P(X=1)=p,P(X=0)=1-p,0\le p\le 1\text{\hspace{1em}(1.5)}$$
熵为：
$$H(p)=-lo{g}_{2}p-(1-p)lo{g}_2(1-p)\text{\hspace{1em}(1.6)}$$
这时，熵$H(p)$随概率$p$变化的曲线如图所示：

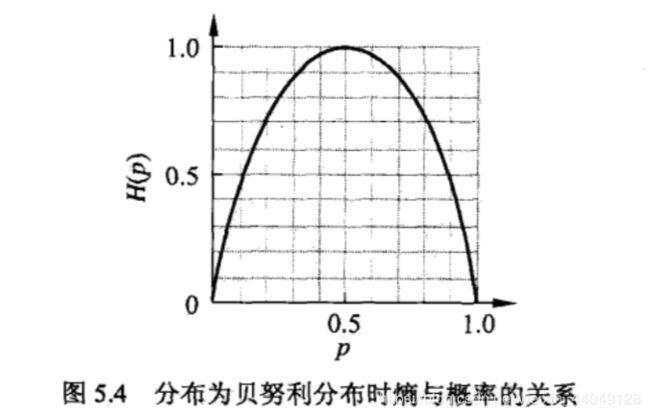
当$p=0$或1时，熵$H(p$)为0，表示随机变量完全没有不确定性。当$p=0.5$时，不确定性最大。

2、条件熵(conditional entropy)

设有随机变量$(X,Y)$,其联合概率分布为：
$$P(X=x_i,Y=y_j)=p_{ij},i=1,2...,n;j=1,2,...,m$$
条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性。随机变量$X$给定的条件下随机变量$Y$的条件熵(conditional entropy)：$H(Y|X)$，定义为$X$给定条件下$Y$的条件概率分布的熵对$X$的数学期望：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)\text{\hspace{1em}(1.7)}$$
这里$p_i=P(X=x_i)$，i=1,2,…n.

3、经验熵和经验条件熵

当熵和条件熵中的概率由数据估计(特别是极大似然估计得到时，所对应的熵与条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy )。

4、互信息(mutual information)

特征$A$对训练数据集$D$的信息增益$g(D,A)$, 定义为集合$D$的经验熵$H(D)$与特征$A$给定条件下
$D$的经验条件熵$H(D|A)$之差，即
$$g(D,A)=H(D)-H(D|A)\text{\hspace{1em}(1.8)}$$
一般地，熵与条件熵之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。

5、推导公式

1. 条件熵定义式：
   

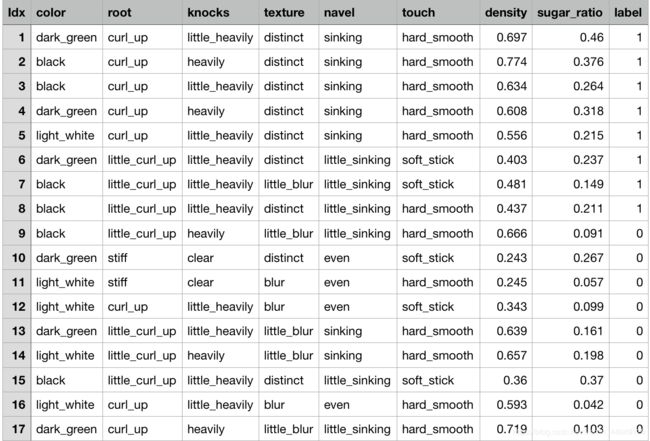
6、计算数据集香农熵

1. 数据集：
   
2. 代码：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# 导入所需包
import numpy as np
import pandas as pd

# 读取数据集
data = pd.read_csv('watermelon_3a.csv')

def cacl_shannonEnt(dataSet):
    numEntries = len(dataSet)
    # 分类标签
    labelCounts = {}

    # 为所有可能分类创建字典
    for i in range(numEntries):
        label = dataSet[i][-1]
        labelCounts[label] = labelCounts.get(label, 0) + 1
    shannonEnt = 0.0

    for counts in labelCounts.values():
        prob = counts / numEntries
        # 以2为底求对数
        shannonEnt -= prob * np.log2(prob)
    return shannonEnt
    
dataset = data.values
shannonEnt = cacl_shannonEnt(dataset)
print(shannonEnt)
# 0.997502546369