Java数据结构之克里斯卡尔算法(Kruskal算法)
介绍
Kruskal算法与Prim算法不同,Prim是以顶点为向导,通过遍历顶点不断寻找与之相连的最小的权值边,从而找到最小生成树。Kruskal算法是以边为向导,依次找出权值最小的边建立最小生成树,每次新增的边要保证不能使生成树构成回路,直到遍历完所有的边为止。
核心思想
Kruskal的核心算法即在如何验证所添加的边是否与已添加的边构成回路,从而进行边的取舍。如图1所示,根据左图构建数组edges[]用于保存每条边对象,该对象包括begin、end和weight属性,分别表示当前边的起始顶点、终点和权值。对edges进行从小到大的排序后,得到如右图所示的数组。我们从小到大选择权值最小的边,每添加一条边,则图中会连接两个顶点。我们只需保证每次新添加的边不会与之前添加的边构成回路,那么,当所有的边遍历结束后,就形成了最小生成树。

如何验证回路
我们构建一个特殊的长度为边数的parent数组,该数组的角标表示某条边的起点,值为该边的终点,初始化时parent数组全为0,即表示没有一条边加入。我们通过角标,即起始顶点,可以找到该起始顶点所连接的终点,即邻接点;再以该终点作为新的起始顶点,又可以找到下一个终点。当找到的终点为0时,表示该以该终点为起点的顶点不存在邻接点;当以边的起点为起点找到的最终终点,与以边的终点为起点找到的最终终点相等时,说明该边会与之前的边构成回路。下面通过图1中的图来说明。
当遍历到edge[0]时,parent[4]=0,表示尚未加入以v4为顶点的边,故将edge[0]边的起始顶点和终点加入到parent数组中,此时parent=[0, 0, 0, 0, 7, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],即parent[4]=7,表示存在以顶点v4为起点,v7为终点的通路,这里即是edges[0]边。依次向下遍历,由于parent数组初始为0,故在edge[6]之前不存在构成回路的边,如下图所示,此时parent=[1, 5, 8, 7, 7, 8, 0, 0, 6, 0, 0, 0, 0, 0, 0]。

当遍历到edge[7]时,edges[7]的起始顶点为5,我们以edges[7]的起始顶点为起点,在parent数组中查找其最终终点,有如下过程:
parent[5]=8 --> parent[8]=6 --> parent[6]=0 故尚不存在以v6为起始顶点的边,最终终点为v6
注意:此处从parent[5]=8并不表示顶点v5和v8是直接相连的,而是表示v5顶点最终会通过某种连接连通到v8,以此类推,我们可以得知v5最终会连通到v6。
以edge[7]的终点为起点,在parent数组中查找器最终终点,有如下过程:
parent[6]=0 故尚不存在以v6为起始顶点的边,最终终点即为起点v6
此时,我们发现以edges[7]的起点和终点的搜索结果相等,故可以得到,当加入edges[7]边时,会与图中已经存在的边构成回路,所以我们将其舍弃,如下图所示。
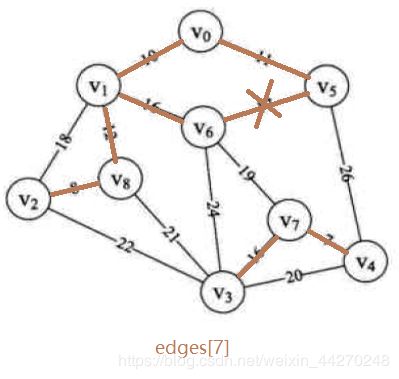
以此类推,当所有的边都遍历完成之后,图中的顶点所构成的回路即为最小生成树,如下图:
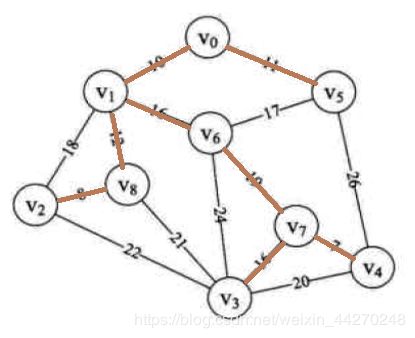
代码实现
package Kruskal;
/**
* 克鲁斯卡尔算法
* @author asus
*/
public class Kruskal {
private Edge[] edges; // 按权值从小到大排序后的边数组
private int edgeSize; // 边数
public Kruskal(int edgeSize) {
this.edgeSize = edgeSize;
edges = new Edge[edgeSize];
}
//定义边的内部类
class Edge {
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
public int getBegin() {
return begin;
}
public void setBegin(int begin) {
this.begin = begin;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
}
//通过邻接矩阵创建数组
public Edge[] createEdgeArray(int[][] matrix) {
int k = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = i + 1; j < matrix[i].length; j++) {
int m = matrix[i][j];
if (matrix[i][j] == Integer.MAX_VALUE)
continue;
edges[k] = new Edge(i, j, matrix[i][j]);
k++;
}
}
for (int i = 0; i < edges.length; i++) {
for (int j = i + 1; j < edges.length; j++) {
if (edges[j].weight < edges[i].weight) {
Edge e = edges[i];
edges[i] = edges[j];
edges[j] = e;
}
}
}
return edges;
}
public void miniSpanTreeKruskal() {
int m, n, sum = 0;
int[] parent = new int[edgeSize];// 用于验证是否构成回路,角标为某条边的起点,值为该边的终点
for (int i = 0; i < parent.length; i++) {
parent[i] = 0;
}
for (int i = 0; i < parent.length; i++) {
m = find(parent, edges[i].begin);// 以edges[i]边的起点为检索起点,找到其可以连接到的最终终点
n = find(parent, edges[i].end);// 以edges[i]边的终点为检索起点,找到其可以连接到的最终终点
if (m != n) {// 新加入的edges[i]边不会和已加入的边构成回路
parent[m] = n;
System.out.println("连接起点:" + edges[i].begin + ",连接终点:" + edges[i].end + ",权值为:" + edges[i].weight);
sum += edges[i].weight;
} else {
System.out.println("边" + i + "构成了回路");
}
}
System.out.println("sum:" + sum);
}
/**
* 在图中以node为搜索起点进行检索,最终返回检索到的终点。即表示,从起点node开始,不论以何种路径检索,最终会连接到终点。
*
* @param parent 用于检验是否构成回路的数组
* @param node 起始顶点,在parent中为角标
* @return 返回终点
*/
private int find(int[] parent, int node) {
while (parent[node] > 0) {// 已经添加了边
node = parent[node];// 以检索到的终点为新的起点继续检索
}
return node;
}
}
测试实例
package Kruskal;
import Kruskal.Kruskal.Edge;
public class KruskalDemo {
public static void main(String[] args) {
int MAX_WEIGHT = Integer.MAX_VALUE;//定义无效权值
int[][] Matrix = new int[9][]; //邻接矩阵
//邻接矩阵初始化
Matrix[0] = new int[] {0,10,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,11,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT};
Matrix[1] = new int[] {10,0,18,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,16,MAX_WEIGHT,12};
Matrix[2] = new int[] {MAX_WEIGHT,MAX_WEIGHT,0,22,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,8};
Matrix[3] = new int[] {MAX_WEIGHT,MAX_WEIGHT,22,0,20,MAX_WEIGHT,24,16,21};
Matrix[4] = new int[] {MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,20,0,26,MAX_WEIGHT,7,MAX_WEIGHT};
Matrix[5] = new int[] {11,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,26,0,17,MAX_WEIGHT,MAX_WEIGHT};
Matrix[6] = new int[] {MAX_WEIGHT,16,MAX_WEIGHT,26,MAX_WEIGHT,17,0,19,MAX_WEIGHT};
Matrix[7] = new int[] {MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,16,7,MAX_WEIGHT,19,0,MAX_WEIGHT};
Matrix[8] = new int[] {MAX_WEIGHT,12,8,21,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,0};
Kruskal k = new Kruskal(15);
Edge[] e = k.createEdgeArray(Matrix);//可以打印e以检验是否排序,这里省略
k.miniSpanTreeKruskal();
}
}
输出结果
连接起点:4,连接终点:7,权值为:7
连接起点:2,连接终点:8,权值为:8
连接起点:0,连接终点:1,权值为:10
连接起点:0,连接终点:5,权值为:11
连接起点:1,连接终点:8,权值为:12
连接起点:3,连接终点:7,权值为:16
连接起点:1,连接终点:6,权值为:16
边7构成了回路
边8构成了回路
连接起点:6,连接终点:7,权值为:19
边10构成了回路
边11构成了回路
边12构成了回路
边13构成了回路
边14构成了回路
sum:99