【Electromagnetic Field and Electromagnetic Wave】2 —— 透彻理解梯度、散度与旋度
文章目录
- 一、标量场的梯度
- 1.1 从等值面与方向导数说起
- 1.2 梯度的意义与计算
- 二、矢量场的散度
- 2.1 从通量说起
- 2.2 散度及其推导
- 2.3 高斯散度的定理
- 三、矢量场的旋度
- 3.1 先从环量说起:
- 四、梯度、旋度、散度的关系
一、标量场的梯度
1.1 从等值面与方向导数说起
方向导数(标量) 的计算:比如说我们给出了一个标量场函数: u ( x , y , z ) u(x, y, z) u(x,y,z),下面要计算这个标量场内一点 M 0 M_0 M0 处的方向导数,计算公式是这样的: ∂ u ∂ l = ∂ u ∂ x c o s α + ∂ u ∂ y c o s β + ∂ u ∂ z c o s γ \frac{\partial{u}}{\partial{l}} = \frac{\partial{u}}{\partial{x}}cosα + \frac{\partial{u}}{\partial{y}}cosβ + \frac{\partial{u}}{\partial{z}}cosγ ∂l∂u=∂x∂ucosα+∂y∂ucosβ+∂z∂ucosγ
方向导数反应的是在标量场里面,从 M M M 点开始沿着某一方向 l → \overrightarrow{l} l 距离的变化率。
那么,如果我们知道了方向 l → \overrightarrow{l} l,是需要会计算方向余弦的。计算方法是:比如我们要计算 c o s α cosα cosα,(也即是 x x x 方向的方向余弦)那么我们就用向量 ( 1 , 0 , 0 ) (1, 0, 0) (1,0,0) 去我们的方向向量 l → \overrightarrow{l} l 做点乘运算,就可以把 c o s α cosα cosα 求出来。
1.2 梯度的意义与计算
梯度,他是一个矢量。它的计算公式如下: g r a d u → = ∂ u ∂ x a x → + ∂ u ∂ y a y → + ∂ u ∂ z a z → \overrightarrow{grad \space u} = \frac{\partial{u}}{\partial{x}}\overrightarrow{a_x} + \frac{\partial{u}}{\partial{y}}\overrightarrow{a_y} + \frac{\partial{u}}{\partial{z}}\overrightarrow{a_z} grad u=∂x∂uax+∂y∂uay+∂z∂uaz
如果当 l → \overrightarrow{l} l 和梯度的方向一致,那么就表示是场函数 u ( x , y , z ) u(x,y,z) u(x,y,z) 变化最快的方向,最大变化率就是梯度的模值: ∣ g r a d u → ∣ = ∂ u ∂ x 2 + ∂ u ∂ y 2 + ∂ u ∂ z 2 |\overrightarrow{grad \space u} | = \sqrt{\frac{\partial{u}}{\partial{x}}^2+\frac{\partial{u}}{\partial{y}}^2+\frac{\partial{u}}{\partial{z}}^2} ∣grad u∣=∂x∂u2+∂y∂u2+∂z∂u2
而标量场沿着任意方向的方向导数就等于梯度在这个方向上的投影!,表示为: ∂ u ∂ l = g r a d u → ⋅ a l → \frac{\partial{u}}{\partial{l}} = \overrightarrow{gradu} \sdot \overrightarrow{a_l} ∂l∂u=gradu⋅al
二、矢量场的散度
2.1 从通量说起
首先,什么是通量呢?—— 简单点说,就是单位时间内通过某一面积的曲面的量。
我们以下面这个不封闭的曲面为例:我们可以将这个大曲面(设面积为 S S S)分割成若干个子区域对吧,每一个子区域的面积是 d S dS dS, d S dS dS 曲面的单位法向矢量是 a n → \overrightarrow{a_n} an。这里还需要说明一件事情:
对于不封闭的曲面来说,其单位法向矢量与曲面构成右手螺旋定则。因此,下图中的 a n → \overrightarrow{a_n} an 方向向上
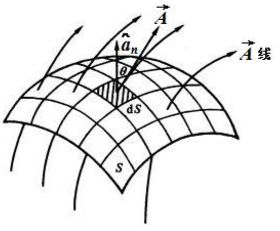
通过 d S dS dS 面的量,我们可以用 A → \overrightarrow{A} A • a n → \overrightarrow{a_n} an表示,那么根据积分的定义,通过整个面积为 S S S 的曲面的量就可以表示成 Φ = ∬ S A → ⋅ a n → d S (1) Φ=\iint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS\tag{1} Φ=∬SA⋅an dS(1)
其中, A → \overrightarrow{A} A • a n → \overrightarrow{a_n} an表示矢量 A → \overrightarrow{A} A 在 a n → \overrightarrow{a_n} an方向上的投影。那么,类似地,如果这个曲面是面积为 S S S 的闭合曲面,那么有 Φ = ∯ S A → ⋅ a n → d S (2) Φ = \oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS\tag{2} Φ=∬SA⋅an dS(2)
式(1)、(2)就是我们所说的通量了!注意:从上式的形式可以看出:通量是个标量!
2.2 散度及其推导
下面我们就想啊:假如是闭合曲面,讲道理净通量 Φ Φ Φ 应该是 0,也就是说进入闭合曲面的矢量线有几条,那么穿出去的应该也是多少条。但是,常常会有下面的情况:
- 如果 Φ > 0 Φ >0 Φ>0 ,说明这个闭合曲面内部还有一个“发射”的东西(我们称之为能量正源),使得穿出曲面的矢量线条数增加了。
- 如果 Φ > 0 Φ >0 Φ>0 ,说明这个闭合曲面内部还有一个“吸收”的东西(我们称之为能量负源),它会吸收穿入曲面的一些 “能量”(矢量线),使得穿出曲面的矢量线条数减小了。
如果我们再定义一个通量源密度,也就是单位体积内的通量大小。 ∯ S A → ⋅ a n → d S V \frac{\oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS}{V} V∬SA⋅an dS
当我们将曲面所包围的体积逐渐缩小的时候,曲面也渐渐逼近通量源,当 V → 0 V\to0 V→0时,若极限存在,我们就定义这个极限就是我们所说的散度: d i v A → = lim V → 0 ∯ S A → ⋅ a n → d S V div\overrightarrow{A} = \lim_{V\to0}\frac{\oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS}{V} divA=V→0limV∬SA⋅an dS
这就是散度的定义。说明:散度也是一个标量!
但是,在应用过程中,使用定义式直接计算散度相当麻烦,我们下面给出一个更好用的式子:
先看下面的情况:
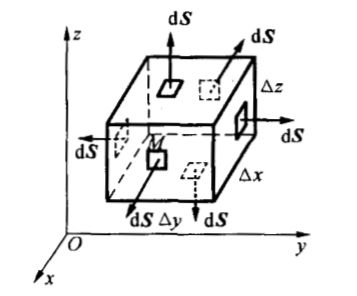
我们看这个长方体的最左下角的 M M M,定义 M ( x , y , z ) M(x, y, z) M(x,y,z),长方体的长宽高分别是 △ y , △ x , △ z △y, △x, △z △y,△x,△z
在 M M M 点处的矢量为: A → = A x a x → + A y a y → + A z a z → \overrightarrow{A} = A_x\overrightarrow{a_x}+A_y\overrightarrow{a_y}+A_z\overrightarrow{a_z} A=Axax+Ayay+Azaz 这里特别注意: A x , A y , A z A_x, A_y,A_z Ax,Ay,Az都是 ( x , y , z ) (x,y,z) (x,y,z) 三者的函数!
我们下面先看看长方体前面的通量: ∯ S 1 A → ⋅ a f r o n t → d S = ∯ S 1 A x d S = A x ( x + △ x , y , z ) △ y △ z \oiint_{S1}\overrightarrow{A}\sdot \overrightarrow{a_{front}} dS = \oiint_{S1}A_xdS = A_x(x+△x, y, z)△y△z ∬S1A⋅afrontdS=∬S1AxdS=Ax(x+△x,y,z)△y△z
下面,我们回忆一下泰勒公式是怎么用的,下面是 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处的泰勒展开: f ( x ) = f ( x 0 ) 0 ! + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \cdots f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯
那么,类似地使用变量代换,将上式的 x x x 代换成 x + △ x x+△x x+△x, x 0 x_0 x0 换成 x x x, f ( ) f() f()函数使用 A x ( ) A_x() Ax()替换,得: A x ( x + △ x , y , z ) = A x ( x , y , z ) + ∂ A x ( x , y , z ) ∂ x △ x + 1 2 ∂ 2 A x ( x , y , z ) ∂ x 2 △ x 2 + ⋯ A_x(x+△x,y,z) =A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x + \frac{1}{2}\frac{\partial^2 A_x(x,y,z)}{\partial x^2}△x^2+\cdots Ax(x+△x,y,z)=Ax(x,y,z)+∂x∂Ax(x,y,z)△x+21∂x2∂2Ax(x,y,z)△x2+⋯
因此,我们可以得到一个近似表达: A x ( x + △ x , y , z ) ≈ A x ( x , y , z ) + ∂ A x ( x , y , z ) ∂ x △ x A_x(x+△x,y,z) ≈ A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x Ax(x+△x,y,z)≈Ax(x,y,z)+∂x∂Ax(x,y,z)△x
因此,前面的净通量就近似表示成: ∯ S 1 A → ⋅ a f r o n t → d S ≈ A x ( x , y , z ) △ y △ z + ∂ A x ( x , y , z ) ∂ x △ x △ y △ z \oiint_{S1}\overrightarrow{A}\sdot \overrightarrow{a_{front}} dS ≈A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z ∬S1A⋅afrontdS≈Ax(x,y,z)△y△z+∂x∂Ax(x,y,z)△x△y△z
那么,我们再看看后面得通量:由于 A x a x → A_x\overrightarrow{a_x} Axax 的方向是沿着 x x x 轴的正方向,因此与 a b a c k → \overrightarrow{a_{back}} aback 的方向相反,那么得到的通量结果是: ∯ S 2 A → ⋅ a b a c k → d S = − A x ( x , y , z ) △ y △ z \oiint_{S2}\overrightarrow{A}\sdot \overrightarrow{a_{back}} dS = -A_x(x,y,z)△y△z ∬S2A⋅abackdS=−Ax(x,y,z)△y△z
那么,我们就可以得到前后两个面的净通量: Φ f r o n t + Φ b a c k = A x ( x , y , z ) △ y △ z + ∂ A x ( x , y , z ) ∂ x △ x △ y △ z − A x ( x , y , z ) △ y △ z = ∂ A x ( x , y , z ) ∂ x △ x △ y △ z \begin{aligned} Φ_{front} + Φ_{back} &= A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z - A_x(x,y,z)△y△z\\ &=\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z \end{aligned} Φfront+Φback=Ax(x,y,z)△y△z+∂x∂Ax(x,y,z)△x△y△z−Ax(x,y,z)△y△z=∂x∂Ax(x,y,z)△x△y△z
那么,如果我们求出前后左右上下六个面的净通量,就可以表示成: Φ t o t a l = ∂ A x ( x , y , z ) ∂ x △ x △ y △ z + ∂ A y ( x , y , z ) ∂ y △ x △ y △ z + ∂ A z ( x , y , z ) ∂ z △ x △ y △ z Φ_{total} = \frac{\partial A_x(x,y,z)}{\partial x}△x△y△z + \frac{\partial A_y(x,y,z)}{\partial y}△x△y△z + \frac{\partial A_z(x,y,z)}{\partial z}△x△y△z Φtotal=∂x∂Ax(x,y,z)△x△y△z+∂y∂Ay(x,y,z)△x△y△z+∂z∂Az(x,y,z)△x△y△z
令体积微元 △ V = △ x △ y △ z △V = △x△y△z △V=△x△y△z,因此得到闭合曲面净通量表达式: Φ t o t a l = ∂ A x ( x , y , z ) ∂ x △ V + ∂ A y ( x , y , z ) ∂ y △ V + ∂ A z ( x , y , z ) ∂ z △ V Φ_{total} = \frac{\partial A_x(x,y,z)}{\partial x}△V + \frac{\partial A_y(x,y,z)}{\partial y}△V + \frac{\partial A_z(x,y,z)}{\partial z}△V Φtotal=∂x∂Ax(x,y,z)△V+∂y∂Ay(x,y,z)△V+∂z∂Az(x,y,z)△V
把它重新带入散度的定义式,我们就可以得到散度的计算公式: d i v A → = ∂ A x ( x , y , z ) ∂ x + ∂ A y ( x , y , z ) ∂ y + ∂ A z ( x , y , z ) ∂ z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z \begin{aligned} div\overrightarrow{A} &= \frac{\partial A_x(x,y,z)}{\partial x} + \frac{\partial A_y(x,y,z)}{\partial y} + \frac{\partial A_z(x,y,z)}{\partial z}\\ &=\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \end{aligned} divA=∂x∂Ax(x,y,z)+∂y∂Ay(x,y,z)+∂z∂Az(x,y,z)=∂x∂Ax+∂y∂Ay+∂z∂Az
- d i v A → > 0 div\overrightarrow{A} > 0 divA>0:则表示该点处有一个正源(发射矢量线)
- d i v A → < 0 div\overrightarrow{A} < 0 divA<0:则表示该点处有一个负源(吸收矢量线)
- d i v A → = 0 div\overrightarrow{A} = 0 divA=0:则表示该点没有场源
下面我们定义一个以后非常常用的算子: ▽ \triangledown ▽算子:(矢量微分算子) ▽ = ∂ ∂ x a x → + ∂ ∂ y a y → + ∂ ∂ z a z → \triangledown = \frac{\partial }{\partial x}\overrightarrow{a_x} + \frac{\partial}{\partial y}\overrightarrow{a_y} + \frac{\partial }{\partial z}\overrightarrow{a_z} ▽=∂x∂ax+∂y∂ay+∂z∂az
因此,散度就可以表示成: d i v A → = ▽ ⋅ A → div\overrightarrow{A} = \triangledown \sdot \overrightarrow{A} divA=▽⋅A,散度表示矢量场内一点的吸收或者辐射程度
2.3 高斯散度的定理
三、矢量场的旋度
3.1 先从环量说起:
先看看下面的 (a)图,考虑这样一个 A → \overrightarrow{A} A 的矢量场。我们举一个具体的例子:比如说这个一个“风”场,里面每一点的向量的方向代表该点处风力的方向,矢量长度代表该点风力大小。
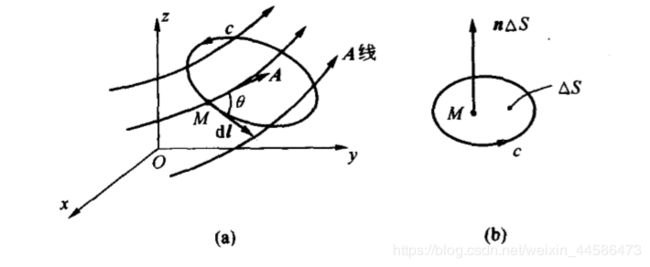
假如这是由龙卷风组成的强大的场,那么试想一下在这个风暴场里面如果有一个飘零的线圈 c c c,我们可以想象得出来,这个线圈将会收到风力的影响而旋转。那么,如何描述这个线圈 c c c 所受到的风力大小呢?
我们先从线圈的一个点开始计算:
假设在线圈上一点 M M M,这个点处线圈的方向是 d l → \overrightarrow{dl} dl,风力场在 M 点的矢量方向是 A → \overrightarrow{A} A,我们知道,只有切线上的力会导致物体旋转,因此,我们也考虑风力在切线方向的作用: A → \overrightarrow{A} A 在 d l → \overrightarrow{dl} dl 方向上的投影恰好就是风力在切线方向的大小。
因此,在这一个点 M 上,所受到的风力大小就是: A → ⋅ d l → \overrightarrow{A}\sdot \overrightarrow{dl} A⋅dl
那么,整个线圈收到的风力大小就是: ∮ c A → ⋅ d l → \oint_c\overrightarrow{A}\sdot \overrightarrow{dl} ∮cA⋅dl
而其实,如果我们假设这个线圈 c c c 内部存在一个涡旋源,我们现在还想研究这个涡旋源的强度:
因此,和推导散度类似的办法,假设线圈的面积是 S,如果令 S 无限趋近于0,就可以缩到如图(b)所示的一个点 M,我们有: lim S → 0 ∮ c A → ⋅ d l → S \lim_{S\to 0}\frac{\oint_c\overrightarrow{A}\sdot \overrightarrow{dl}}{S} S→0limS∮cA⋅dl
这个叫做矢量场 A → \overrightarrow{A} A 在点 M 处沿着方向 n → \overrightarrow{n} n 处的环量面密度。
欸???按照类比的思路,这里的形式不应该是旋量吗?——但是你别忘了,旋量是一个矢量,它还有方向。开始,经过 M 点的平面有无穷多个,那么方向也就是无穷多个。显然不符合旋量的定义。

如图,假设我们的磁场 B → \overrightarrow{B} B 的方向是沿着竖直轴逆时针旋转的,那么经过中心点取的一个平面,假设这个平面和磁场方向平行,那么 B → \overrightarrow{B} B 在该点处沿着该面方向的环量面密度最大。
因此,我们定义环量面密度最大的时候,环量面密度的模值就是旋量的模值,该环线所围的面积的法向就是旋量的方向。记为: r o t A → rot\overrightarrow{A} rotA
公式就直接给出来: r o t A → = ▽ × A → rot\overrightarrow{A} = \triangledown × \overrightarrow{A} rotA=▽×A
即: r o t A → = ▽ × A → = [ a x → a y → a z → ∂ ∂ x ∂ ∂ x ∂ ∂ x A x A y A Z ] rot\overrightarrow{A} = \triangledown × \overrightarrow{A} = \begin{bmatrix} \overrightarrow{a_x} & \overrightarrow{a_y} & \overrightarrow{a_z}\\ \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial x} & \frac{\partial }{\partial x}\\ \\ A_x & A_y & A_Z \end{bmatrix} rotA=▽×A=⎣⎢⎢⎢⎢⎡ax∂x∂Axay∂x∂Ayaz∂x∂AZ⎦⎥⎥⎥⎥⎤
四、梯度、旋度、散度的关系
- 旋度的散度等于0: ▽ ⋅ ( ▽ × A → ) = 0 \triangledown \sdot (\triangledown ×\overrightarrow{A}) = 0 ▽⋅(▽×A)=0
- 梯度的旋度等于0: ▽ × ( ▽ u ) = 0 \triangledown × (\triangledown u) = 0 ▽×(▽u)=0
在这篇 B l o g Blog Blog 的最后,再简单说明一个问题: ▽ \triangledown ▽ 这个算子叫做”矢量微分算子”,也就是说,它既具有矢量的性质,又具有微分的性质(比如复合函数求导法则),我们举两个例子:
【1】 ▽ ( u v ) \triangledown{(uv)} ▽(uv),这时, ▽ \triangledown ▽ 具有微分的性质,我们可以看成是对 u v uv uv 求导,因为 u v uv uv 是一个复合函数,因此就有: u ▽ v + v ▽ u u\triangledown{v} + v\triangledown{u} u▽v+v▽u
【2】因为向量有下面这个性质: A → ⋅ ( B → × C → ) = B → ⋅ ( A → × C → ) = C → ⋅ ( A → × B → ) \overrightarrow{A}\sdot (\overrightarrow{B} × \overrightarrow{C}) = \overrightarrow{B}\sdot (\overrightarrow{A} × \overrightarrow{C}) = \overrightarrow{C}\sdot (\overrightarrow{A} × \overrightarrow{B}) A⋅(B×C)=B⋅(A×C)=C⋅(A×B)
所以, ▽ \triangledown ▽ 也有这样的性质: ▽ ⋅ ( B → × C → ) = B → ⋅ ( ▽ × C → ) = C → ⋅ ( ▽ × B → ) \triangledown\sdot (\overrightarrow{B} × \overrightarrow{C}) = \overrightarrow{B}\sdot (\triangledown × \overrightarrow{C}) = \overrightarrow{C}\sdot (\triangledown × \overrightarrow{B}) ▽⋅(B×C)=B⋅(▽×C)=C⋅(▽×B)
这时我们要把 ▽ \triangledown ▽ 当成矢量看待。