机器学习实战笔记3——K-means聚类
任务安排
1、机器学习导论 8、核方法
2、KNN及其实现 9、稀疏表示
3、K-means聚类 10、高斯混合模型
4、主成分分析 11、嵌入学习
5、线性判别分析 12、强化学习
6、贝叶斯方法 13、PageRank
7、逻辑回归 14、深度学习
K-means聚类
Ⅰ核心思想
如上次介绍的,聚类,是无监督学习
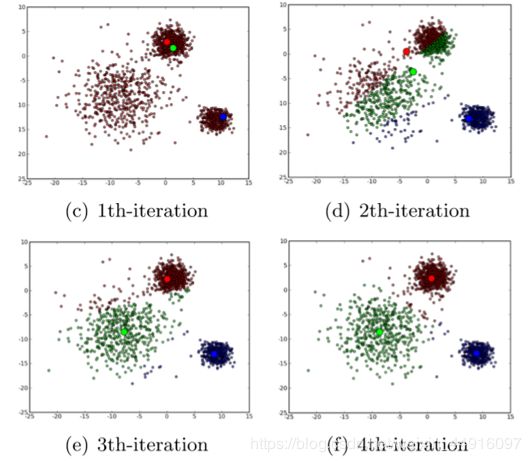
以下图为例:
①首先是随机选取 K 个(即我们想要分成的堆数,这里是 K = 3)对象作为初始的聚类中心
②然后计算每个样本与各个聚类中心之间的距离,把每个样本分配给距离它最近的聚类中心(聚类中心以及分配给它们的对象就代表一个聚类)
③每分配一次样本,聚类的聚类中心会根据聚类中新的样本被重新计算(后面具体讲如何计算)
④这个过程将不断重复直到满足某个终止条件。(终止条件可以是没有(或最小数目)样本被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小)
Ⅱ 算法剖析
输入:数据样本 { x i xi xi} i = 1 n ^n_{i=1} i=1n,聚类个数 K K K,距离函数 d i s t dist dist,终止条件
输出:所有样本的聚类标签 { y i yi yi} i = 1 n ^n_{i=1} i=1n
1.随机生成K个聚类中心, u 1 , … , u k u_1, …, u_k u1,…,uk;
2.计算每个样本与每一个聚类中心的距离(如欧式距离),离哪个聚类中心最近,就划分到那个聚类所属的集合; c l u s t e r i ← a r g ( m i n J ∣ ∣ x i − u j ∣ ∣ ) cluster_i←arg(min_J||x_i-u_j||) clusteri←arg(minJ∣∣xi−uj∣∣)(把样本点的标签记为距离最近的聚类中心的标签)
3、重新计算每个集合的聚类中心; u j = ∑ i = 1 n δ ( c l u s t e r i = j ) x i ∑ i = 1 n δ ( c l u s t e r i = j ) u_j=\frac{∑^n_{i=1}δ(cluster_i=j)x_i}{∑^n_{i=1}δ(cluster_i=j)} uj=∑i=1nδ(clusteri=j)∑i=1nδ(clusteri=j)xi(求均值,如对于聚类中心 u 2 u_2 u2, x 2 x_2 x2 和 x 4 x_4 x4和它同属一类,则重新求的 u 2 = x 2 + x 4 2 u_2=\frac{x_2+x4}{2} u2=2x2+x4)
4、重复 2.&3. 步骤直至达到终止条件;
5、返回所有样本的聚类标签;
★Ⅲ 目标函数
定义目标函数 J = ∑ n = 1 N ∑ k = 1 K r n k ∣ ∣ x n − u k ∣ ∣ 2 J=∑^N_{n=1}∑^K_{k=1}r_{nk}||x_n-u_k||^2 J=n=1∑Nk=1∑Krnk∣∣xn−uk∣∣2其中 r n k r_{nk} rnk 为类别指示函数,当前样本点属于该类则为 1,否则为 0
问题求解: a r g ( m i n J ) arg(min_J) arg(minJ)
u k u_k uk 为目标函数中唯一变量(每一类中 x n x_n xn 作为聚类中心是固定的),令 J J J 对 u k u_k uk 求导得
J ′ = ∑ n = 1 N 2 r n k ( u k − x n ) J'=∑^N_{n=1}2r_{nk}(u_k-x_n) J′=n=1∑N2rnk(uk−xn)令 J = 0 J=0 J=0 得 ∑ n = 1 N r n k u k = ∑ n = 1 N r n k x n ∑^N_{n=1}r_{nk}u_k=∑^N_{n=1}r_{nk}x_{n} ∑n=1Nrnkuk=∑n=1Nrnkxn, 由此可知求解即为求平均值。在每一次聚类的迭代过程中,对该类中所有数据求均值,以更新中心点 u k u_k uk u k = ∑ n = 1 N r n k x n ∑ n = 1 N r n k u_k=\frac{∑^N_{n=1}r_{nk}x_n}{∑^N_{n=1}r_{nk}} uk=∑n=1Nrnk∑n=1Nrnkxn不断重复上述流程直到 u k u_k uk 基本不变,则称收敛,聚类任务完成
Ⅳ 评价指标
不同于 KNN 算法指标一样单一(预测精度),K-means 需要多个指标来评价它的算法性能(以下了解即可)
聚类精度ACC
聚类精度(Clustering accuracy)用于测量实际标签和通过算法获得的预测标签之间的精度。假设一数据集 { x i xi xi} i = 1 n ^n_{i=1} i=1n,实际标签为 g i g_i gi,预测标签为 p i p_i pi,则 ACC 计算公式定义如下:
A C C = ∑ i = 1 n δ ( g i , m a p ( p i ) ) n ACC=\frac{∑^n_{i=1}δ(g_i,map(p_i))}{n} ACC=n∑i=1nδ(gi,map(pi))
m a p ( x ) map(x) map(x)函数是将获得的聚类标签与数据集的等效标签匹配的最佳排列映射函数
标准化互信息NMI
标准化互信息(Normalized mutual imformation)对于给定的两个随机变量 P P P 和 Q Q Q,计算公式如下:
N M I ( P , Q ) = I ( P ; Q ) H ( P ) H ( Q ) NMI(P,Q)=\frac{I(P;Q)}{\sqrt{H(P)H(Q)}} NMI(P,Q)=H(P)H(Q)I(P;Q)
I ( P ; Q ) I(P;Q) I(P;Q)代表P和Q的互信息, H ( P ) H(P) H(P)和 H ( Q ) H(Q) H(Q)分别代表 P P P与 Q Q Q的熵值
调整的兰德系数ARI
A R I = a − b c n ( n − 1 ) / 2 1 2 ( b + c ) − b c n ( n − 1 ) / 2 ARI=\frac{a-\frac{bc}{n(n-1)/2}}{\frac{1}{2}(b+c)-\frac{bc}{n(n-1)/2}} ARI=21(b+c)−n(n−1)/2bca−n(n−1)/2bc
a = ∑ i , j V i j ( V i j − 1 ) 2 , b = ∑ i V i ( V i − 1 ) 2 , c = ∑ j V j ( V j − 1 ) 2 a=∑_{i,j}\frac{V_{ij}(V_{ij}-1)}{2},b=∑_i\frac{V_i(V_i-1)}{2},c=∑_j\frac{V_j(V_j-1)}{2} a=∑i,j2Vij(Vij−1),b=∑i2Vi(Vi−1),c=∑j2Vj(Vj−1), V i j V_{ij} Vij 代表同时在类 i i i,簇 j j j 的样本个数, V i , V j V_i,V_j Vi,Vj 分别代表在类 i i i,簇 j j j 中的样本个数
Ⅴ 优缺点
优点
原理简单,容易解释
代码付现容易
算法速度快,消耗内存小
算法整体效果较好
缺点
需要事先确定超参数 K
对噪声和离群点敏感
结果不一定是全局最优,只能保证局部最优
不能发现非凸形状的簇
分类结果依赖于分类中心的初始化(有可能刚开始的随机聚类中心离所有点都很远,导致没有点分配到与它一类)
今日任务
1. Sklearn 中的 make_circles、make_moons、make_blobs 方法生成数据,用 K-Means 聚类并可视化、求出指标。(指标计算用老师给的库函数)



2.给定的图像,对其像素进行聚类并可视化

任务解决
1、这里用到了新的生成数据函数 make_blobs,其是专门用来生成一堆一堆聚类的分布点
def make_blobs(n_samples=100, n_features=2, centers=None, cluster_std=1.0,
center_box=(-10.0, 10.0), shuffle=True, random_state=None):
# centers = [[, ], [, ]] 可以指定堆数,亦可直接给嵌套列表指定堆数及中心点位置最终画图要标出聚类中心,关键是找到了 KMeans 的一个属性
self.cluster_centers_ = best_centersKMeans 的用法基本和 KNN 差不多,只是一些参数的不同,第一题难度还算友好,直接贴代码
from sklearn.cluster import KMeans
from sklearn.datasets import make_circles, make_moons, make_blobs
import matplotlib.pyplot as plt
from ML_clustering_performance import clusteringMetrics #导入的老师写的库
fig = plt.figure(1)
X1, y1 = make_circles(n_samples=400, factor=0.5, noise=0.1)
plt.subplot(321)
plt.title('original')
plt.scatter(X1[:, 0], X1[:, 1], c=y1)
plt.subplot(322)
plt.title('K-means')
kms = KMeans(n_clusters=2, max_iter=400) # n_cluster聚类中心数 max_iter迭代次数
y1_sample = kms.fit_predict(X1, y1) # 计算并预测样本类别
centroids = kms.cluster_centers_
plt.scatter(X1[:, 0], X1[:, 1], c=y1_sample)
plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='b')
X2, y2 = make_moons(n_samples=400, noise=0.1)
plt.subplot(323)
plt.title('original')
plt.scatter(X2[:, 0], X2[:, 1], c=y2)
plt.subplot(324)
plt.title('K-means')
kms = KMeans(n_clusters=2, max_iter=400)
y2_sample = kms.fit_predict(X2, y2)
centroids = kms.cluster_centers_
plt.scatter(X2[:, 0], X2[:, 1], c=y2_sample)
plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='b')
X3, y3 = make_blobs(n_samples=1000, random_state=9) #
plt.subplot(325)
plt.title('original3')
plt.scatter(X3[:, 0], X3[:, 1], c=y3)
plt.subplot(326)
plt.title('K-means3')
kms = KMeans(n_clusters=3, max_iter=1000)
y3_sample = kms.fit_predict(X3, y3)
centroids = kms.cluster_centers_
# label = kms.labels_
plt.scatter(X3[:, 0], X3[:, 1], c=y3_sample)
plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='b')
print(clusteringMetrics(y1, y1_sample))
print(clusteringMetrics(y2, y2_sample))
print(clusteringMetrics(y3, y3_sample))
# 设置横纵坐标正常显示中文
# plt.rcParams['font.sans-serif'] = ['SimHei']
# plt.rcParams['font.serif'] = ['SimHei']
plt.show()效果图
性能指标(用老师写的库函数,ACC 是写的,NMI 和 ARI 是自带的)
def cluster_acc(y_true, y_pred):
y_true = np.array(y_true).astype(np.int64)
assert y_pred.size == y_true.size
D = max(y_pred.max(), y_true.max()) + 1
w = np.zeros((D, D), dtype=np.int64)
for i in range(y_pred.size):
w[y_pred[i], y_true[i]] += 1
ind = linear_assignment(w.max() - w)
return sum([w[i, j] for i, j in ind]) * 1.0 / y_pred.size
def clusteringMetrics(trueLabel, predictiveLabel):
# Clustering accuracy
ACC = cluster_acc(trueLabel, predictiveLabel)
# Normalized mutual information
NMI = metrics.normalized_mutual_info_score(trueLabel, predictiveLabel)
# Adjusted rand index
ARI = metrics.adjusted_rand_score(trueLabel, predictiveLabel)
return ACC, NMI, ARI
2、代码是借鉴Python计算机视觉:图像聚类
但是因为年代久远,里面用到调整图像大小的函数 imresize 在 SciPy 的版本更新中被淘汰了(1.0以下的还可以用),所以不得不想办法替代,后找到 PIL 里面的替代函数
from PIL import Image
img = np.array(Image.fromarray(myImage).resize((num_px,num_px)))
# codeim = imresize(codeim, im.shape[:2], 'nearest')
codeim = np.array(Image.fromarray(codeim).resize((im.shape[1], im.shape[0])))from scipy.cluster.vq import *
from pylab import *
from PIL import Image
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
# font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14) # 新宋字体 大小14
def clusterpixels(infile, k, steps):
im = array(Image.open(infile))
dx = im.shape[0] / steps
dy = im.shape[1] / steps
# compute color features for each region
features = []
for x in range(steps): # RGB三色通道
for y in range(steps):
R = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 0])
G = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 1])
B = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 2])
features.append([R, G, B])
features = array(features, 'f') # make into array
# 聚类, k是聚类数目
centroids, variance = kmeans(features, k)
code, distance = vq(features, centroids)
# create image with cluster labels
codeim = code.reshape(steps, steps)
# codeim = imresize(codeim, im.shape[:2], 'nearest')
codeim = np.array(Image.fromarray(codeim).resize((im.shape[1], im.shape[0])))
return codeim
# k = 5
infile_MayDay = 'MayDay.png'
im_MayDay = array(Image.open(infile_MayDay))
steps = (50, 100) # image is divided in steps*steps region
# print(steps[0], steps[-1])
# 显示原图MayDay.jpg
figure()
subplot(231)
title('original')
# title(u'原图', fontproperties=font)
axis('off')
imshow(im_MayDay)
# # 用50*50的块对empire.jpg的像素进行聚类
# codeim = clusterpixels(infile_empire, k, steps[0])
# ax1 = subplot(232)
# title(u'k=6,steps=50', fontproperties=font)
# # ax1.set_title('Image')
# axis('off')
# imshow(codeim)
# 用100*100的块对MayDay.jpg的像素进行聚类 效果要比50*50好不少
codeim = clusterpixels(infile_MayDay, 2, steps[-1])
subplot(232)
title('K=2')
# title(u'k=6,steps=100', fontproperties=font)
# ax1.set_title('Image')
axis('off')
imshow(codeim)
codeim = clusterpixels(infile_MayDay, 3, steps[-1])
subplot(233)
title('K=3')
axis('off')
imshow(codeim)
codeim = clusterpixels(infile_MayDay, 4, steps[-1])
subplot(234)
title('K=4')
axis('off')
imshow(codeim)
codeim = clusterpixels(infile_MayDay, 5, steps[-1])
subplot(235)
title('K=5')
axis('off')
imshow(codeim)
codeim = clusterpixels(infile_MayDay, 6, steps[-1])
subplot(236)
title('K=6')
axis('off')
imshow(codeim)
show()