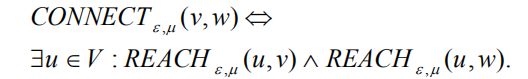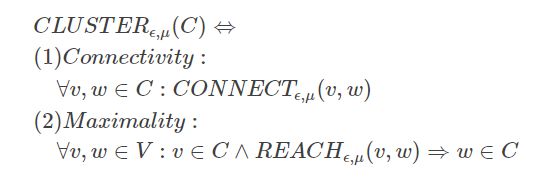【社区发现算法】SCAN: A Structural Clustering Algorithm for Networks

一、论文地址：

https://dl.acm.org/doi/pdf/10.1145/1281192.1281280

发表年份：2007
被引用量：772

二、任务简介：

当前科学界感兴趣的许多数据都可以建模为网络（或图）。网络是顶点的集合，表示对象，通过边连接在一起，表示对象之间的关系。例如，一个社会网络可以被看作是一个图，其中个人由顶点表示，而人与人之间的友谊是边。类似地，万维网可以建模为一个图，其中web页面表示为顶点，当一个页面包含到另一个页面的超链接时，这些顶点就可以通过一条边连接在一起。

而图聚类（或图划分）正是是发现网络底层结构的一项重要任务。许多算法通过最大化集群内边缘的数量来寻找集群。

虽然这些算法可以找到图中一些有用的结构，但它们往往无法识别和分离两种特殊的顶点——桥接集群的顶点（桥节点）和与集群有少量连接的顶点（离群点）。

识别桥节点对于病毒传播和流行病学等应用程序是非常重要的，因为桥节点往往负责传播思想或疾病。相比之下，离群点的影响很小，甚至没有影响，并且可以作为数据中的噪声进行隔离。

三、核心思想：

该文章提出了一种新的图结构聚类算法——SCAN，用于检测网络中的社区、桥节点和离群点。它基于结构相似性度量对顶点进行聚类。该算法特点是：速度快，效率高，每个顶点只访问一次。

主要贡献是能够识别出桥节点和离群点两种特殊点。

四、算法简介：

4.1 传统算法的不足：

网络聚类(或图划分)是检测网络中隐藏结构的一种基本方法，由于许多有趣的应用，在计算机科学、物理和生物信息学中引起了越来越多的关注。

因此人们开发了各种各样的方法。这些方法倾向于群集网络，这样每个群集中都有一组密集的边，而群集之间的边很少。基于模块的和归一化切割算法是典型的例子。

然而，这些算法并不区分网络中顶点的角色。有些顶点是集群的成员；有些顶点是桥接许多集群但不属于任何集群的桥节点，而有些顶点则是只与特定集群有弱关联的离群点。

如下图所示：

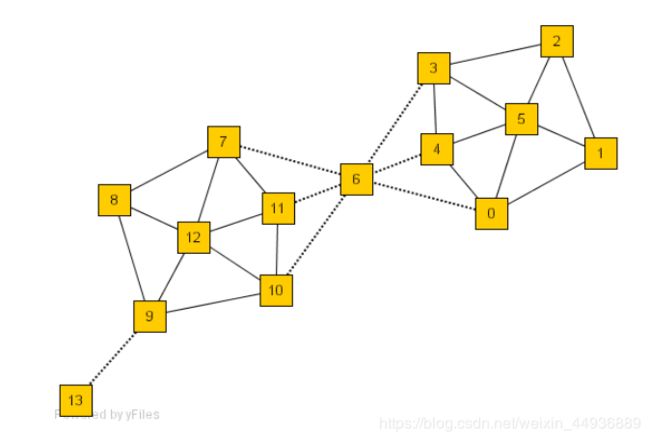
现有的方法，如基于模块的算法，会将这个例子分成两个集群：一个由顶点0到6组成，另一个由顶点7到13组成。它们没有隔离顶点6（一个桥节点，将其划分到在任何一个集群中都是有争议的）或顶点13（一个离群点，它只与网络有一个连接）。

4.2 提出改进目标：

而桥节点和离群点的识别对于许多应用程序来说是至关重要的。

因此这篇文章提出了一种新的网络聚类算法——SCAN（网络结构聚类算法）。该算法的目标是在大型网络中找到集群、桥节点和离群点。

为了实现这个目标，该算法使用顶点的邻域作为聚类标准，而不是只使用它们的直接连接。顶点按照它们共同邻域的方式分组到集群中。

这样做是很有意义的，比如当我们考虑到大型社交网络中的社区检测时，拥有很多共同好友的两个人应该聚集在同一个社区。

再次参考上图中的示例：

1. 考虑顶点 0 和 5，它们由一条边连接。它们的邻域分别是顶点集 {0，1，4，5，6} 和 {0，1，2，3，4，5}。它们共享许多邻居，因此被合理地分组在同一个集群中。
2. 考虑顶点 13 和顶点 9 的邻域。这两个顶点是连接的，但只有两个公共邻居，即 {9,13}。因此，它们是否应该被归为同一类是值得商榷的。
3. 考虑顶点 6 的情况。它有很多邻居，但它们之间的联系很少。

因此通过SCAN最终目标是确定了两个集群，{0，1，2，3，4，5} 和 {7，8，9，10，11，12}，并将顶点 13 作为离群点，将顶点6作为桥节点。

4.3 算法特点：

SCAN 算法有以下特点：

• 通过使用顶点的结构和连接性作为聚类标准来检测集群、桥节点和离群点。理论分析和实验评估证明，SCAN 可以在非常大的网络找到有意义的集群、桥节点和离群点。
• 速度快。它在有n个顶点和m条边的网络上的运行时间是O(m)。

五、一些基础概念：

概算法的目标是优化网络集群，并识别桥节点和离群点。因此，这篇论文在定义最优聚类的同时，使用了连通性和局部结构。本文形式化了结构连接集群的概念，并扩展了基于密度的集群的概念。

现有的网络聚类方法（指的是2007年的时候）的目的是根据顶点之间或集群之间的直接连接边数目来找到最优的网络聚类。直接联系固然很重要，但它们只代表了网络结构的一个方面。

作者认为两个相连点周围的邻域也很重要。一个顶点的邻域包括通过一条边连接到它的所有顶点。当我们考虑一对连接的顶点时，它们的组合邻域显示了两个顶点共有的邻居。因此SCAN算法是基于共同邻域的算法。根据共享邻域的方式，将两个顶点分配给一个集群。

本文主要关注简单的、无向的和未加权的图。

基本图：

设G = {V, E}为一个图，其中V为顶点集合，E是由不同的顶点（无序）组成的集合，称为边。

节点相似度：

节点相似度定义为两个节点共同邻居的数目与两个节点邻居数目的几何平均数的比值（这里的邻居均包含节点自身）。

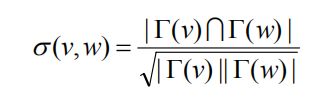
其中 Γ(x) 表示节点 x 及其相邻节点所组成的集合。

ϵ - 邻居：

节点的 ϵ-邻居定义为与其相似度不小于 ϵ 的节点所组成的集合。

核节点：

核节点是指 ϵ-邻居的数目大于 μ 的节点。

直接可达：

节点 w 是核节点 v 的 ϵ-邻居，那么称从 v 直接可达 w。

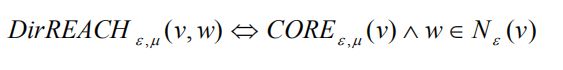
可达：

节点 v 可达 w ，当且仅当存在一个节点链 $v_1,\dots ,v_n\in V,v{1}_{=}v,v_n=w$，使得 $v_{i+1}$ 是从$v_i$直接可达的。

相连：

若核节点u可达节点v和节点w，则称节点v和节点w相连.

相连聚类：

如果一个非空子图C中的所有节点是相连的，并且C是满足可达的最大子图，那么称C是一个相连聚类。

桥节点：

与至少两个聚类相邻的孤立节点。

离群点：

只与一个聚类相邻或不与任何聚类相邻的孤立节点。

引理一：

如果 v 是一个核节点，那么从 v 可达的节点集是一个结构相连聚类。

引理二：

C 是一个结构相连聚类， p 是 C 中的一个核节点。那么 C 等于从 p 结构可达的节点集。

六、算法详解：

6.1 伪代码：

算法SCAN的伪代码如图所示：

SCAN执行一次网络遍历，查找给定参数设置的所有结构连接的集群。

6.2 算法详解：

• 在开始时，所有的顶点都被标记为非分类的。扫描算法对每个顶点进行分类，要么是集群的成员，要么是非成员。
• 对于尚未分类的每个顶点,扫描检查是否这个顶点的核心（STEP 1）。
• 如果顶点是核心，则从这个顶点拓展一个新的集群（STEP 2.1）。否则，顶点标注为非成员（STEP 2.2）。
• 为了找到一个新的集群，从任意核心 v 搜索所有可达顶点。由于引理2，这足以找到包含顶点 v 的完整集群。

在STEP 2.2中，会生成一个新的集群ID，该ID将分配给STEP 2.2中找到的所有顶点。

SCAN首先将顶点 v 的所有其 ϵ-邻居放进队列中。对于队列中的每个顶点，它计算所有直接可达的顶点，并将那些仍未分类的顶点插入队列中。重复此操作，直到队列为空。

6.3 复杂度分析：

对于给定的一个有m条边和n个顶点的图，SCAN首先通过检查图的每个顶点（STEP 1）来查找所有结构连接的群集（需要检索所有顶点的邻居）。图结构使用邻接表存储，其中每个顶点都有一个与之相邻的顶点的列表，邻域查询的成本与邻域的数量成正比，也就是查询顶点的程度。

因此，总代价是$O(deg(v_1)+deg(v_2)+\dots deg(v_n))$，其中$deg(v_i)，i=1,2，\dots ，n$是顶点$v_i$的度。

因此，运行时间为$O(m)$。

如果边的数量未知，还可以根据顶点的数量推导出运行时间。在最坏的情况下，每个顶点连接到一个完整图的所有其他顶点。最坏的情况下，总代价是$O(n(n-1))$或$O(n^2)$。

然而，真实的网络通常具有更稀疏的程度分布。在下面的例子中，作者推导出一个平均情况的复杂度。网络的一种类型是随机图，即通过在顶点之间随机放置边来生成随机图。随机图已被广泛应用于各种类型的现实世界网络的模型，特别是在流行病学中。随机图的度具有泊松分布：

这表明大多数节点具有大致相同数量的链接，即接近$E(k)=z$的平均度。在随机图的情况下，扫描的复杂度为O(n)。

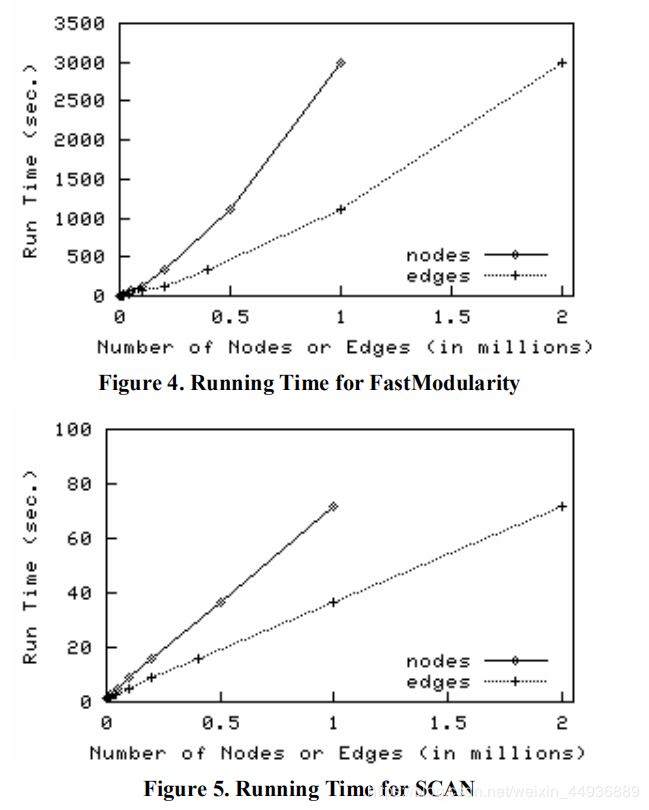
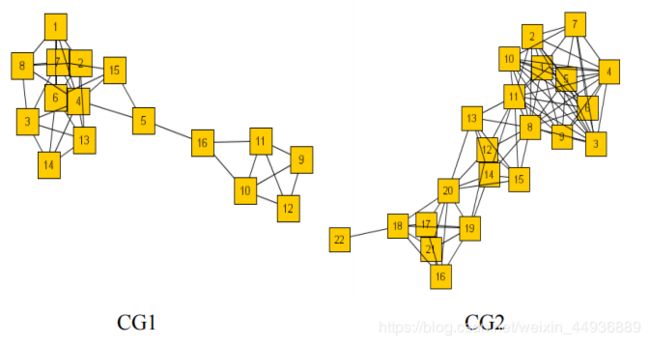
七、算法评估：

作者使用了合成数据集和真实数据集评估算法扫描。

以下为SCAN算法的一些可视化结果：

八、结论：

网络聚类是许多科学和工程领域的一项基本任务。包括计算机科学和物理在内的不同学科的研究者已经提出了许多算法。虽然这种算法可以成功地检测到网络中的集群，但它们往往无法识别和分离两种特殊顶点——桥接集群的顶点（桥节点）和与集群有边缘连接的顶点（离群点）。识别中心对于病毒营销和流行病学等应用至关重要。作为连接集群的顶点，枢纽负责传播思想或疾病。相比之下，异常值的影响很小，甚至没有影响，并且可以作为数据中的噪声进行隔离。

本文提出了一种网络结构聚类算法来检测网络中的集群、桥节点和离群点。扫描基于它们的共同邻居的集群顶点。根据共享邻居的方式，将两个顶点分配给一个集群。