【社区发现/图聚类算法】pSCAN: Fast and exact structural graph clustering
【社区发现/图聚类算法】pSCAN: Fast and exact structural graph clustering
- 未经作者允许,本文禁止转载
- 一、论文地址:
- 二、任务简介:
- 三、SCAN算法:
- 四、PSCAN算法:
- 4.1 摘要:
- 4.2 任务介绍:
- 4.3 现有方法的不足:
- 4.4 本文的贡献:
- 4.5 一些基本概念:
- 4.5.1 定义一:
- 4.5.2 定义二:
- 4.5.3 定义三:
- 4.5.4 定义四:
- 4.5.5 定义五:
- 4.6 SCAN算法分析:
- 4.7 新的范式:
- 4.7.1 观察一:
- 4.7.2 观察二:
- 4.7.3 观察三:
- 4.7.4 范式:
- 集群核心顶点
- 集群非核心顶点
- 算法(伪代码)
- 4.8 pSCAN算法详解:
- 4.8.1 顶点对子集划分:
- 4.8.2 pSCAN算法:
- 4.9 优化技巧:
- 4.9.1 cross link:
- 4.9.2 Pruning Rule:
- 4.9.3 Adaptive Structure-Similar Checking:
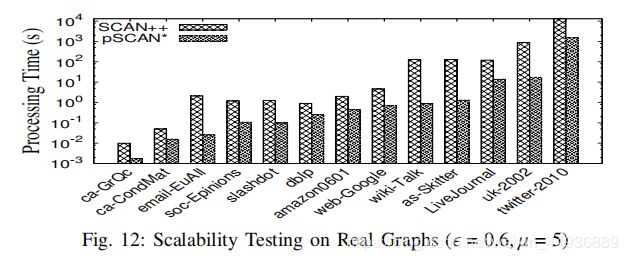
- 4.10 实验结果:
未经作者允许,本文禁止转载
一、论文地址:
https://ieeexplore.ieee.org/abstract/document/7812808/
发表年份:2017
被引用量:51
二、任务简介:
由于图模型强大的表达能力,许多实际应用程序将数据和数据之间的关系建模为图G = (V, E),其中V中的顶点表示感兴趣的实体,E中的边表示实体之间的关系。随着社交网络、信息网络、web搜索、协作网络、电子商务网络、通信网络和生物学等图形应用程序的迅速发展,高效、有效地管理和分析图形数据已经成为研究的重点。其中,图的聚类是一个基本问题,得到了广泛的研究
![]()
而图聚类(或图划分)正是是发现网络底层结构的一项重要任务。许多算法通过最大化集群内边缘的数量来寻找集群。
三、SCAN算法:
详细可以看我这一篇:https://blog.csdn.net/weixin_44936889/article/details/106455436
这里只简单讲一下:
SCAN算法用于检测网络中的社区、桥节点和离群点。它基于结构相似性度量对顶点进行聚类。该算法特点是:速度快,效率高,每个顶点只访问一次。
主要贡献是能够识别出桥节点和离群点两种特殊点。
SCAN 算法有以下特点:
- 通过使用顶点的结构和连接性作为聚类标准来检测集群、桥节点和离群点。理论分析和实验评估证明,SCAN 可以在非常大的网络找到有意义的集群、桥节点和离群点。
- 速度快。它在有n个顶点和m条边的网络上的运行时间是O(m)。
算法SCAN的伪代码如图所示:
![]()
SCAN执行一次网络遍历,查找给定参数设置的所有结构连接的集群。
四、PSCAN算法:
4.1 摘要:
该文章研究了结构化图的聚类问题,这是管理和分析图数据的一个基本问题。
即给定一个图G = (V, E)(可能非常大),结构性图聚类算法会分配顶点V所属的集群,并识别离群点。这篇文章的工作包括:
- 首先,作者证明了现有(指2016年)的SCAN算法方法是最坏情况下最优的。然而,由于要对每一对相邻顶点进行详尽的结构相似性计算,SCAN算法仍然不能扩展到大型图。
- 其次,作者对结构图聚类做了三个观察,为进一步优化提供了机会。
- 基于这些观察,作者提出了一种新的可扩展结构图聚类的两步范式。并在此基础上提出了一种减少结构相似性计算次数的新方法。
- 此外,作者还提出了优化技术来加速检查两个顶点是否结构相似。
- 最后,通过对大型真实和合成图的广泛的性能研究,作者表明新方法比最先进的方法性能好一个数量级。
值得注意的是,对于有10亿条边的twitter图表,该方法只需要25分钟,而最先进的方法甚至在24小时后也无法完成。
4.2 任务介绍:
对于一个较大的图G,图聚类(或图划分)就是对图G中的顶点进行聚类,使得同一簇中的顶点之间有密集的边集,而属于不同簇的顶点之间只有很少的边。
图聚类有很多应用。例如,图聚类可以用于检测图中的隐藏结构。在社交网络(如Facebook)中,图中的集群可以看作是图中的社区。在一个协作网络(例如DBLP)中,集群可能是一组具有相似研究兴趣的研究人员。在计算生物学中,计算基因功能簇可以帮助生物学家进行基因微阵列的研究。
目前已经有学者提出了许多不同的聚类定义,如基于模块化的方法、图划分、基于密度的方法等。但是,所有这些方法都不能区分图中顶点的不同角色;也就是说,一些顶点是集群的成员,而其他的顶点不是,其中一些顶点是连接许多集群的枢纽,而其他的顶点只是离群点。
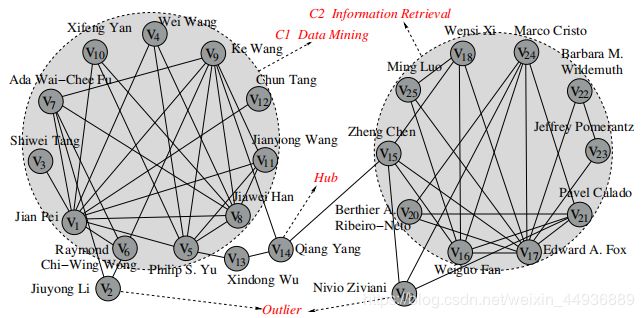
为了区分顶点的不同作用,SCAN算法中提出了结构图聚类。它使用顶点的邻域作为聚类标准,并将顶点u和v之间的结构相似度(u, v)定义为它们的共同邻域的数量。
本文就在此基础上研究结构图聚类的有效计算。
4.3 现有方法的不足:
精确的结构图聚类有两种方法:SCAN和SCAN++。
-
SCAN算法迭代尚未分配给集群的所有顶点。对于每一次这样的顶点u,如果它是一个核心顶点,SCAN算法就会创建一个新的集群(最初只包含u),然后迭代地将所有与顶点u结构相近的顶点添加到C。因此,SCAN算法方法本质上是在计算每一对相邻的顶点的结构相似度。这需要很高的计算成本,并且无法扩展到大型图。
-
SCAN++的设计是基于顶点和它的两步之外(two-hop-away)顶点期望共享其大部分邻域的特性。因此,SCAN++可以避免计算顶点之间的结构相似性,因为这些顶点是顶点的邻居和它的两步之外(two-hop-away)的顶点共享的。与SCAN相比,SCAN++计算的结构相似性较少。然而,SCAN++中结构相似性的计算量仍然很大。
总之,结构化图聚类有两个主要挑战。
- 如何减少结构相似性计算的数量?
- 如何有效地检查两个顶点是否结构相似?
(注意,对于每对未修剪的相邻顶点,所有现有的方法都计算它们的结构相似性的精确值,以确定两个顶点是否彼此结构相似,而这是非常耗时的)
4.4 本文的贡献:
本文证明了现有的SCAN算法在最坏情况下是最优的;然而,由于要对每一对相邻顶点进行详尽的结构相似性计算,它仍然不能扩展到大型图。
为此,本文提出了一种减少结构相似性计算次数和优化两个顶点间结构相似性检查的新方法(也是最坏情况最优的)。
首先,作者对结构图聚类问题做了三个观察:
(1)结构图聚类中的聚类可能存在重叠;
(2)核顶点的集群不相交;
(3)非核心顶点的簇由核心顶点唯一确定。
基于这些观察,作者开发了一个两步的结构图聚类范式。在这个范式中,首先通过将所有核心顶点划分为集群来聚类,然后通过将每个非核心顶点v分配给与其相邻的核心顶点(结构类似于v)相同的集群来聚类非核心顶点。
在此基础上,作者提出了一种基于剪枝(pruned)SCAN的结构图聚类方法,称之为pSCAN:
-
对于每个顶点v∈v,我们递增地维持一个有效度ed(v)和一个相似度sd(v),且ed(v)≥sd(v)。
-
对于顶点v,如果sd(v)≥μ则可判定为核心顶点,如果ed(v) <μ则判定为非核心顶点;以此可以有效地识别核心顶点的集合。
-
然后,根据传递性质计算核心顶点的集群,如果(u, v)∈E,两个核心顶点u和v在同一个集群内,且它们结构相似。
-
此外,如果核心顶点u和v已经被分配到同一个集群中,我们就不再计算它们之间的结构相似性。
因此,pSCAN算法节省了大量的结构相似性计算。
为了提高pSCAN的效率,作者进一步提出了交联、剪枝规则和自适应结构相似检查三种优化技术,在不计算两个顶点结构相似度的情况下,加快了对两个顶点之间结构相似度的检查。
因此该文章的主要贡献概述如下。
- 最坏情况最优性的证明。证明了现有的扫描方法是最坏情况最优的。然而,它仍然不能扩展到大型图形。
- 新的两步范式。基于三个观察结果,作者开发了一个新的两步结构图聚类范例。
- 优化方法。作者提出了一种优化方法,通过减少结构相似性计算的次数和优化两个顶点之间的结构相似性检查。
4.5 一些基本概念:
本文关注一个未加权无向图G = (V, E),其中V是顶点的集合,E是边的集合。顶点的数量表示为|V|,边的数量表示为|E|,在G中分别用n和m代替。令(u, v)∈E表示u和v之间的边,u表示为v的邻居。
为了便于表述,我们简单地将一个未加权无向图称为图。
4.5.1 定义一:
定义顶点 u u u的结构邻域 N [ u ] N[u] N[u]为 u u u的闭邻域,即: N [ u ] = { v ∈ v ∣ ( u , v ) ∈ E } ∪ { u } N[u] = \lbrace v∈v | (u, v)∈E \rbrace∪\lbrace u \rbrace N[u]={v∈v∣(u,v)∈E}∪{u};
在本文中,我们着重于结构邻域(如闭邻域)。而 u u u的度数 d [ u ] d[u] d[u]表示 N [ u ] N[u] N[u]的基数(即 d [ u ] = ∣ N [ u ] ∣ d[u]=|N[u]| d[u]=∣N[u]∣)。注意, u u u的开放邻域记作 N ( u ) N(u) N(u),是 u u u的邻域集合(即 N ( u ) = { v ∈ v ∣ ( u , v ) ∈ E } N(u) = \lbrace v∈v | (u, v)∈E \rbrace N(u)={v∈v∣(u,v)∈E})。
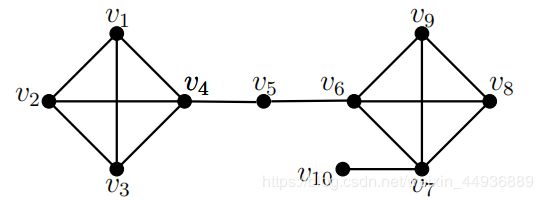
例如下图中的顶点 v 5 v_5 v5,其结构邻域为 N [ v 5 ] = { v 4 , v 5 , v 6 } N[v_5] = \lbrace v_4, v_5, v_6 \rbrace N[v5]={v4,v5,v6},度为 d [ v 5 ] = ∣ N [ v 5 ] ∣ = 3 d[v_5] = |N[v_5]| = 3 d[v5]=∣N[v5]∣=3,开放邻域为 N ( v 5 ) = { v 4 , v 6 } N(v_5) = \lbrace v_4, v_6 \rbrace N(v5)={v4,v6}:
4.5.2 定义二:
顶点 u u u和 v v v之间的结构相似性定义为: N [ u ] N[u] N[u]和 N [ v ] N[v] N[v]中共有顶点的数量按其基数的几何平均值归一化;
也就是说: σ ( u , v ) = ∣ N [ u ] ∩ N [ v ] ∣ d [ u ] ⋅ d [ v ] , 0 ≤ σ ( u , v ) ≤ 1 σ(u, v) = \frac{|N[u] ∩ N[v]|}{\sqrt{d[u] · d[v]}},0≤σ(u, v)≤1 σ(u,v)=d[u]⋅d[v]∣N[u]∩N[v]∣,0≤σ(u,v)≤1
直观上看,对于两个顶点,其结构邻域中的共同顶点越多,结构相似性值越大。
举个例子,在上图中: N [ v 5 ] = { v 4 , v 5 , v 6 } N[v_5] = \lbrace v_4,v_5,v_6 \rbrace N[v5]={v4,v5,v6}和 N [ v 4 ] = { v 1 , v 2 , v 3 , v 4 , v 5 } N [v_4] = \lbrace v_1,v_2,v_3,v_4,v_5\rbrace N[v4]={v1,v2,v3,v4,v5};
因此, σ ( v 4 , v 5 ) = 2 15 σ(v4, v5)=\frac{2}{\sqrt{15}} σ(v4,v5)=152;
给定一个相似度阈值 0 < ϵ ≤ 1 0 <ϵ≤1 0<ϵ≤1, u u u的ϵ-邻居 N ϵ [ u ] N_ϵ[u] Nϵ[u]定义为结构相似度至少为 ϵ ϵ ϵ的 N ( u ) N (u) N(u)的子集,即 N ϵ [ u ] = { v ∈ N [ u ] ∣ σ ( u , v ) ≥ ϵ } N_ϵ[u]= \lbrace v∈N[u]|σ(u, v)≥ϵ \rbrace Nϵ[u]={v∈N[u]∣σ(u,v)≥ϵ}。
例如,在上图中, N 0.8 [ v 4 ] = { v 1 , v 2 , v 3 , v 4 } N_{0.8}[v_4] = \lbrace v_1, v_2, v_3, v_4\rbrace N0.8[v4]={v1,v2,v3,v4}, N 0.8 [ v 7 ] = { v 6 , v 7 , v 8 , v 9 } N_{0.8}[v_7] =\lbrace v_6, v_7, v_8, v_9\rbrace N0.8[v7]={v6,v7,v8,v9}。
4.5.3 定义三:
给定一个相似度阈值 0 < ϵ ≤ 1 0 <ϵ≤1 0<ϵ≤1和一个整数 µ ≥ 2 µ≥2 µ≥2,一个顶点 u u u是核心顶点如果 N ϵ [ u ] ≥ µ N_ϵ[u]≥µ Nϵ[u]≥µ。
如果一个顶点不是核心顶点,那么它就是非核心顶点。例如,给定 ϵ = 0.8 ϵ= 0.8 ϵ=0.8和 µ = 4 µ=4 µ=4,在上图中, v 4 v_4 v4和 v 7 v_7 v7是核心顶点,而 v 5 v_5 v5和 v 10 v_{10} v10非核心顶点。
给定参数 0 < ϵ ≤ 1 0 <ϵ≤1 0<ϵ≤1和 µ ≥ 2 µ≥2 µ≥2,顶点 v v v从顶点 u u u是结构可达的,如果有一个顶点序列 v 1 , v 2 , v l ∈ V v_1,v_2, v_l∈V v1,v2,vl∈V(对于某整数 l ≥ 2 l≥2 l≥2),使得:
- v 1 = u , v l = V v_1 = u, v_l = V v1=u,vl=V;
- v 1 , v 2 , … , v l − 1 v_1,v_2,…,v_{l-1} v1,v2,…,vl−1为核心顶点;
- v i + 1 ∈ N ϵ [ v i ] , 1 ≤ i ≤ l − 1 v_{i + 1}∈N_ϵ[vi],1≤i≤l-1 vi+1∈Nϵ[vi],1≤i≤l−1。
4.5.4 定义四:
集群 C C C是 V V V的一个子集,它至少有两个顶点(即 ∣ C ∣ ≥ 2 |C|≥2 ∣C∣≥2),则:
- (最大化)如果核心顶点 u ∈ C u∈C u∈C,那么所有从 u u u到结构可达的顶点也属于 C C C。
- (连通性)对于任意两个顶点 v 1 , v 2 ∈ C v_1, v_2∈C v1,v2∈C,有顶点 u ∈ C u∈C u∈C,使得 v 1 v_1 v1和 v 2 v_2 v2都可以从 u u u可达。
例如,给定 ϵ = 0.8 , µ = 4 ϵ= 0.8,µ= 4 ϵ=0.8,µ=4,上图中有两个集群: C 1 = { v 1 , v 2 , v 3 , v 4 } C_1 = \lbrace v_1,v_2,v_3,v_4\rbrace C1={v1,v2,v3,v4}和 C 2 = { v 6 , v 7 , v 8 , v 9 } C_2 = \lbrace v_6,v_7,v_8,v_9\rbrace C2={v6,v7,v8,v9}。
那么给定一个图 G = ( V , E ) G = (V, E) G=(V,E)和参数 0 < ϵ ≤ 1 0 <ϵ≤1 0<ϵ≤1和 µ ≥ 2 µ≥2 µ≥2,在本文中,我们研究的问题就是如何有效地计算集群组 C C C。
4.5.5 定义五:
图 G G G中的桥顶点和离群点定义如下:
给定图 G G G中集群的集合 C C C, C C C中不属于任何集群的顶点 u u u,如果它的邻居属于两个或两个以上集群,则为桥顶点,否则为离群点。
例如,给定 ϵ = 0.8 , µ = 4 ϵ= 0.8,µ= 4 ϵ=0.8,µ=4,在图中 C = { { v 1 、 v 2 、 v 3 v 4 } , { v 6 , v 7 , v 8 , v 9 } } C = \lbrace \lbrace v_1、v_2、v_3 v_4 \rbrace, \lbrace v_6, v_7, v_8, v_9 \rbrace \rbrace C={{v1、v2、v3v4},{v6,v7,v8,v9}}, v 5 v_5 v5为桥顶点,因为邻居 v 4 v_4 v4和 v 6 v_6 v6属于不同的集群, v 10 v_{10} v10是离群点,因为它只有一个邻居。
4.6 SCAN算法分析:
伪代码:

由于扫描是最坏情况最优,因此不可能有一种最坏情况时间复杂度优于SCAN的结构图聚类算法。
4.7 新的范式:
4.7.1 观察一:
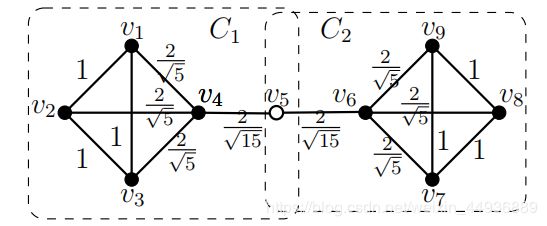
通过结构图聚类计算得到的聚类可能存在重叠。
例如,考虑 ϵ = 2 15 , µ = 4 ϵ=\frac{2}{\sqrt{15}},µ= 4 ϵ=152,µ=4,相邻顶点的结构相似性如边上所示。
可以验证,所有边 ( u , v ) (u, v) (u,v)都有 σ ( u , v ) ≥ ϵ σ(u, v)≥ϵ σ(u,v)≥ϵ的图,并且除了 v 5 v_5 v5的所有顶点都是核心顶点。因此,图中的图有两个集群, C 1 = { v 1 , … , v 5 } C_1 = \lbrace v_1,…, v_5\rbrace C1={v1,…,v5}和 C 2 = { v 5 , … , v 9 } C_2 = \lbrace v_5,…, v_9\rbrace C2={v5,…,v9},其中 v 5 v_5 v5属于两个集群。
因此,将图划分为不相交的子图将不能在图中生成正确的集群。
4.7.2 观察二:
核心顶点的集群是不相交的。
虽然集群可能重叠,但是我们可以证明每个核心顶点属于一个唯一的集群;
4.7.3 观察三:
非核心顶点的集群是由核心顶点唯一确定的。
考虑 G G G核心顶点的集群 C c C_c Cc,非核心顶点可以分配到集群 C i ∈ C c C_i∈C_c Ci∈Cc,如果存在核心顶点 u ∈ C i u∈C_i u∈Ci并且 v ∈ N ϵ [ u ] v∈N_ϵ[u] v∈Nϵ[u]。
例如,在图中非核心顶点 v 5 v_5 v5可以分配给两个集群,因为 v 5 ∈ N ϵ [ v 4 ] v_5∈N_ϵ[v_4] v5∈Nϵ[v4]并且 v 5 ∈ N ϵ [ v 6 ] v_5∈N_ϵ[v_6] v5∈Nϵ[v6]。
假设C_c为G中的核心顶点集群集和。那么集群中的所有顶点集 G G G是 C = { C i ∪ u ∈ C i N ϵ ( u ) ∣ C i ∈ C c } C = \lbrace C_i \cup_{u∈C_i}N_ϵ(u) | C_i∈C_c\rbrace C={Ci∪u∈CiNϵ(u)∣Ci∈Cc}。
4.7.4 范式:
基于以上三个观察结果,作者开发了一种新的结构图聚类范式,该范式包括两个步骤:
- 聚类核心顶点;
- 集群非核心顶点。
集群核心顶点
为了有效地聚类核心顶点,作者提出了连通图的概念。
给定一个图 G = ( V , E ) G = (V, E) G=(V,E),定义一个连接图 G c = ( V c , E c ) G_c = (V_c,E_c) Gc=(Vc,Ec),其中 V c V_c Vc是 G G G的核心顶点集,并且边 ( u , v ) ∈ E c (u, v)∈E_c (u,v)∈Ec当且仅当 u , v ∈ V c u, v∈V_c u,v∈Vc且 ( u , v ) ∈ E (u, v)∈E (u,v)∈E且 σ ( u , v ) ≥ ϵ σ(u, v)≥ϵ σ(u,v)≥ϵ。
在下面的引理中,作者证明了 G G G中的核心顶点集群与 G c G_c Gc中的连通部分之间存在一一对应关系,其中连通部分是任意两个顶点通过一条路径相互连接的最大子图。
对于 G G G中的任意两个核顶点 u u u和 v v v,它们在 G G G中的同一集群中,当且仅当它们在 G c G_c Gc中的同一连通部分。
集群非核心顶点
非核顶点的集群可以直接按照观察三计算。
算法(伪代码)
在以上引理的基础上,下述算法给出了结构图两步聚类范式的伪代码,该算法首先计算核心顶点的集群,然后将非核心顶点分配给集群(注意,为了简单表示,在下述算法中假设连通性图 G c G_c Gc包含了 G G G中的所有顶点;不过,作为后处理,可以从 G c G_c Gc中删除非核心顶点);
在下述算法中,第1-8行聚类核顶点,第9行聚类非核顶点。
- 为了聚类核顶点,我们根据引理构造连通图 G c G_c Gc。
- 对于每一个顶点 u ∈ V u ∈ V u∈V,我们首先确定 u u u是否是一个 核心顶点(第4行)。
- 如果 u u u是一个核心顶点(第5行),则对每个核心顶点,若 v ∈ N ϵ [ u ] v∈N_ϵ[u] v∈Nϵ[u](第6行),则在 G c G_c Gc中添加一个边(u, v)(第7行),然后每组核心顶点在 G c G_c Gc是一 G G G中的核心顶点集群(第8行)。
- 最后,非核心顶点根据引理被添加到集群(第9行)。
4.8 pSCAN算法详解:
基于上述观察和新范例,在本节中,我们将介绍结构图聚类的新方法——pCSAN。
4.8.1 顶点对子集划分:
该算法的目标是减少结构相似性计算的次数。因此,我们将所有相邻的顶点对(即 E E E)分成三个子集 E n , n E_{n,n} En,n, E c , c E_{c,c} Ec,c和 E c , n E_{c,n} Ec,n,分别讨论如何减少每个子集内的计算次数。
其中, E n , n E_{n,n} En,n是相邻的非核心顶点对的集合, E c , c E_{c,c} Ec,c是相邻的核心顶点对的集合, E c , n E_{c,n} Ec,n是核心顶点和非核心顶点之间的相邻顶点对的集合。
4.8.2 pSCAN算法:
遵循算法2的一般范式,我们提出了一种剪枝SCAN算法,简称pSCAN,用于结构图聚类。算法3给出了pSCAN的伪代码。
- 对于每个顶点 u ∈ V u∈V u∈V,我们首先计算两个值(第2-4行),它们的定义将在稍后讨论;
- 然后,我们迭代检查每个顶点 u ∈ V u∈V u∈V是否为核顶点(第6行);如果 u u u是一个核心顶点,那么我们将它的那些被确定为核心顶点的邻居聚在一起(第7行);
- 从分离集数据结构中生成核顶点集群的集合 C c C_c Cc(第8行),最后对非核顶点进行聚类(第9行)。
在算法3中,我们使用一个分离集数据结构(a disjoint-set data structure)来增量地维护 G c G_c Gc中连接的组件,而不是显式地构造连接图 G c G_c Gc。该数据结构维护了不相交动态子集的集合 S = { s 1 , s 2 , . . . } S = \lbrace s1, s2,...\rbrace S={s1,s2,...},并具有查找子集和并集两个基本操作。
查找子集(find-subset):
确定特定元素在哪个子集中,并将两个子集连接为单个子集。最初, G G G中的每个顶点形成了一个单元素子集(第1行),通过 u n i o n ( u , v ) union(u, v) union(u,v)在 G c G_c Gc中添加一条边 ( u , v ) (u, v) (u,v)。
因此两个顶点 u u u和 v v v属于同一连接组,当且仅当他们所属数据结构的同一个子集(即, f i n d − s u b s e t ( u ) = f i n d − s u b s e t ( v ) find-subset(u) =find-subset(v) find−subset(u)=find−subset(v))。
顶点探索顺序(Vertex Exploration Order):
为了减少结构相似性计算的数量,我们以**有效度(effective-degrees)**不增加的顺序(第5行)探索 G G G中的顶点,其定义如下:顶点 u ∈ V u∈V u∈V的有效度,记作 e d ( u ) ed(u) ed(u),是 u u u的度减去已确定与 u u u结构不相似的 u u u的邻居的数量。
凭直觉,,顶点u的有效度就是ϵ-邻居的规模上限(即 ∣ N ϵ [ u ] ∣ ≤ e d ( u ) |N_ϵ[u] |≤ed (u) ∣Nϵ[u]∣≤ed(u))。因此,顶点的有效度越大,越有可能是核顶点。
例如,在图中,假设 σ ( v 4 , v 6 ) < ϵ σ(v4, v6) <ϵ σ(v4,v6)<ϵ且 σ ( v 1 , v 6 ) < ϵ σ(v1, v6) <ϵ σ(v1,v6)<ϵ,那么 e d ( v 6 ) = d [ v 6 ] − 2 = 2 ed (v6) = d [v_6] - 2 = 2 ed(v6)=d[v6]−2=2。
优先探索更可能是核心顶点的顶点的合理性如下:
在获得一组核心顶点的集合KaTeX parse error: Expected group after '_' at position 3: Vc_̲并计算结构核心顶点之间的相似之处和他们的邻居之后,我们可以正确地生成集群而无需计算其他顶点对的计算结构相似度。这样,我们减少了在 E n , n E_{n,n} En,n中顶点对结构相似度计算的次数。
例如,在图5中,假设 { v 1 , … , v 5 } \lbrace v_1,…,v_5 \rbrace {v1,…,v5}为核心顶点的集合,则无需计算 v 6 v_6 v6和 v 7 v_7 v7之间的结构相似性来计算图中的集群。
(注意,当一个顶点 u u u的更多邻居被探索并确定为非结构相似时,它的有效度就会降低)
检查核心顶点(Checking Core Vertices.):
为了有效地检查一个顶点是否为核心顶点,我们计算每个顶点 u ∈ V u∈V u∈V的相似度,定义如下:顶点 u ∈ V u∈V u∈V的相似度,记为 s d ( u ) sd(u) sd(u),是已经确定 u u u与 u u u结构相似的邻居的数量。
直观地,顶点 u u u的相似度ϵ-邻居规模下限(即 ∣ N ϵ [ u ] ∣ ≥ s d ( u ) |N_ϵ[u] | ≥sd (u) ∣Nϵ[u]∣≥sd(u));因此,当 s d ( u ) ≥ μ sd(u)≥μ sd(u)≥μ时,无需探索 u u u即可确定 u u u为核心顶点。
例如,在图5中,假设 v 1 , … , , v 5 v_1,…,,v_5 v1,…,,v5结构相似,且 v 1 、 v 3 、 v 4 v_1、v_3、v_4 v1、v3、v4已经被探索过,那么 s d ( v 2 ) = s d ( v 5 ) = 4 sd(v_2) = sd(v_5) = 4 sd(v2)=sd(v5)=4;如果 μ ≤ 4 μ≤4 μ≤4,那么我们可以确定 v 2 v_2 v2和 v 5 v_5 v5是核心顶点,而不需要对它们进行探索。

基于顶点的相似度,检验顶点 u u u是否是核顶点的伪代码如算法4所示。
- 如果 e d ( u ) < μ ed(u) <μ ed(u)<μ,则 u u u不是核心顶点;如果 s d ( u ) ≥ μ sd(u)≥μ sd(u)≥μ,则 u u u是核心顶点。注意 e d ( u ) ≥ s d ( u ) ed(u)≥sd(u) ed(u)≥sd(u)。
- 如果 e d ( u ) ≥ p a i n l e > s d ( u ) ed(u)≥painle> sd(u) ed(u)≥painle>sd(u)(第1行),我们需要计算 u u u与其相邻节点的结构相似性来确定 u u u是否为核心顶点。
- 然后重新初始化 e d ( u ) ed(u) ed(u)和 s d ( u ) sd(u) sd(u)(第2行)。
- 对于每个顶点 v ∈ N [ u ] v∈N[u] v∈N[u],首先计算 u u u和 v v v的结构相似度(第4行),并相应地更新 s d ( u ) sd(u) sd(u)或 e d ( u ) ed(u) ed(u)(第5-6行)。也就是说,如果 σ ( u , v ) ≥ ϵ σ(u, v)≥ϵ σ(u,v)≥ϵ,就增加 s d ( u ) sd(u) sd(u),否则,我们减少 e d ( u ) ed(u) ed(u)。
- 计算完 σ ( u , v ) σ(u, v) σ(u,v)后,如果 v v v还没有被探索,我们还会更新 s d ( v ) sd(v) sd(v)或 e d ( v ) ed(v) ed(v)(第7-9行)。
- 而且,一旦 e d ( u ) < μ ed(u) <μ ed(u)<μ(即 u u u为非核心顶点)或 s d ( u ) ≥ μ sd(u)≥μ sd(u)≥μ(即 u u u是核心顶点),算法提前终止(第10行)。
注意,在第8-9行,我们还更新了未探索顶点的有效度和相似度。因此,通过这种方式,顶点 v v v可以被确定为一个核心顶点或一个非核心顶点而无需被探索。
集群核心顶点(Clustering Core Vertices):
算法5给出了聚类核心顶点的邻居(也是核心顶点)的伪代码。
- 我们首先将与 u u u结构类似的核心顶点(同时也是 u u u的邻居顶点)分配到与 u u u相同的集群中(第1-3行)。
- 然后,对于每个尚未被计算的 u u u的结构相似邻居 v v v,如果 u u u和 v v v尚未分配给相同的集群(第5行),那么我们计算 σ ( u , v ) σ(u, v) σ(u,v)(第6行),并更新 s d ( v ) sd (v) sd(v)或者 e d ( v ) ed (v) ed(v)(如果 v v v没有被探索)(7 - 9行)。
- 此外,如果 v v v也被确定为核心顶点,并且结构相近与 u u u(第10行),我们将 u u u和 v v v分配到同一个集群中。
通过第5行,我们减少了 E c , c E_{c,c} Ec,c中顶点对结构相似度计算的数量。
集群非核心顶点(Clustering Core Vertices):
G G G的非核心顶点被分配到集群 C = { C i ∪ u ∈ C i N ϵ ( u ) ∣ C i ∈ C c } C = \lbrace C_i \cup_{u∈C_i}N_ϵ(u) | C_i∈C_c\rbrace C={Ci∪u∈CiNϵ(u)∣Ci∈Cc}。
伪代码如算法6所示。
对于每个 u ∈ C c u∈C_c u∈Cc,我们将 N ϵ [ u ] N_ϵ[u] Nϵ[u]中的所有顶点放到相同的集群作为 C c C_c Cc。为此,我们将遍历 u u u的每个邻居 v v v(即 v ∈ N [ u ] v∈N[u] v∈N[u]),并检查 u u u与 v v v是否结构相似。
注意,这里只有在 v v v是一个非核心顶点并且 v v v没有分配给相同的集群 C c C_c Cc的情况下,我们才会计算 σ ( u , v ) σ(u, v) σ(u,v)。原因在于,如果 v v v也是一个核心的顶点,然后 u u u和 v v v是否属于同一集群已经被计算过了。
这样,我们减少了 E c , n E_{c,n} Ec,n中顶点对结构相似度计算的次数。
以非递增有效度顺序访问顶点(Accessing Vertices in Non-increasing Effective-degree Order):
在算法3的第5行,我们以非递增有效度顺序访问顶点,一个顶点的有效度会动态更新。因此,我们需要一个数据结构来反复检索元素最高元素动态更新的键值。斐波那契堆可以支持这些操作,但是它的时间复杂度仍然太高,而且数据结构过于复杂,难以实现。
基于有效度是1到n范围内的整数这一事实,作者提出了一种bin-sort数据结构。在该数据结构中,我们有n个bins,每个bin对应不同的有效度值。bin i i i由一个双链表组成,将有效度为 i i i的顶点集合连接在一起。
因此,更新一个顶点的有效度可以在 O ( 1 ) O(1) O(1)时间内完成,方法是将其从一个双链表中移除,并将其添加到另一个双链表中。通过保持剩余顶点的最大有效度,可以在 O ( n ) O(n) O(n)时间内完成检索效率最大顶点的n次操作,且非递增。
因此,与该数据结构相关的总时间复杂度为 O ( m ) O(m) O(m)。此外,我们对数据结构中顶点的有效度进行惰性更新(只有当它被选择为下一个有效度最大的顶点时才会被更新)。因此,单链表就足够了。
计算结构相似度:
要计算顶点 u u u和 v v v之间的结构相似性,首先需要计算 N [ u ] ∩ N [ v ] N[u]∩N[v] N[u]∩N[v],然后可以在 O ( ∣ N [ u ] ∩ N [ v ] ∣ ) O(|N[u]∩N[v]|) O(∣N[u]∩N[v]∣)时间内完成计算 σ ( u , v ) σ(u, v) σ(u,v)。如果我们创建一个哈希结构来存储 E E E中的所有边,则 N [ u ] ∩ N [ v ] N[u]∩N[v] N[u]∩N[v]可以在 O ( m i n d [ u ] , d [ v ] ) O(min{d[u], d[v]}) O(mind[u],d[v])时间内计算。
例如,假设 d [ u ] ≤ d [ v ] d[u]≤d[v] d[u]≤d[v],那么对于每个 w ∈ N [ u ] w∈N[u] w∈N[u], w w w在 N [ v ] N[v] N[v]中当且仅当 ( v , w ) (v,w) (v,w)在可在常量时间内测试的哈希结构中。因此, E s E_s Es中所有相邻顶点对的结构相似性计算的总时间复杂度为 O ( Σ ( u , v ) ∈ E s m i n { d [ u ] , d [ v ] } ) O(Σ_{(u,v)∈E_s}min\lbrace d[u],d[v]\rbrace) O(Σ(u,v)∈Esmin{d[u],d[v]})。
但是,构建哈希结构会带来额外的时间和空间,这可能是一个很大的开销。因此,作者考虑另一种方法。即假设输入图以邻接表的形式存储(每个邻接表用数组表示),每个邻接表中的顶点按id递增;即对于每个顶点 v ∈ v v∈v v∈v, N [ v ] N[v] N[v]是一个排序列表。那么, N [ u ] ∩ N [ v ] N[u]∩N[v] N[u]∩N[v]可以通过交叉 N [ u ] N[u] N[u]和 N [ v ] N[v] N[v]进行计算,可以在 O ( d [ u ] + d [ v ] ) O(d[u] + d[v]) O(d[u]+d[v])时间中以排序合并连接方式完成。
(虽然理论上这不如上面的哈希结构实现,但作者的实验证明,这种方法在实践中性能更好)
4.9 优化技巧:
在本节中,为了加速检查两个顶点之间的结构相似性(即是否有 σ ( u , v ) ≥ ϵ σ(u, v)≥ϵ σ(u,v)≥ϵ),作者提出可三个优化技术:cross link、Pruning Rule和自适应结构相似检查。
4.9.1 cross link:
在算法3中,对顶点 u u u和 v v v的结构相似性计算两次:一个在探索 u u u时计算的 σ ( u , v ) σ(u, v) σ(u,v)和另一个在探索 v v v时计算的 σ ( u , v ) σ(u, v) σ(u,v)。因此,如果我们联系边 ( u , v ) (u, v) (u,v)和边 ( v , u ) (v, u) (v,u),那么我们只需要计算 u u u和 v v v的结构相似性一次,就可以分配两个 σ ( u , v ) σ(u, v) σ(u,v)和 σ ( v , u ) σ(v, u) σ(v,u)。
因此作者建议建立一个交叉链接的每条边连接两个方向相同的优势,基于结构相似度计算的总数预计将减少一半。由于每个邻接表 N [ u ] N[u] N[u]都是一个顶点id有序表,对于一条边 ( u , v ) (u, v) (u,v),通过对 N [ v ] N[v] N[v]进行二分搜索,可以在 N [ v ] N[v] N[v]中找到它的反边 ( v , u ) (v, u) (v,u),时间复杂度为 l o g d [ v ] log d[v] logd[v]。因此,cross link的总时间复杂度为 O ( Σ ( u , v ) ∈ E m i n l o g d [ u ] , l o g d [ v ] ) O(Σ_{(u,v)∈E} min{log d[u], log d[v]}) O(Σ(u,v)∈Eminlogd[u],logd[v])。
4.9.2 Pruning Rule:
在算法3中,不需要计算顶点 u u u和 v v v之间确切的结构相似性,只需要确定 u u u和 v v v是否具有结构相似性就足够了。因此,作者在下面的引理中提出了一个Pruning Rule,以有效地确定 u u u和 v v v在结构上不相似( σ ( u , v ) < ϵ σ(u, v) <ϵ σ(u,v)<ϵ)。
对于顶点 u u u和 v v v,如果 d [ u ] < ϵ 2 ⋅ d [ v ] d[u]<ϵ^2·d [v] d[u]<ϵ2⋅d[v]或 d [ v ] < ϵ 2 ⋅ d [ u ] d[v]<ϵ^2·d [u] d[v]<ϵ2⋅d[u],那么 σ ( u , v ) < ϵ σ(u, v) <ϵ σ(u,v)<ϵ。
Pruning Rule的伪代码如算法7所示。对于每条边 ( u , v ) ∈ E (u, v)∈E (u,v)∈E(第1-2行),我们首先应用引理中的修剪规则。如果修剪 ( u , v ) (u, v) (u,v)(第3行),我们给 σ ( u , v ) σ(u, v) σ(u,v)分配任意小于ϵ的值(例如,0)(第4行),并减少 u u u的有效度(第5行)。否则,我们在边 ( u , v ) (u, v) (u,v)和边 ( v , u ) (v, u) (v,u)之间建立交叉链接。
其中时间复杂度为: O ( Σ ( u , v ) ∈ E m i n l o g d [ u ] , l o g d [ v ] ) O(Σ_{(u,v)∈E} min{log d[u], log d[v]}) O(Σ(u,v)∈Eminlogd[u],logd[v])。
4.9.3 Adaptive Structure-Similar Checking:
作者提出了一种自适应的方法,在检测两个顶点之间的结构相似性时,无需计算精确的结构相似性就可以提前终止。首先,在下面的引理中,我们计算 u u u和 v v v之间的最小共同邻居数,记作 c n ( u , v ) cn(u, v) cn(u,v),它是 u u u和 v v v在结构上相似所必需的。
假设 c n ( u , v ) cn (u, v) cn(u,v)为不少于 ϵ ⋅ d [ u ] ⋅ d [ v ] ϵ·\sqrt{d [u]·d [v]} ϵ⋅d[u]⋅d[v]最小的整数。那么 σ ( u , v ) ≥ ϵ σ(u, v) ≥ϵ σ(u,v)≥ϵ当且仅当 ∣ N [ u ] ∩ N [ v ] ∣ ≥ c n ( u , v ) | N [u]∩N [v] |≥cn (u, v) ∣N[u]∩N[v]∣≥cn(u,v)。
这里,我们假设 N [ u ] ∩ N [ v ] N[u]∩N[v] N[u]∩N[v]是以排序-合并连接样式计算的。一旦 c n ≥ c n ( u , v ) cn≥cn(u, v) cn≥cn(u,v)或 d u < c n ( u , v ) d_u < cn (u, v) du<cn(u,v)或 d v < c n ( u , v ) d_v < cn (u, v) dv<cn(u,v),我们提前终止算法。
算法8与的时间复杂度为 O ( d [ u ] + d [ v ] ) O(d[u] + d[v]) O(d[u]+d[v])。