机器学习-梯度下降法(SGD+BGD+MBGD)
SGD:随机梯度下降在每次更新的时候,只考虑了一个样本点,这样会大大加快训练数据,也恰好是批梯度下降的缺点,因为不一定每次都朝着梯度下降的方向。
BGD:批量梯度下降每次更新都使用了所有的样本数据,朝着最小值迭代运动的,缺点就是速度很慢。
MBGD:综合批量梯度下降法和随机梯度下降法的优点。
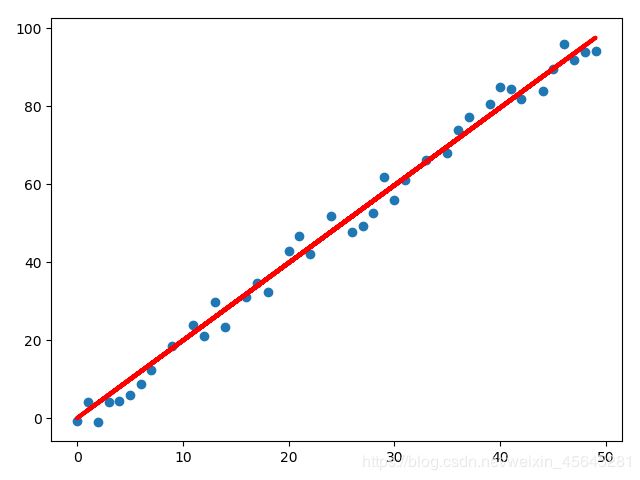
线性回归
这里只是测试了一元线性回归,还有多元线性回归。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
##### 产生数据集 #####
x = np.arange(0,50)
np.random.seed(1)
#添加50个随机噪声,范围[-5,5]
random_array=(np.random.random(50)*2-1)*5
y = 2 * x + random_array
#转换二维数组
x=x.reshape(50,1)
y=y.reshape(50,1)
data=np.concatenate((x,y),axis=1)
plt.scatter(x,y)
plt.show()
def ML():
##### 机器学习模块调用 #####
# 训练模型
lr = LinearRegression()
lr.fit(x, y)
# 绘制数据散点图和拟合直线
plt.scatter(x, y)
plt.plot(x, lr.predict(x), color='red', linewidth=3)
plt.show()
def SGD():
NUM=1 #标记
N = 1000 #最大循环次数
epsilon = 190 #误差阈值
theta = np.random.rand() # 线性模型的系数
learning_rate = 0.001 # 学习率
#x = np.hstack([np.ones((50,1)),x]) # 增加全1列
np.random.shuffle(data)
#训练集与测试集
train_data=data[:40]
test_data=data[40:]
#存放数据列表
theta_list=[]
loss_list=[]
while True:
np.random.shuffle(train_data)
for n in range(N):
#取随机样本
randint = np.random.randint(0,40)
temp_x = train_data[randint][0]
temp_y = train_data[randint][1]
#计算梯度
grad = temp_x * (temp_x * theta - temp_y)
theta = theta - learning_rate*grad
x=train_data[:,0]
y=train_data[:,1]
loss=np.sum(0.5*(theta*x-y)**2)
theta_list.append(theta)
loss_list.append(loss)
NUM=NUM+1
print("num: %d ,theta: %s ,loss: %s "%(NUM,theta,loss))
if loss<epsilon:
break
plt.scatter(x,y)
plt.plot(x,x*theta,color='red',linewidth=3)
plt.show()
def BGD():
NUM = 1 # 标记
N = 100 # 最大循环次数
theta = np.random.rand() # 线性模型的系数
learning_rate = 0.001 # 学习率
for i in range(N):
pred_y = np.dot(x,theta)
loss = pred_y - y
# 计算梯度
grad = np.dot(x.T,loss)/x.shape[0]
# 更新theta
theta = theta - learning_rate*grad
sum_loss=np.sum(pred_y - y)
NUM = NUM + 1
# 输出当前的更新次数和误差
print("num: %d ,theta: %s ,sum_loss: %s " % (NUM, theta, sum_loss))
# 绘制拟合的曲线
plt.scatter(x,y)
plt.plot(x,x*theta,color='green',linewidth=3)
plt.show()
def MBGD():
N = 200 # 最大循环次数
theta = np.random.rand() # 线性模型的系数
learning_rate = 0.001 # 学习率
epsilon = 20 # 误差阈值
# 还原参数theta,其他参数复用梯度下降
#theta = np.random.rand(2,1)
# 指定每次更新使用的数据量
batch_size = 20
for i in range(N):
# 随机样本的列索引
indexs = np.random.randint(0, x.shape[0], size=batch_size)
# 随机样本
temp_x = x.take(indexs, axis=0)
temp_y = y.take(indexs, axis=0)
# 计算梯度
grad = np.dot(temp_x.T, (np.dot(temp_x, theta) - temp_y)) / temp_x.shape[0]
# 更新theta
theta = theta - learning_rate * grad
# 计算更新后的误差
error = np.linalg.norm(np.dot(x, theta) - y)
# 输出当前的更新次数和误差
print("number is %d. error is %f"%(i,error))
# 误差小于阈值时退出循环
print("thema: %s"%(theta))
if error < epsilon:
break
# 绘制拟合的曲线
plt.scatter(x, y)
plt.plot(x, np.dot(x, theta), color='red', linewidth=3)
plt.show()
if __name__=="__main__":
#SGD()
#BGD()
MBGD()
结果:
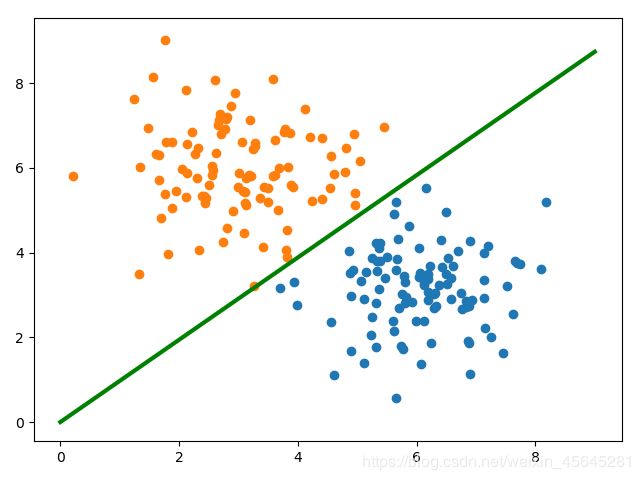
逻辑回归
原始数据集:
import numpy as np
import matplotlib.pyplot as plt
##### 产生数据集 #####
# y = w1*x1 + w2*x2
np.random.seed(1)
#高斯模型
x_1 = np.random.normal(6,1,size=100)
x_2 = np.random.normal(3,1,size=100)
y=np.ones(100)
c0 = np.array([x_1,x_2,y]).T
x_1 = np.random.normal(3,1,size=100)
x_2 = np.random.normal(6,1,size=100)
y=np.zeros(100)
c1 = np.array([x_1,x_2,y]).T
#将数据整合
all_data=np.vstack((c0,c1))
#数据打乱
np.random.shuffle(all_data)
#训练集和测试集
train_data_x=all_data[:150,:2]
train_data_y=all_data[:150,-1]
test_data_x=all_data[150:,:2]
test_data_y=all_data[150:,-1]
w = np.random.rand(2,1)
def loss_data(y,pred_y):
return -np.mean( y*np.log(pred_y) + (1-y)*np.log(1-pred_y))
def sigmod(z):
return 1/(1+np.exp(-z))
learn_rate=0.001 #学习率
loss_list=[]
for i in range(1000):
pred_y=sigmod( np.dot(w.T,train_data_x.T))
loss=loss_data(train_data_y,pred_y)
#计算梯度
grad = -np.mean(train_data_x*(train_data_y-pred_y).T,axis=0)
w = w - (learn_rate*grad).reshape(2,1)
loss_list.append(loss)
if i%10 ==1:
print("i: %d,loss: %f"%(i,loss))
if loss<0.1:
break
#绘制结果图
plt.scatter(c0[:, 0], c0[:, 1])
plt.scatter(c1[:, 0], c1[:, 1])
x=np.arange(10)
#w1*x+w2*y=0
y=-(w[0]*x)/w[1]
plt.plot(x,y)
plt.show()
#测试
pred_y=np.dot(w.T,test_data_x.T)
yy=np.array(pred_y>0,dtype=int).flatten()
rate=np.sum(test_data_y==yy)/len(yy)
print(rate)
结果: