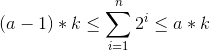买表(【CCF】NOI Online能力测试3 入门组)
题目描述
Jimmy 到 Symbol 的手表店买手表,Jimmy 只带了 nn 种钱币,第 ii 种钱币的面额为 ki 元,张数为 ai 张。Symbol 的店里一共有 m 块手表,第 i 块手表的价格为 ti 元。
Symbol 的手表店不能找零,所以 Jimmy 只能在凑出恰好的钱数时才能购买一块手表。现在对于店里的每块手表,Jimmy 想知道他能不能凑出恰好的钱数进行购买。
输入格式
第一行两个空格分隔的整数 n 和 m 表示钱币数与手表数。
接下来 nn 行每行两个空格分隔的整数 ki 和 ai 表示钱币的面额和张数。
第 n+2 行,共 m 个用空格分隔的整数 ti,表示每块手表的价格。
输出格式
一共 m 行,对于第 i 行,如果能凑出恰好的钱数购买第 i 块手表则输出 Yes 否则输出 No,注意只有首字母大写。
输入样例
3 5
1 2
5 1
6 3
3 19 21 1 7输出样例
No
Yes
No
Yes
Yes样例解释
- 第二块手表 19=6×3+1=6×2+5+1×2,可以恰好凑出。
- 第四块手表 1=1×1,可以恰好凑出。
- 第五块手表 7=5+2×1=6×1+1,可以恰好凑出
解法1:
思路分析:此题转化为子集和问题即可解决
C++代码如下:
#include
using namespace std;
int x=0,q[100000010],n,m,nn=0;//n为钱币有多少种种类 ,nn为钱币总张数
void FixedSum(int* a, int num, int t, int sum)
{
if(sum == 0)
x=1;
else
{
if(t == num)
return ;
else
{
if(sum - a[t] >= 0)
FixedSum(a, nn, t + 1, sum - q[t]) ;
if(sum >= 0)
FixedSum(a, nn, t + 1, sum) ;
}
}
}
int main()
{
cin>>n>>m;
int k,a;
for(int i=0;i>k>>a;
for(int j=0;j>sum;
FixedSum(q, nn, 0, sum);
if(x)
cout<<"Yes"< 解法2:
思路分析:
1.此题目可以转换为多重背包问题,然后基于二进制优化
2.什么是二进制优化?
1~n以内的数,都能够通过n进制以内的数组合得到,那我们这里用二进制(n=2)
简单来说,就是把一个数字分成 (1 2 4 8.........最大数) 这样下去的类型
以19为例,如果我们拆分成1,2,4,8,3
其实就是相加小于等于该数的2的幂次方(1,2,4,8)和19与和的差值3
对应到本题目,即a张面额为k的钱币,需要组合出1*k,……a*k。
构造1*k+2*k+……+2∧n+x=a*k
3.数据量太大,用bool数组可能得不到满分,我们可以用bitset
C++的 bitset 在 bitset 头文件中,它是一种类似数组的结构,它的每一个元素只能是0或1,每个元素仅用1bit空间
bitset默认构造为0,bitset[i]=1代表可以购买价值i元的手表
我们在组合时,如对于2^j来说
for(i=500000;i>=0;i--)
if(watch[i]==1)
watch[i+2^j*k]=1;这相当于
temp=watch<
AC的C++代码如下:
#include
using namespace std;
bitset<500005> watch;//默认为1,若值为1代表钱数能凑出
bitset<500005> temp;
int main()
{
int n,m,i,j,a,k,t;
cin>>n>>m;
watch[0]=1;
for(i=0;i>k>>a;
for(j=1;a>=j;j*=2)
{
temp=watch<>t;
if(watch[t])
cout<<"Yes"<