数据结构和算法笔记

据学过数据结构和算法的同级与师兄师姐们的诉苦，本人对数据结构产生了浓厚的兴趣，而且在编程比赛中吃过没学过算法的亏，故而一有空就跑去跟着学数据结构，想借此提升能力，开启一段新的旅程。

大O记法

“大O记法”：在这种描述中使用的基本参数是 n，即问题实例的规模，把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order)，比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时，运行时间至多将以正比于 f(n)的速度增长。
实例如下：

Temp=i;
i=j;
j=temp;                    

上图取的答案是O(1)。

sum=0；                 （一次）
  for(i=1;i<=n;i++)     （n次 ）
  for(j=1;j<=n;j++) （n^2次 ）
     sum++；       （n^2次 ）
解：T(n)=2n^2+n+1 =O(n^2)

上图取的答案是O(n^2)。

for (i=1;i<n;i++)
    {
        y=y+1;         ①   
        for (j=0;j<=(2*n);j++)    
           x++;        ②      
    }         
解： 语句1的频度是n-1
          语句2的频度是(n-1)*(2n+1)=2n^2-n-1
          f(n)=2n^2-n-1+(n-1)=2n^2-2
          该程序的时间复杂度T(n)=O(n^2).     

通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求。当直接要求让我们求“复杂度”时，通常指时间复杂度。

线性表

线性表可以记为（a1,…,ai-1,ai,ai+1,…an），则是表中ai-1领先于ai，ai领先于ai+1，称ai-1是ai的直接前驱元素，ai+1是ai的直接后继元素。

抽象：

	是指抽取出事物具有的普遍性的本质。它要求
抽出问题的特征而忽略非本质的细节，是对具体事物
的一个概括。抽象是一种思考问题的方式，它隐藏了
繁杂的细节。

抽象数据类型的标准格式：
ADT

抽象数据类型名

Data

数据元素之间的逻辑关系的定义

Operation

操作

endADT

线性表的一些基本操作组合：

ListLength(L);

线性表长度

GetElem(L,i,*e);

获取线性表元素

LocateElem(L,e);

检查是否存在此元素

ListInsert(*L,i,e);

字第i个位置插入元素

线性表的顺序存储结构

线性表有两种物理存储结构：顺序存储结构和练市存储结构。
线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

简单例子：

//进行结构封装
#define MAXSIZE 20//定义一个最大的长度
typedef int ElemType;//设置为整形
typedef struct
{
	ElemType data[MAXSIZE];//ElemType是随机类型的意思（字节为单位）
	int length;
}SqList;//线性表

线性表类似于数组，但有所不同，其当前长度初始化后仍然能发生改变。线性表从1开始。
LOC表示获得存储位置的函数。

计算公式：LOC（ai+1）=LOC（ai）+(i-1)*c

我们可以随时计算出线性表中任意位置的地址，不管它是第一个还是最后一个，都是相同的时间。那么它的存储时间性能当然就为O（1），这类的我们通常称为随机存储结构。

例子2：（插入元素）

线性表的顺序存储结构，在存、读数据时，不管是哪个位置，时间复杂度都是O（1）。而在插入或删除时，时间复杂度都是O(n)。

优点：

1. 无须为表示表中元素之间的逻辑关系而增加额外的存储空间。
2. 可以快速地存取表中任意位置的元素。

缺点：

 1. 插入和删除操作需要移动大量元素。
 2. 当线性表长度变化较大时，难以确定存储空间的容量。
 3. 容易造成存储空间的“碎片”。

我们把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成数据元素称为存储映像，称为结点。

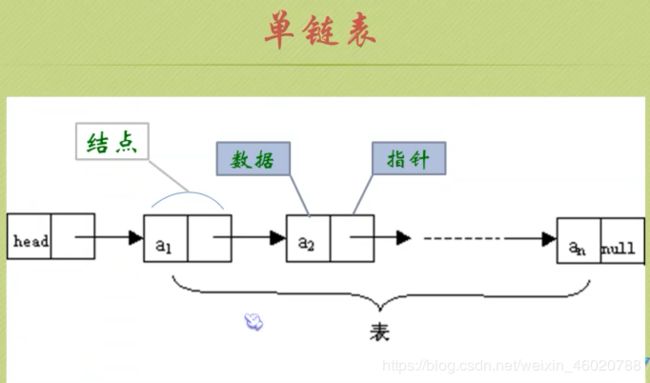
头指针与头结点

头指针：
1.头指针是指链表指向第一个结点的指针，若链表有 头结点，则是指向头结点的指针。
2. 头指针具有标识作用，所以常用头指针冠以链表的名字。（指针变量的名字）。
3. 无论链表是否为空，头指针均不为空。
4. 头指针是链表的必要元素。
头结点：

 1. 头结点时为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义（但也可以用来存放链表的长度）。
 2. 有了头结点，对在第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了。
 3. 头结点不一定时链表的必须要素。

实例：（查找元素）“工作指针后移”

利用单链表插入结点：

删除结点：

单链表结构的比较
单链表第一部分是遍历查第i个元素，第二部分就是实现插入和删除元素。时间复杂度为O（n）。
线性表可以在知道具体结点位置的情况下可以直接一次性赋值转换，时间复杂度仅仅为O（1）。

头插法与尾插法

头插法从一个空表开始，生成新结点，读取数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，知道结束为止。
简单来说：就是把新加进的元素放在表头后的第一个位置：

 1. 先让新节点的next指向头节点之后。
 2. 然后让表头的next指向新节点。

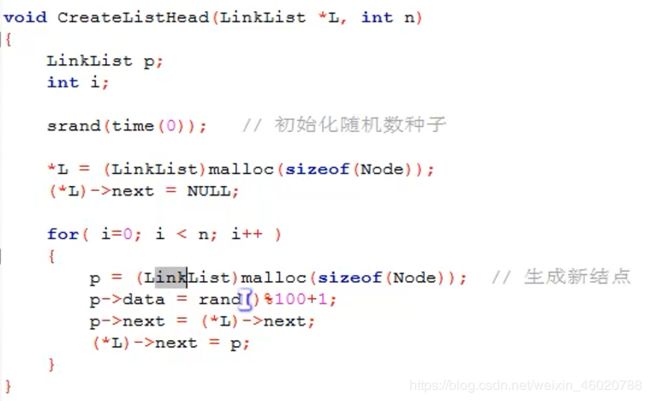
尾插法：
头插法虽然建立链表的算法简单，但生成的链表中结点的次序和输入的顺序相反。我们可以将新结点都插入到最后，这种算法称之为尾插法。

单链表与顺序存储结构的对比

存储分配方式：

顺序存储结构用一段连续的存储单元依次存储线性表的数据元素。
单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素。

时间性能：
查找

	顺序存储结构O(1)。
	单链表O(n)。

插入和删除

	顺序存储结构需要平均移动表长一般的元素，时间为O(n)。
	单链表在计算出某位置的指针后没插入和删除时间仅为O(1)。

空间性能：

顺序存储结构需要预分配存储空间，分大了容易造成空间浪费，分小了容易发生溢出。
单链表不需要分配存储空间，只要有就可以分配，元素个数也不受限制。

总结：

 若线性表需要平方查找，很少进行插入和删除操作时，宜采用顺序存储结构。
 若需要平方插入和删除时，宜采用单链表结构。

静态链表

用数组描述的链表叫做静态链表，这种描述方法叫做游标实现法。