Python123 练习7
文章目录
- 1. 梯形法计算积分值
- 2. 哥德巴赫猜想
- 3. 鸡兔同笼B
- 4. 与7无关的数
- 5. 完美立方数
- 6. 高次方程求根
- ==如果文章内容或代码有问题,或者其他问题,可以评论或者私信==
1. 梯形法计算积分值
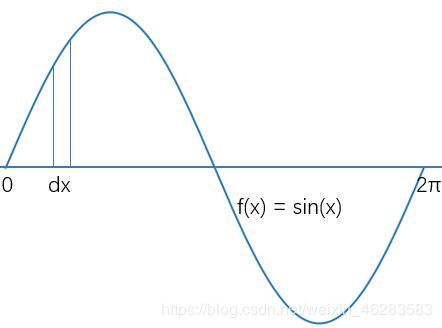
计算函数曲线与x轴包围的面积,计算函数曲线在区间(a,b)与x轴包围的面积,可将这个区域平行于y轴切分成相等宽度的小梯形,每个梯形的面积可近似求出,所有梯形面积的和就是函数曲线与x轴包围的面积,也就是函数在给定区间的积分值,dx越小,梯形近似度越高,计算结果越精确,也就是说区间切分段的越多,结果越精确。
参考下图,计算函数sin(x)在区间(a,b)与x轴包围的面积,a,b由用户输入,区间切分多少段也由用户输入。
- 输入格式: 第一行是由空格分隔的两个实数,代表积分区间。第二行是一个正整数,代表切分数量
- 输出格式: 积分值,结果保留2位小数
方法
import math
a, b = map(float, input().split())
c = int(input())
d = (b - a) / c # 梯形的高度
s = 0
for i in range(c):
x = math.fabs(math.sin(a)) # 梯形上底,绝对值保证为正数
a += d
y = math.fabs(math.sin(a)) # 梯形下底,绝对值保证为正数
z = (x + y)*d/2 # 单个梯形面积
s += z # 所有梯形面积总和
print('{:.2f}'.format(s))
2. 哥德巴赫猜想
数学领域著名的“哥德巴赫猜想”的大致意思是:任何一个大于2的偶数总能表示为两个素数之和。比如:24=5+19,其中5和19都是素数。本实验的任务是设计一个程序,验证20亿以内的偶数都可以分解成两个素数之和。
- 输入格式:输入在一行中给出一个(2, 2 000 000 000]范围内的偶数N。
- 输出格式:在一行中按照格式“N = p + q”输出N的素数分解,其中p ≤ q均为素数。又因为这样的分解不唯一(例如24还可以分解为7+17),要求必须输出所有解中p最小的解。
方法1 函数模块化
def isprime(num): # 判断是否为素数
if num == 1:
return False
elif num == 2:
return True
else:
for i in range(1, num):
if num % i == 0:
y = i
if y == 1:
return True
def list_prime(num): # 将比输入数小的所有素数合并成列表
a = []
for i in range(1, num + 1):
if isprime(i):
a.append(i)
return a
def check(num): # 检查所有可能的两个素数组合
global b1
b1 = []
global b2
b2 = []
c = list_prime(num)
for i in c:
for j in c:
if i + j == num:
b1.append(i)
b2.append(j)
return b1 and b2
def begin(): # 按要求输出
num = eval(input())
list_prime(num)
check(num)
p = b1[0]
q = b2[0]
print('N = {} + {}'.format(p, q))
begin()
方法2一般形式
num = eval(input())
a = []
for i in range(2, num): # 将输入数范围内的所有素数加入列表
if i == 2:
a.append(i)
else:
for j in range(1, i): # 判断是否为素数
if i % j == 0:
y = j
if y == 1:
a.append(i)
b1 = []
b2 = []
for k in a: # 检查所有可能的两个素数组合
for z in a:
if k + z == num:
b1.append(k)
b2.append(z)
p = b1[0] # 按要求输出
q = b2[0]
print('N = {} + {}'.format(p, q))
3. 鸡兔同笼B
一个笼子里面关了若干只鸡和兔子(鸡有2只脚,兔子有4只脚,没有例外),已经知道了笼子里面脚的总数feets,则笼子里至少有多少只动物,至多有多少只动物?
输入格式: 第一行输入一个正整数,表示测试数据的组数n。接下来的n行,每行一个整数,代表脚的数量。
输出格式:输出包含n行,每行对应一个输入,包含两个正整数,第一个是最少的动物数,第二个是最多的动物数,两个正整数间用一个空格分开,如果没有满足要求的答案,则输出用空格分隔的两个0。
方法
def result(x): # 函数模块化,参数为脚的数量
if x >= 4: # 当脚小于4时不可能有兔子
a = x // 4 # 兔子数量最大值
b = x // 2 # 鸡的数量最大值
c = []
for i in range(0, a + 1):
for j in range(0, b + 1):
if 4 * i + 2 * j == x:
z = i + j
c.append(z)
if i == a and b == j and c == []:
print('0 0')
if c:
c.sort()
result_min = c[0]
result_max = c[-1]
print('{} {}'.format(result_min, result_max))
else:
if x == 2:
print('1 1')
else:
print('0 0')
def input_n(num): # 通过组数,确定需要输入的几行,并计算动物数量
t = 0
while t < num:
x = int(input())
result(x)
t = t + 1
num = eval(input()) # 获取组数
input_n(num)
4. 与7无关的数
一个正整数,如果它能被7整除,或者它的十进制表示法中某一位的数字为7,则称其为与7相关的数
求所有小于n(n < 100)的与7无关的正整数以及他们的平方和。
输入格式:输入为一个正整数。
输出格式:第一行为所有与7无关的数,以列表形式输出,逗号分开。第二行为他们的平方和。
方法
num = eval(input())
x = []
y = []
for i in range(1,num): # 小于输入n的所有整数列表
x.append(i)
for j in range(1,num): # 遍历每一个整数
if j % 7 == 0: # 若能整除7,加入与7相关的数的列表
y.append(j)
else: # 若不能整除7,再判断是否有一位是7
if j % 10 == 7: # 个位
y.append(j)
elif j // 10 == 7: # 十位,数小于100,仅需检测到十位
y.append(j)
for k in y: # 将所有整数列表中的所有与7相关的数移除
x.remove(k)
x.sort() # 列表升序排序
result = 0
for l in x: # 遍历所有与7无关的数,并递归相加所有值
result += l*l
print(x) #打印结果
print(result)
5. 完美立方数
费马大定理断言,当整数n > 2时,关于a,b,c的方程a ** n = b ** n + c ** n 没有正整数解。该定理被提出来后,历经三百多年,经历多人猜想辩证,最终在1995年被英国数学家安德鲁.怀尔斯证明。
当然,可以找到大于1的4个整数满足完美立方等式: a * *3 = b ** 3 + c ** 3 + d ** 3 (例如12 ** 3 = 6 ** 3 + 8 ** 3 + 10 ** 3)
编写一个程序,对于任意给定的正整数N(N<=100),寻找所有的四元组(a,b,c,d),满足a ** 3 = b ** 3 + c ** 3 + d ** 3.其中 1 < a,b,c,d <=N.
- 输入格式:正整数N(N <= 100)
- 输出格式:按照a的值从小到大,每行输出一个完美立方等式,其中b,c,d按照非降序排列输出。若两个完美立方式中a值相同,则b值小的先输出;在b值相等的情况下,c值小的先输出,在b,c都相等的情况下,d值小的先输出。
方法
x = int(input())
for a in range(2,x+1): # 根据题目条件,限定每一个数的范围,去除重复
for b in range(2,a):
for c in range(b,a):
for d in range(c,a):
if pow(a,3) == pow(b,3)+pow(c,3)+pow(d,3): # 满足完美立方数条件的数
print("Cube = {},Triple = ({},{},{})".format(a,b,c,d))
6. 高次方程求根
有函数
f ( x ) = x 5 − 15 x 4 + 85 x 3 − 225 x 2 + 274 x − 121 f(x)=x^5-15x^4+85x^3-225x^2+274x-121 f(x)=x5−15x4+85x3−225x2+274x−121
已知f(1.5)>0,f(2.4)<0,且在[1.5,2.4]区间只且只有一个根,求该根。要求四舍五入到小数点后6位
输出格式:该方程在[1.5,2.4]区间的根,精确到小数点后6位
方法
def f(x): # 封装 高次方程带入求值 的函数
result = pow(x, 5) - 15 * pow(x, 4) + 85 * pow(x, 3) - 225 * pow(x, 2) + 274 * x - 121
return result
a = 1.5
b = 2.4
c = (a + b) / 2 # 浮点型不可能完全等于零
while abs(f(c)) > 1e-6: # 所以为了判断需要,根据题目一个范围1e-6,即10的-6次方
if f(a) * f(c) < 0: # 若abs(f(c))精度超过6时的值,都当作等于0;
b = c # 通过二分法计算、缩减范围
else:
a = c
c = (a + b) / 2
print("{:.6f}".format(c))