富**面试

【一】前言

当天下午2点面试了珠海格**,下午坐地铁回到了学校，在电子科技大学有一场宣讲会，会现场进行笔试，当时感觉还行，公司应该是一个好公司，就毅然地决定去试一试，当时山歌会议厅，惊呆了，全场坐满了人，还很多的人坐在最后面，宣讲结束以后，因为笔试的人很多，导致会场无法做那么多的，又移步到其他的教师进行笔试。笔试的体还行，有的做过，有的不知道，总体的感觉还行。结果笔试过了收到了面试的邀请。

【二】一面

• 2.1 计算机网络的tcp和udp的差别，分别使用的场景？

方面	TCP	UDP
连接	面向连接	无连接
可靠	TCP利用握手，确认，重传机制，拥塞控制，顺序控制，提供了可靠性保证	UDP可能会丢失，不保证数据可靠
有序性	TCP利用序列号，保证了消息的顺序交付，虽然到达可能无序，但是TCP最终会排序	UDP不具备有序性
速度	慢	快
连接	每一条TCP连接只能是点到点的	UDP支持一对一，一对多，多对一和多对多的交互通信
资源消耗	TCP对系统资源要求较多	UDP对系统资源要求较少
实效性	TCP传输数据的控制程序较多，大幅度降低了数据传输的实时性	UDP协议简单，数据实时性较高

使用场景：
TCP:
对数据传输的质量有较高要求，但对实时性要求不高。比如HTTP，HTTPS，FTP等传输文件的协议以及POP，SMTP等邮件传输的协议，应选用TCP协议。
UDP:
只对数据传输的实时性要求较高，但不对传输质量有要求。比如视频传输、实时通信等，应选用UDP协议


2.2 TCP的深入了解：

名称	说明
重传机制	当TCP发出一个段后，它启动一个定时器，等待目的端确认收到这个报文段。如果不能及时收到一个确认，将重发这个报文段。 (超时重发)
有序机制	既然TCP报文段作为IP数据报来传输，而IP数据报的到达可能会失序，因此TCP报文段的到达也可能会失序。将收到的数据以正确的顺序交给应用层
拥塞控制	TCP还能提供流量控制。TCP连接的每一方都有固定大小的缓冲空间。TCP的接收端只允许另一端发送接收端缓冲区所能接纳的数据。这将防止较快主机致使较慢主机的缓冲区溢出。TCP使用的流量控制协议是可变大小的滑动窗口协议
确认机制	TCP协议中，接收方成功接收到数据后，会回复一个ACK数据包，表示已经确认接收到ACK确认号前面的所有数据

• 2.3 Tcp的三次握手，四次挥手的过程
  TCP的三次握手
  

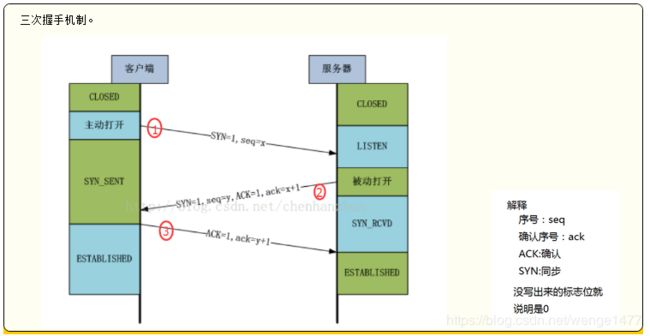
第一次握手
客户端向服务器发出连接请求报文，这时报文首部中的同部位SYN=1，同时随机生成初始序列号 seq=x，此时，TCP客户端进程进入了 SYN-SENT（同步已发送状态）状态。TCP规定，SYN报文段（SYN=1的报文段）不能携带数据，但需要消耗掉一个序号。这个三次握手中的开始。表示客户端想要和服务端建立连接

第二次握手
TCP服务器收到请求报文后，如果同意连接，则发出确认报文。确认报文中应该 ACK=1，SYN=1，确认号是ack=x+1，同时也要为自己随机初始化一个序列号 seq=y，此时，TCP服务器进程进入了SYN-RCVD（同步收到）状态。这个报文也不能携带数据，但是同样要消耗一个序号。这个报文带有SYN(建立连接)和ACK(确认)标志，询问客户端是否准备好。
第三次握手
TCP客户进程收到确认后，还要向服务器给出确认。确认报文的ACK=1，ack=y+1，此时，TCP连接建立，客户端进入ESTABLISHED（已建立连接）状态。TCP规定，ACK报文段可以携带数据，但是如果不携带数据则不消耗序号。这里客户端表示我已经准备好。

2.4 为什么要三次握手呢?
为了防止失效的连接请求报文段
1、client发送了第一个连接的请求报文，但是由于网络不好，这个请求某个网络节点中滞留了，直到某个时间才到达server。

2、本来这已经是一个失效的报文，但是server端接收到这个请求报文后，还是会想client发出确认的报文，表示同意连接。

3、但是client是不会理睬server的确认信息，也不会向服务端发送确认的请求，但是server认为新的连接已经建立起来了，并一直等待client发来数据，这样很多资源就没白白浪费掉了。

采用三次握手就是为了防止这种情况的发生，server会因为收不到确认的报文，就知道client并没有建立连接。这就是三次握手的作用


2.5 TCP的四次挥手

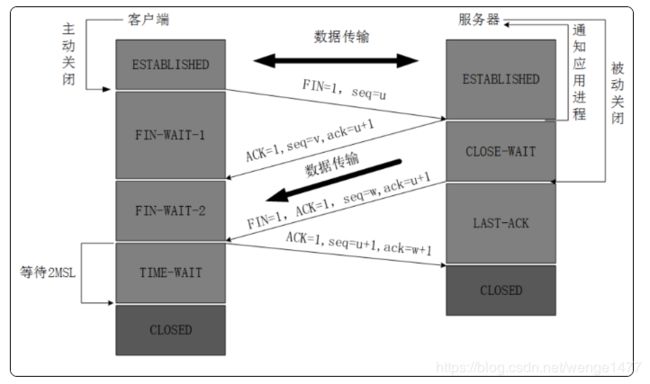
第一次挥手
TCP发送一个FIN(结束)，用来关闭客户到服务端的连接。客户端进程发出连接释放报文，并且停止发送数据。释放数据报文首部，FIN=1，其序列号为seq=u（等于前面已经传送过来的数据的最后一个字节的序号加1），
此时，客户端进入FIN-WAIT-1（终止等待1）状态。 TCP规定，FIN报文段即使不携带数据，也要消耗一个序号
第二次挥手
服务端收到这个FIN，他发回一个ACK(确认)，确认收到序号为收到序号+1，和SYN一样，一个FIN将占用一个序号。
服务器收到连接释放报文，发出确认报文，ACK=1，ack=u+1，并且带上自己的序列号seq=v，此时，服务端就进入了CLOSE-WAIT（关闭等待）状态。
TCP服务器通知高层的应用进程，客户端向服务器的方向就释放了，这时候处于半关闭状态，即客户端已经没有数据要发送了，但是服务器若发送数据，客户端依然要接受。这个状态还要持续一段时间，也就是整个CLOSE-WAIT状态持续的时间。
第三次挥手
服务端发送一个FIN(结束)到客户端，服务端关闭客户端的连接。
服务器将最后的数据发送完毕后，就向客户端发送连接释放报文，FIN=1，ack=u+1，由于在半关闭状态，服务器很可能又发送了一些数据，假定此时的序列号为seq=w，此时，服务器就进入了LAST-ACK（最后确认）状态，等待客户端的确认。
第四次挥手
客户端发送ACK(确认)报文确认，并将确认的序号+1，这样关闭完成。
客户端收到服务器的连接释放报文后，必须发出确认，ACK=1ack=w+1，而自己的序列号是seq=u+1，此时，客户端就进入了TIME-WAIT（时间等待）状态。
注意此时TCP连接还没有释放，必须经过2∗∗MSL（最长报文段寿命）的时间后，当客户端撤销相应的TCB后，才进入CLOSED状态。

服务器只要收到了客户端发出的确认，立即进入CLOSED状态。同样，撤销TCB后，就结束了这次的TCP连接。可以看到，服务器结束TCP连接的时间要比客户端早一些。


2.6 为什么要采用四次挥手

为了确保数据能够完成传输
关闭连接时，当收到对方的FIN报文通知时，它仅仅表示对方没有数据发送给你了；但未必你所有的数据都全部发送给对方了，所以你可以未必会马上会关闭SOCKET,也即你可能还需要发送一些数据给对方之后，再发送FIN报文给对方来表示你同意现在可以关闭连接了，所以它这里的ACK报文和FIN报文多数情况下都是分开发送的。

可能有人会有疑问，tcp我握手的时候为何ACK(确认)和SYN(建立连接)是一起发送。挥手的时候为什么是分开的时候发送呢.

因为当Server端收到Client端的SYN连接请求报文后，可以直接发送SYN+ACK报文。其中ACK报文是用来应答的，SYN报文是用来同步的。但是关闭连接时，当Server端收到FIN报文时，很可能并不会立即关闭 SOCKET，所以只能先回复一个ACK报文，告诉Client端，“你发的FIN报文我收到了”。只有等到我Server端所有的报文都发送完了，我才能发送FIN报文，因此不能一起发送。故需要四步挥手。

• 2.7 Tcp的报文头包含有哪些信息
  

• 2.8 数字证书？
  
  
  

• 2.9 对称加密和非对称加密
  

• 2.10 同步异步？

• 2.11 线程的理解，或者说是使用过程？

• 2.12 为什么使用线程池？

• 2.13 数据库的几个特性？每个特性解释

• 2.14 数据库事务的问题？

上面的2.10-2.14之间的请移步到博客：https://blog.csdn.net/wenge1477/article/details/90481125

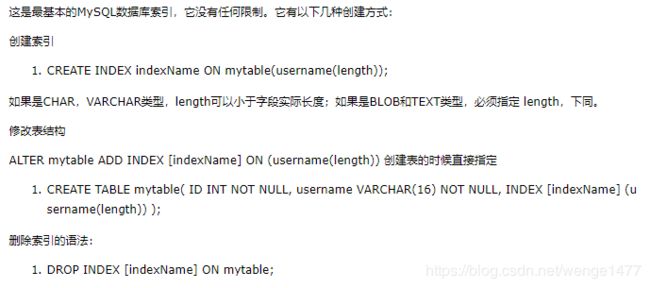
• 2.15 数据库索引有哪些？以及存储的结构

1、普通索引

2、唯一性索引

3、主键索引

4、组合索引

前方高能>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
手撕代码：

• 有n步，一次可走1步，或者2步，有多少种走法？（代码实现）

//第一种解法,使用两层递归的方式求解
public static int waiTiao(int current, int all) {
        if (current > all) {
            return 0;
        }
        if (current == all) {
            return 1;
        }
        return waiTiao(current + 1, all) + waiTiao(current + 2, all);
}


//第二种解法，使用动态规划来解决这个问题
public static int waitaio(int tag) {
        if (tag <= 2) {
            return tag;
        }
        int count1 = 1;
        int count2 = 2;
        for (int i = 3; i <= tag; i++) {
            int current = count1 + count2;
            count1 = count2;
            count2 = current;
        }
        return count2;
}

• 有n层楼高，有两个玻璃球，用最少的测量次数，要测量出球能在的最高层放下而不摔坏？（思路）

//第一种思路，采用二分法
1、先从50层丢，如果50层没有碎，那么就到75层丢。
2、如果碎了就只剩下一个球，就只能从50层一层一层地往上面加，直到临界层

//第二中思路，采用分区间丢
1、先从10层丢，20层丢，30层丢
2、如果以层碎了，那么就需要从上一次丢的层，一步一步的加，直到临界层

• 有两个拍好序的数组AB，AB两个中可能有重复的元素，如何使用最小的- 时间复杂度判断B是否为A的子集（代码实现）

//思路一、采用二分法来求解这个问题


//思路二、采用hashMap来解决这个问题
public static boolean getMapAns(int[] array1,int[] array2){
        Map<Integer,Integer> map = new HashMap<>();
        for (int i = 0; i < array1.length; i++) {
            map.put(array1[i],map.getOrDefault(array1[i],0)+1);
        }
        for (int i = 0; i <array2.length ; i++) {
            map.put(array2[i],map.getOrDefault(array2[i],0)-1);
        }
        for (int i = 0; i <array2.length ; i++) {
            if(map.get(array2[i])!=0){
                return false;
            }
        }
        return true;
}

【三】二面

• 3.1 计算机网络 tpc/udp？

• 3.2 tcp的报文头/滑动窗口/拥塞控制？

  3.1-3.2 这两个问题和上面已经有回答了

• 3.3 get和post的差别？
  这个请移步到博客：https://blog.csdn.net/wenge1477/article/details/99443121
  
  

• 3.4 对递归的理解？递归需要的那些东西或者特征才需要进行递归？

递归就是把大问题转换为小问题，需要有递归的出口。

比如我们知道的数据结构树：
根节点，左子树，右子树
我们的左右子树也是一颗树
那么就有了天然的递归特性
对当前根节点的操作，那么递归也是适应于我们的左右子树，因为他们也是一棵树
这样把大树，最后到我们的叶子节点求解出来

• 3.5 浏览器的缓存的过程？如何进行缓存的？

• 3.6 加密/对称加密和非对称加密的差别？
  这个再上面的问题中已经进行解决了

• 3.7 操作系统中的用户态？
  
  

• 3.8 Java的Jvm？整个流程？
  这个问题请移步到博客：https://github.com/CyC2018/CS-Notes/blob/master/notes/Java%20%E8%99%9A%E6%8B%9F%E6%9C%BA.md#%E4%B8%80%E8%BF%90%E8%A1%8C%E6%97%B6%E6%95%B0%E6%8D%AE%E5%8C%BA%E5%9F%9F

**前方高能>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>**

• 猴子分桃的线性规划的问题？（答案)

数学题，用线性方程组求解

• 循环队列（代码）

public class myQueue {
    int front;
    int rear;
    int queueList[];
    int MaxLen=0;
    public myQueue(int MaxLen) {
        // TODO Auto-generated constructor stub
        queueList=new int[MaxLen];
        front=0;
        rear=0;
        this.MaxLen=MaxLen;
    }
    public boolean isEmpty() {
        if(front==rear){
            return true;
        }
        return false;
    }
    public boolean isFull(){
        if(((rear+1)%MaxLen)==front){
            return true;
        }
        else{
            return false;
        }
    }
    public void queueFront(int getFront){
        if(isEmpty()==false){
            getFront=queueList[(front+1)%MaxLen];
        }
        else {
            System.out.println("ERROR:Queue is Empty");
            return;
        }
    }
    public void enQueue(int enData) {
        if(isFull()==false){
            rear=(rear+1)%MaxLen;
            this.queueList[rear]=enData;
        }
        else{
            System.out.println("ERROR:Queue is Full");
            return;
        }

    }

    public void outQueue() {
        if(isEmpty()==false){
            front=(front+1)%MaxLen;
        }
        else {
            System.out.println("ERROR:Queue is Empty");
            return;
        }

    }
}

• 有一个数组里面包含R,G,B,这三种元素，元素的个数不确定，元素的位置不确定，如何以最少的时间复杂度把这个数组排好序？（代码实现，变种的快速排序)

//思路是因为是只有三个元素，那么可以采用变种的快速排序
public static void getAns(char[] array){
        int k=0;
        int l=array.length-1;
        for (int i = 0; i < array.length; i++) {
            char t = array[i];
            if(t=='R'){
                swarp(array,i,k);
                k++;
            }
            if(t=='B'){
                swarp(array,i,l);
                l--;
            }
        }
    }
    public static void swarp(char[] array,int i,int j){
        char t = array[i];
        array[i]=array[j];
        array[j]=t;
    }

【四】三面

问一些其他的问题，在校表现，以及一些个人经历等等？