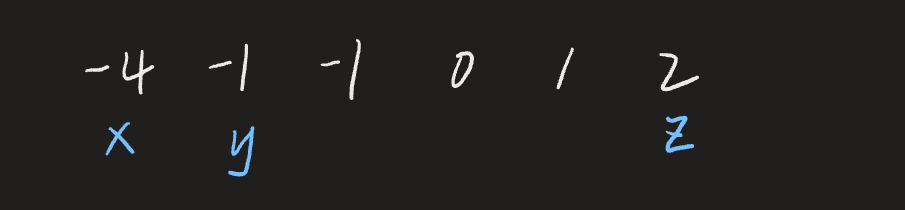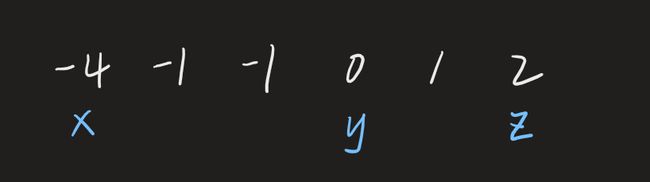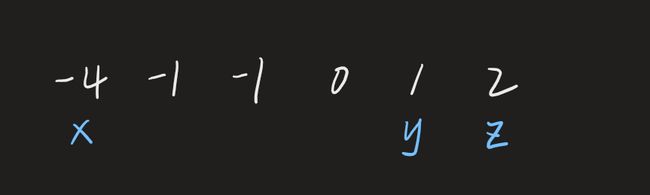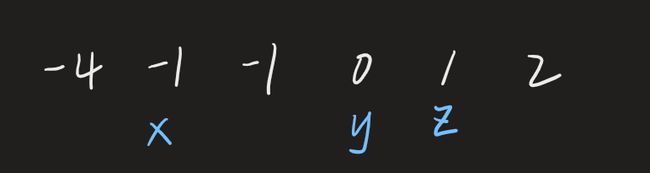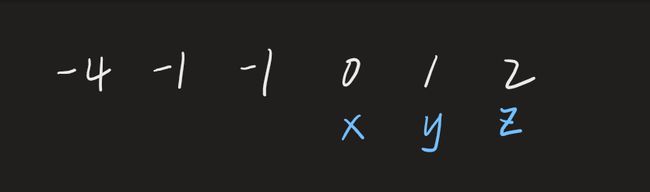LeetCode 15. 3Sum, 三数之和 ,C#
前言
本文介绍了 LeetCode 第 15 题 , “3Sum”, 也就是 “三数之和” 的问题.
本文使用 C# 语言完成题目,介绍了2种方法供大家参考。
题目
English
LeetCode 15. 3Sum
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
中文
LeetCode 15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:
答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
解决方案
看到题目,三层循环的暴力法就出现在脑海,但是提交后会报超时,并且这也不是我们要的结果,我们需要的是通过题目来找寻方法,而不是仅仅将题目给解决。下文将介绍两种方法供读者参考。
第一种方法 是 双指针法。
第二种方法 是 哈希表法。
方法一:双指针法
若一组解为 (x,y,z) , 则该方法是先确定x,然后使用双指针同时寻找y和z。首先我们对nums进行排序,然后取第一个值为x,并使用双指针指向剩余部分的头和尾,验证三数之和是否为0,若是,则将三数作为一组解 并保存下来,若否,则判断和大于0还是小于0,并根据情况移动指针。
由于nums数组会被排序,所以我们可以根据局部情况来移动指针,并不断的寻找下一组解。
比如对于题目示例 nums=[ -1, 0 , 1, 2, -1, -4] :
第一步先进行排序,得到 nums=[ -4, -1, -1, 0, 1, 2].
第二步开始双指针法找寻解。令x=-4, y和z分别指向剩余部分的头和尾:
因为 此时 x+y+z=-4+(-1)+2=-3 < 0 ,所以y+z太小了,需要变大,所以y需要向右移动。
移动过程中要注意跳过重复值,避免结果三元组重复。 y移动到0的位置,此时三数之和为-2,还是小于0,为了增大,y还是需要向右移动。
此时三数之和为-1,但y已经无法继续向右移动了。说明当x取-4时,无法得到三元组满足和为0.
接下来将x右移一位,并重置y和z为剩余部分的头和尾。
此时三数之和为0,得到一组解为(-1,-1,2). 当x取-1时,还可能右其他解,为了保持三数和为0,y需要右移,z需要左移。
此时三数之和为0,得到一组解为(-1,0,1)。y和z已经不能再移动了,所以x右移,并且需要跳过重复值-1, 并充值y和z为剩余部分的头和尾。
此时三数之和为3 ≠ 0,且三个指针均无法再移动。所以整个过程结束,共有2组解。
参考代码:
public IList> ThreeSum(int[] nums)
{
IList> result = new List>();
int len = nums.Length;
if (len < 3) return result;
Array.Sort(nums);
for (int i = 0; i < len - 2; i++)
{
if (nums[i] > 0) break;
if (i > 0 && nums[i] == nums[i - 1]) continue; // 去重
int left = i + 1;
int right = len - 1;
while (left < right)
{
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0)
{
result.Add(new List() { nums[i], nums[left], nums[right] });
while (left < right && nums[left] == nums[left + 1]) left++; // 去重
while (left < right && nums[right] == nums[right - 1]) right--; // 去重
left++;
right--;
}
else if (sum < 0) left++;
else if (sum > 0) right--;
}
}
return result;
}
执行结果
执行结果 通过。 执行用时: 356ms, 内存消耗 35.5M
复杂度分析
时间复杂度:O(n^2)
i循环占用n,内层双指针占用n,所以是 O(n^2) .
空间复杂度:O(1)
常数数量的变量来存值。
方法二:哈希表法
方法一是确定x后同时寻找y和z,而方法二则是确定x和y后寻找z。我们在寻找z的过程中使用哈希表的O(1)寻找,所以最终时间复杂度仍然是O(n^2).
参考代码:
public IList> ThreeSum(int[] nums)
{
int len = nums.Length;
var result = new List>();
if (len < 3) return result;
Array.Sort(nums);
//map<值,lastIndex>
var map = new Dictionary();
for (int i = 0; i < len; i++)
{
if (map.ContainsKey(nums[i])) map[nums[i]] = i;
else map.Add(nums[i], i);
}
for (int i = 0; i < len - 2; i++)
{
if (nums[i] > 0) break;
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1; j < len - 1; j++)
{
if (j != i + 1 && nums[j] == nums[j - 1]) continue;
int numsK = 0 - nums[i] - nums[j];
if (map.ContainsKey(numsK) && map[numsK] > j)
result.Add(new List() { nums[i], nums[j], numsK });
}
}
return result;
}
执行结果
执行结果 通过。 执行用时: 448ms, 内存消耗 35.7M
复杂度分析
时间复杂度:O(n^2)
x占用n,y占用n,z是哈希表查询占用O(1),所以综合起来是O(n^2).
空间复杂度:O(1)
常数数量的变量来存储值。
参考资料汇总
题目:
https://leetcode-cn.com/problems/3sum/