基于Q-learning的机器人路径规划系统(matlab)
0 引言
Q-Learning算法是由Watkins于1989年在其博士论文中提出,是强化学习发展的里程碑,也是目前应用最为广泛的强化学习算法。Q- Learning目前主要应用于动态系统、机器人控制、工厂中学习最优操作工序以及学习棋类对弈等领域。
1 项目概述
Q学习在机器人路径规划领域有较为广泛的应用,由于其只需要与环境进行交互,且仅需感知当前状态和环境即可对下一步动作进行决策。
本研究以 MATLAB为基础,设计基于Q学习的最短路径规划算法,并考虑智能体的斜 向运动,更加符合实际情况。同时使用DQN网络对Q值更新进行一定的优 化,使得Q值表能够更加符合实际应用。
本次研究的具体步骤如下:
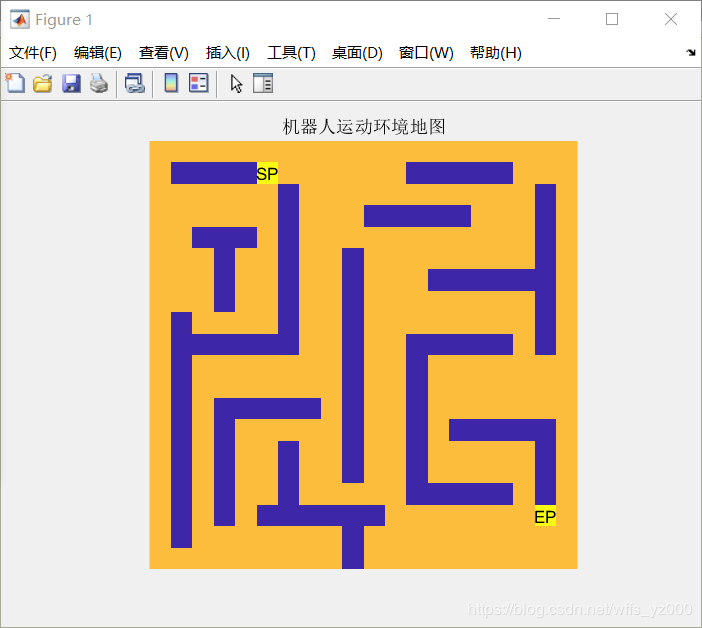
- 设计一个有障碍物的地图,用户可以修改障碍物布局,可以指定起点和终点;
- 使用MATLAB编程实现Q-learning算法,用于机器人规划最短路径,学习算法参数可以由用户设置;
- 使用用可视化界面演示Q值变化过程及最短路径探测过程。
2 Q-learning算法思想
Q-Learning算法是一种off-policy的强化学习算法,一种典型的与模型无关的算法。算法通过每一步进行的价值来进行下一步的动作。基于QLearning算法智能体可以在不知道整体环境的情况下,仅通过当前状态对下一步做出判断。
Q-Learning是强化学习算法中value-based的算法,Q是指在某一时刻的某一状态下采取某一动作期望获得的收益。环境会根据智能体的动作反馈相 应的回报,所以算法的主要思想就是将状态与动作构建成一张Q值表,然后根据Q值来选取能够获得最大的收益的动作。
3 算法步骤
- 初始化Q值表。构造一个n行n列(n为状态数)的 Q值表,并将表中的所有值初始化为零。
- 基于当前Q值表选取下一个动作a。初始状态时,Q值 均为零,智能体可有很大的选择空间,并随机选择下一步动作。随着迭代次数增加,Q值表不断更新,智能体 将会选择回报最大的动作。
- 计算动作回报。采用动作a后,根据当前状态和奖励,使用Bellman 方程更新上一个状态的Q(s, t)。
NewQ(s,a) = (1 − α)Q(s,a) + α(R(s,a) + γmaxQ′(s′,a′))
其中, NewQ(s,a)——上一个状态s和动作a的新Q值
Q(s,a)——当前状态s和动作a的Q值
R(s,a)——当前状态s和动作a的奖励r
maxQ′(s′,a′)——新的状态下所有动作中最大的Q值 - 重复步骤3,直到迭代结束,得到最终的Q值表。
- 根据Q值表选择最佳路径。
(二)算法改进
- 避免局部最优
Q-learning本质上是贪心算法。如果每次都取预期奖励最高的行为去 做,那么在训练过程中可能无法探索其他可能的行为,甚至会进入“局部 最优”,无法完成游戏。所以,设置系数,使得智能体有一定的概率采取 最优行为,也有一定概率随即采取所有可采取的行动。将走过的路径纳入 记忆库,避免小范围内的循环。 - 增加斜向运动
将斜向运动的奖励值设置为√2/ 2 ,取近似值0.707,可以避免出现如机器 人先向左上方移动再向左下方移动而不选择直接向左移动两格的情况。设 置为此值是根据地图的两格之间的相对距离确定的。
4 MATLAB实现代码
%% 基于Q-learning算法的机器人路径规划系统
clear
%% 首先创造一个机器人运动的环境
% n是该运动的运动环境的矩阵environment(n,n)的行列大小
n = 20;
% 新建一个全为1的n*n维environment矩阵
environment = ones(n,n);
%下面设置环境中的障碍物,将其在矩阵中标为值-100(可自行设置障碍物)
environment(2,2:5)=-100;
environment(5,3:5)=-100;
environment(4,11:15)=-100;
environment(2,13:17)=-100;
environment(7,14:18)=-100;
environment(3:10,19)=-100;
environment(15:18,19)=-100;
environment(3:10,19)=-100;
environment(3:10,7)=-100;
environment(9:19,2)=-100;
environment(15:17,7)=-100;
environment(10,3:7)=-100;
environment(13,5:8)=-100;
environment(6:8,4)=-100;
environment(13:18,4)=-100;
environment(6:16,10)=-100;
environment(19:20,10)=-100;
environment(17,13:17)=-100;
environment(18,6:11)=-100;
environment(10:17,13)=-100;
environment(10,13:17)=-100;
environment(14,15:19)=-100;
nvironment(7,12)=-100;
% 展示生成的环境地图矩阵
disp('Environment matrix is: (1 represents valid path,-100 represents unvalid path, 0 represents start or goal)')
disp(environment)
% 展示可视化的环境地图
figure(1);
% imagesc()函数将矩阵environment中的元素数值按大小转化为不同颜色
imagesc(environment)
axis equal
% 指定机器人运动的起点和终点的x,y值,对应的起点和终点在矩阵中分别标为1和10
% 自动初始化确定起点和终点的x,y坐标
Start_point_x = 2;
Start_point_y = 6;
End_point_x = 18;
End_point_y = 19;
% 也可由用户手动输入起点和终点的x,y坐标(取消下面注释即可)
% while 1
% Start_point_x = input('起点x坐标:');
% Start_point_y = input('起点y坐标:');
% End_point_x = input('终点x坐标:');
% End_point_y = input('终点y坐标:');
% if environment(Start_point_x ,Start_point_y) ~= -100 && environment(End_point_x,End_point_y) ~= -100
% break;
% end
% fprintf("起点或终点不能使用,请重新输入\n");
% end
environment(Start_point_x ,Start_point_y ) = 20; % 指定起点坐标
environment(End_point_x,End_point_y) = 20; % 指定终点坐标
disp(environment)
imagesc(environment)
% 起点标为SP,终点标为EP
text(Start_point_y ,Start_point_x ,'SP','HorizontalAlignment','center')
text(End_point_y,End_point_x,'EP','HorizontalAlignment','center')
title('机器人运动环境地图');
axis equal
axis off
environment(Start_point_x ,Start_point_y ) = 1;
% 输出environment矩阵大小
Size = n*n;
fprintf('Size of environment matrix is: %d\n',Size)
%% 构造奖励矩阵reward
% 有八种可能的运动状态,如下:
% * 向上运动 : (i-n);% * 向下运动 : (i+n)
% * 向左运动 : (i-1);% * 向右运动 : (i+1)
% * 向右下运动 : (i+n+1);% * 向左下运动 : (i+n-1)
% * 向右上运动 : (i-n+1);% * 向左上运动 : (i-n-1)
% reward矩阵初始化为0
reward=zeros(Size);
for i=1:Size
reward(i,:) = reshape(environment',1,Size); % 矩阵environment的元素返回到一个Size×Size的矩阵reward
end
%将斜向运动的奖励矩阵值赋为0.7071
for i=1:Size
for j=1:Size
if(i+n+1<400 && reward(i,i+n+1)~=-100)
reward(i,i+n+1) = 1/sqrt(2);
end
if(i+n-1>0 && i+n-1<400 && reward(i,i+n-1)~=-100)
reward(i,i+n-1) = 1/sqrt(2);
end
if(i-n+1>0 && i-n+1<400 &&reward(i,i-n+1)~=-100)
reward(i,i-n+1) = 1/sqrt(2);
end
if(i-n-1>0 && reward(i,i-n-1)~=-100)
reward(i,i-n-1) = 1/sqrt(2);
end
end
end
for i=1:Size
for j=1:Size
if j~=i-n && j~=i+n && j~=i-1 && j~=i+1 && j~=i+n+1 && j~=i+n-1 && j~=i-n+1 && j~=i-n-1
reward(i,j) = -Inf;
end
end
end
for i=1:n:Size
for j=1:i+n
if j==i+n-1 || j==i-1 || j==i-n-1
reward(i,j) = -Inf;
reward(j,i) = -Inf;
end
end
end
%% 通过循环迭代得到Q-learning算法的Q值表
% 设置Q-learning算法参数的gamma,alpha,循环迭代次数number和终点Goal
q = 0.5*ones(size(reward)); % 产生标准正态分布的n*n随机数矩阵
gamma = 0.9;
alpha = 0.6;
number = 80;
Goal = (End_point_x - 1)*n + End_point_y;
Min_number_of_total_steps = 400;
len = zeros(1,number); %存储每次迭代路径长度
% 循环迭代
% initial:当前状态
% next: 下个状态
for i=1:number
% 开始状态
initial = 1;
% 重复运行,直至到达goal状态
while(1)
% 选择状态的所有可能行动 n_actions,n_actions是一个行向量
next_actions = find(reward(initial,:)>0); % find()函数的基本功能是返回向量或者矩阵中不为0的元素的位置索引
% 随机选择一个动作,并把它作为下一状态
next = next_actions(randi([1 length(next_actions)],1,1)); % randi()函数生成从1-length(n_actions)均匀分布的伪随机整数
% 找到所有可能的动作
next_actions = find(reward(next,:)>=0);
% 找到最大的Q值,也就是说,为下一个行动最好的状态
max_q = 0;
for j=1:length(next_actions)
max_q = max(max_q,q(next,next_actions(j)));
end
% 利用Bellman's equation更新Q值表
q(initial,next) = (1-alpha)*q(initial,next) + alpha*(reward(initial,next) + gamma*max_q);
% 检查是否到达终点
if(initial == Goal)
break;
end
% 把下一状态设置为当前状态
initial = next;
end
if i<=80
%% 下面使用Q-learning算法来进行路径规划
start = (Start_point_x-1)*n + Start_point_y;
path = start;
move = 0;
% 循环迭代直至找到终点Goal
while(move~=Goal)
% 从起点开始搜索
[~,move] = max(q(start,:));
% sort()排序函数,按降序排序
% 消除陷入小循环的情况
step = 2;
while ismember(move,path)
[~,x] = sort(q(start,:),'descend');
move = x(step);
step = step + 1;
end
% 加上下一个动作到路径中
path = [path,move];
start = move;
end
%% 输出当前机器人的最短路径和最短路径步数
if length(path) < Min_number_of_total_steps
Min_number_of_total_steps = length(path);
end
%fprintf('Final path is: %s\n',num2str(path)) % num2str()函数把数值转换成字符串,转换后使用fprintf函数进行输出
for k=2:length(path)
if abs(path(k)-path(k-1))==1 || abs(path(k)-path(k-1))==20
len(i) = len(i) +1;
else
len(i) = len(i) + 1.4;
end
end
fprintf('%d Number of total steps is : %.1f\n',i,len(i))
% 将路径加入到新的路径矩阵pmat中
pmat = zeros(n,n);
[Q, r] = quorem(sym(path),sym(n));
Q = double(Q);
r = double(r);
Q(r~=0) = Q(r~=0) + 1;
r(r==0) = n;
for j = 1:length(Q)
pmat(Q(j),r(j)) = 50;
end
%% 绘制机器人寻找最短路径的过程
figure(2);
if mod(i,8)==0 && i<72
subplot(3,3,fix(i/8));
end
imagesc(pmat)
for x=1:n
for j=1:n
if pmat(x,j)==50
text(j,x,'\bullet','Color','red','FontSize',20)
end
end
end
text(Start_point_y ,Start_point_x ,'SP','HorizontalAlignment','center')
text(End_point_y,End_point_x,'EP','HorizontalAlignment','center')
hold on
imagesc(environment,'Alphadata',0.5)
colormap(spring)
axis equal
hold off
if mod(i,8)==0
title(i);
end
axis off
end
end
%% 绘制机器人最终的最短路径
figure(3)
imagesc(pmat)
for x=1:n
for j=1:n
if pmat(x,j)==50
text(j,x,'\bullet','Color','red','FontSize',20)
end
end
end
text(Start_point_y ,Start_point_x ,'SP','HorizontalAlignment','center')
text(End_point_y,End_point_x,'EP','HorizontalAlignment','center')
hold on
imagesc(environment,'Alphadata',0.5)
colormap(spring)
axis equal
hold off
title('机器人最终的最短路径可视化');
axis off
%% Q learning算法规划的路径长度变化趋势
figure(4);
plot(1:number,len,'-');
title('Q learning算法规划路径长度变化趋势');
hold on