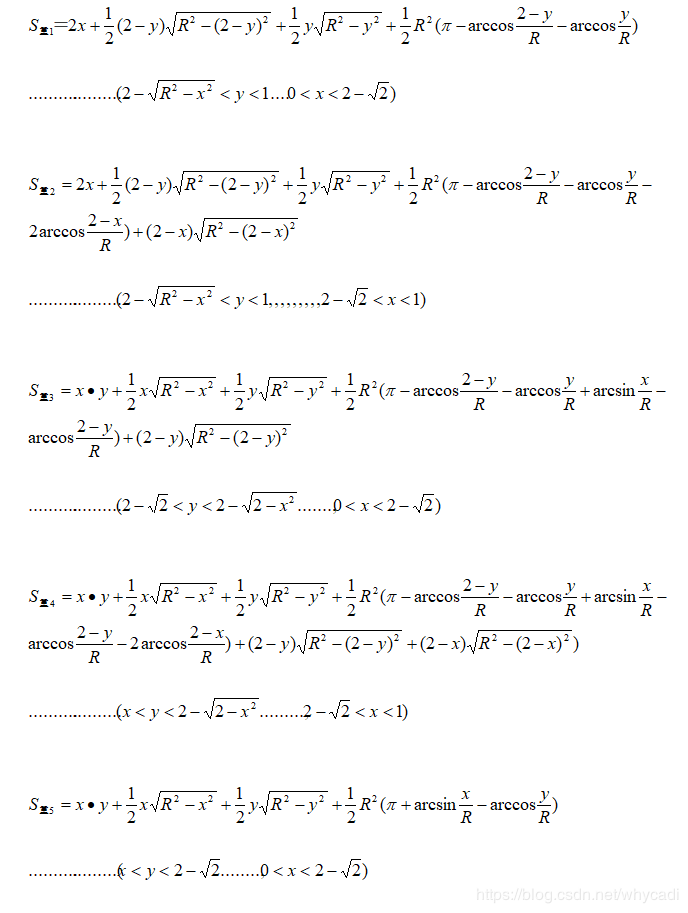一个2×2的正方形,每次在其中随机取两点,这两点的距离小于√2的概率是多少?
这是我很多年前第一篇在scdn上写的博客,只是当时不会贴贴图,所以图都没有,是个不完整的博客。今天突然想起还一直留着这个问题没填,所以重新把图贴上了。了个事。
题目:
一个2×2的正方形,每次在其中随机取两点,这两点的距离小于√2的概率是多少?
分析:
从题目看两个点正方形中的分布应是平均分布。第一个点落入正方形中任意点的概率是F1=1/S正,第二个点与第一个点是独立的,它落入正方形任意点的概率同第一点,既F2=1/S正。 第二点与第一点距离小于√2的概率F1,2=以第一点为圆心,√2为半径的圆与正方形重合的部分的面积S重/S正。
总的概率为 F=∫∫F1×F1,2 S正。
解法:
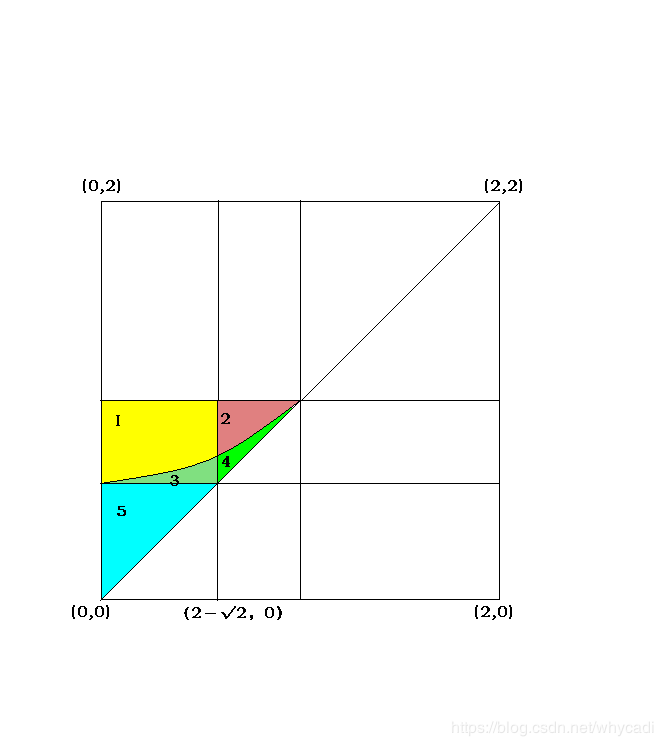
如图将正方形分成8个三角形,由于是全对称的,只考虑第一点落在彩色三角中的情况。
现在要求出以这个点为圆心,半径为√2的圆与正方形重合的面积。不过由于以不同的点为圆心画圆时,与正方形各边的覆盖情况不同,所以需要区分对待。
通过分析,可以将这个三角再如图划分为5个部分,每个区域内的S重具有相同的形式。圆心在区域1时,这个圆会盖住左边两个顶点,与上下两边相交,不予右边相交。而在区域2时,会覆盖左上、左下、两个顶点并与右边有两个交点,区域3则不能覆盖左上顶点,但与上边有两个交点,区域4则与上边和右边都有两个交点,区域5则与上边和右边都没有交点。
下面写出各部分S重n的表达式:
其中R=√2
以后的工作就是对以上各式在其积分域内积分。这个工作可以利用Matlab来完成。
用Matlab编写.M文件来完成以上工作,M文件如下:
clear all;
r=sqrt(2);
sum=0;
%定义符号变量
syms x y;
%定义各部分面积计算式
s(1)=2*x+1/2*(2-y)*sqrt(2-(2-y)^2)+1/2*y*sqrt(2-y^2)+pi-acos((2-y)/r)-acos(y/r);
s(2)=2*x+1/2*(2-y)*sqrt(2-(2-y)^2)+1/2*y*sqrt(2-y^2)+pi-acos((2-y)/r)-acos(y/r)-2*acos((2-x)/r)+(2-x)*sqrt(2-(2-x)^2);
s(3)=x*y+1/2*x*sqrt(2-x^2)+1/2*y*sqrt(2-y^2)+pi-acos((2-y)/r)-acos(y/r)+asin(x/r)-acos((2-y)/r)+(2-y)*sqrt(2-(2-y)^2);
s(4)=x*y+1/2*x*sqrt(2-x^2)+1/2*y*sqrt(2-y^2)+pi-acos((2-y)/r)-acos(y/r)+asin(x/r)-acos((2-y)/r)-2*acos((2-x)/r) ...
+(2-y)*sqrt(2-(2-y)^2)+(2-x)*sqrt(2-(2-x)^2);
s(5)=x*y+1/2*x*sqrt(2-x^2)+1/2*y*sqrt(2-y^2)+pi+asin(x/r)-acos(y/r);
%定义各部分积分域
area_y=[2-sqrt(2-x^2),1;
2-sqrt(2-x^2),1;
2-r,2-sqrt(2-x^2);
x,2-sqrt(2-x^2);
x,2-r];
area_x=[0,2-r;
2-r,1;
0,2-r;
2-r,1;
0,2-r];
%计算积分
for n=1:5
temp(n)=int(s(n),y);
fx(n)=subs(temp(n),y,area_y(n,2))-subs(temp(n),y,area_y(n,1));
end
for n=1:5
temp(n)=int(fx(n),x);
f(n)=subs(temp(n),x,area_x(n,2))-subs(temp(n),x,area_x(n,1));
sum=sum+f(n);
end
然而很不幸的是,运行时提示有误,经检查发现是第二轮积分有式子得不到解析解,所以必须另想办法。
经过分析,我发现第一轮积分后,将y值按各积分域的值代入,使式子复杂化,所以产生了无法得到解析解的情况,但是实际上有些因子比如1/2× y√(2-y^2)在不止一个区域里出现,而将几个相邻的积分域合并的话,可以简化积分后的结果。
将所有出现的因子和出现的域列表
|
|
1 |
2 |
3 |
4 |
5 |
| 2x |
Y |
Y |
|
|
|
| 1/2*(2-y)*sqrt(2-(2-y)^2) |
Y |
Y |
|
|
|
| 1/2*y*sqrt(2-y^2) |
Y |
Y |
Y |
Y |
Y |
| pi |
Y |
Y |
Y |
Y |
Y |
| -acos(y/r) |
Y |
Y |
Y |
Y |
Y |
| -acos((2-y)/r) |
Y |
Y |
Y |
Y |
|
| -2*acos((2-x)/r) |
|
Y |
|
Y |
|
| (2-x)*sqrt(2-(2-x)^2) |
|
Y |
|
Y |
|
| x*y |
|
|
Y |
Y |
Y |
| 1/2*x*sqrt(2-x^2) |
|
|
Y |
Y |
Y |
| asin(x/r) |
|
|
Y |
Y |
Y |
| -acos((2-y)/r) |
|
|
Y |
Y |
|
| (2-y)*sqrt(2-(2-y)^2) |
|
|
Y |
Y |
|
|
|
积分结果 |
|
| 2x |
-5/3+4/3*2^(1/2) |
|
| 1/2*(2-y)*sqrt(2-(2-y)^2) |
1/8 |
|
| 1/2*y*sqrt(2-y^2) |
pi/16 |
|
| pi |
pi/2 |
|
| -acos(y/r) |
-1/4*pi+1/4 |
|
| -acos((2-y)/r) |
1/2*pi-7/4 |
|
| -2*acos((2-x)/r) |
-1/2*pi+3/2 |
|
| (2-x)*sqrt(2-(2-x)^2) |
-1/3+1/8*pi |
|
| x*y |
23/12-4/3*2^(1/2) |
|
| 1/2*x*sqrt(2-x^2) |
-17/24-1/16*pi+2/3*2^(1/2) |
|
| asin(x/r) |
0.04124498 |
得不到解析解 |
| -acos((2-y)/r) |
-0.01347756 |
得不到解析解 |
| (2-y)*sqrt(2-(2-y)^2) |
5/12-1/8*pi |
|
| 和= |
1.50597463 |
|
| 总概率=和/2= |
0.75298731 |
|
| 精确值 |
2/3√2+pi/4-1/4+∫∫…dΩ |
|
为便于计算,写了两个M文件来进行积分,这两个文件分别是先积x方向和先积y方向。程序如下:
file name intxy:
fxy=int(f,x);
f1=subs(fxy,x,area_xy(2))-subs(fxy,x,area_xy(1));
f2=simple(f1);
fs=int(f2,y,area_xy(3),area_xy(4));
file name intyx:
fxy=int(f,y);
f1=subs(fxy,y,area_yx(2))-subs(fxy,y,area_yx(1));
f2=simple(f1);
fs=int(f2,x,area_yx(3),area_yx(4));
在实践过程中,发现有时在积分前用 simple 函数对被积函数化简是很重要的,否则会得不到正确解。
对于两个不能得到解析解的因子,只好采用数值积分的方法得到近似解了。所用的函数是trapz(x,y)。x是取值在积分域上的一个向量,所取得间隔是0.0001,y是因子注变量取x时得到的值向量。
也可以用quad(@fx,a,b)指令,fx是一个函数M文件。两个函数文件分别是:
function y=fx(x)
y=(sqrt(2-(2-x).^2)-x).*acos((2-x)./sqrt(2));
function y=fx1(x)
y=(2-(2-x.^2).^(1/2)-x).*asin(x./sqrt(2));
注:这个因子是已经对一个变量积分一次,将该变量积分域代入后得到一个一元函数。
通过模拟,证实了以上结果的正确。模拟程序是随机取了1G对(2^30)的点进行统计,得到的结果非常吻合。模拟程序如下:
clear all;
sum=[0,0];
tic
for n=1:1024
a=rand(2,1024*1024);
b=rand(2,1024*1024);
a=b-a;
b=a(1,:).*a(1,:)+a(2,:).*a(2,:);
bound=[0,1];
y=hist(b,bound);
sum=sum+y;
end
prob=sum./2^30
t=toc
2003-8-8 补充
今天使用Mathematica5.0软件计算用Matlab无法计算出的两个积分,发现可以算出。
约等于0.7529872852