分类器的不同的性能评价指标

参考链接：精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？

读取混淆矩阵（confusion matrix）

混淆矩阵是一个2×2的方阵，用于展示分类器预测的结果——真正（true positive），假负（false negative）、假正（false positive）及假负（false negative）

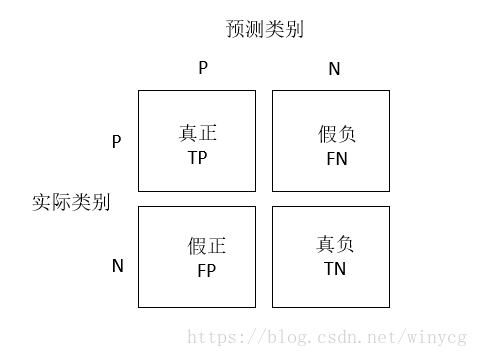
sklearn中使用confusion_matrix函数实现：

import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix
from sklearn.pipeline import Pipeline
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split

'''
读取乳腺癌数据集
数据集前两列存储样本ID和诊断结果（M代表恶性，B代表良性）
3~32列包含了30个特征
'''
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases'
                 + '/breast-cancer-wisconsin/wdbc.data',
                 header=None)
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le =LabelEncoder()
# 将类标从字符串(M或B)变为整数的(0,1)
y = le.fit_transform(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

'''
在流水线中集成标准化操作以及分类器
PipeLine对象采用元组的序列作为输入，每个元组第一个值为字符串，
可以通过字符串访问流水线的元素，第二个值为sklearn中的转换器或评估器
'''
pipe_svc = Pipeline([
    ('scl', StandardScaler()),
    ('clf', SVC(random_state=0))
])

pipe_svc.fit(X_train, y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)
'''
[[67 0
  2  45]]
'''
fig, ax = plt.subplots(figsize=(2.5, 2.5))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
# 给图形上文字，表示各情况的样本数量
for i in range(confmat.shape[0]):
    for j in range(confmat.shape[1]):
        ax.text(x=j, y=i, s=confmat[i, j], va='center', ha='center')
plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show()

从下图可以看出，模型正确预测出了类别为0的样本数量是67，还有45个属于类别1的样本。

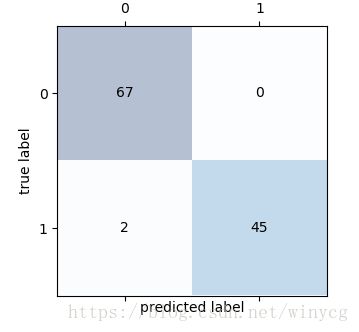
精确率，召回率和P-R曲线

错误率（error，ERR）为预测错误的样本的数量与所有被预测样本数量的比值，而准确率（accuracy，ACC）为预测正确的样本的数量与所有被预测样本数量的比值。

ERR=FP+ENFP+FN+TP+TN E R R = F P + E N F P + F N + T P + T N

ACC=TP+TNFP+FN+TP+TN=1−ERR A C C = T P + T N F P + F N + T P + T N = 1 − E R R

查准率（precision，PRE）针对预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。

P=TPTP+FP P = T P T P + F P

查全率（recall，REC）针对样本而言的，它表示的是正样本中有多少被预测正确

R=TPTP+FN R = T P T P + F N

P-R曲线：假设一共有20个测试样本，根据每个测试样本属于正样本的概率值从小到大排序。接下来，从高到低依次将概率值”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。由此可以得到20组precision和recall值，进而可以画出P-R曲线。
P-R曲线查准率=查全率的点称为平衡点（Break-Even Point，BEP），平衡点的值作为分类器性能的度量。

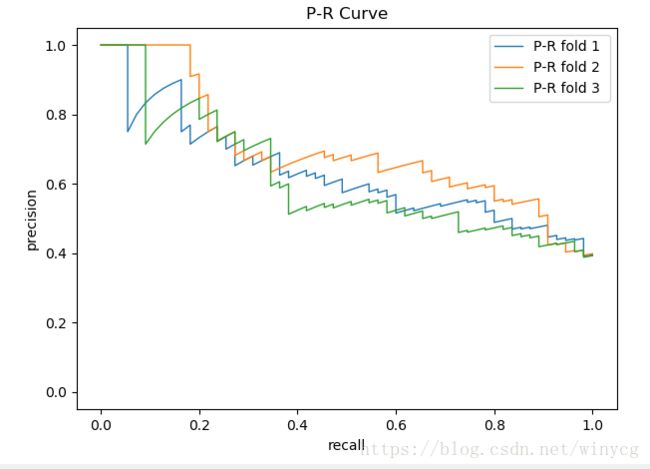
BEP过于简化，常用的F1度量
F1分数是精确率和召回率的调和平均数：

F1=21P+1REC=2(P×R)P+R F 1 = 2 1 P + 1 R E C = 2 ( P × R ) P + R

在算数平均数中，重要性取决于绝对值大的一方；调和平均数中，重要性取决于绝对值小的一方。
F1度量的一般形式为 Fβ F β ,可以表现出查准率和查全率的不同重要程度。

Fβ=(1+β2)×P×R(β2×P)×R F β = ( 1 + β 2 ) × P × R ( β 2 × P ) × R

当 β=1 β = 1 时，为标准的F1度量。当 β>1 β > 1 时，查全率有更大影响；当 β<1 β < 1 时，查准率有更大影响

from sklearn.metrics import precision_score, recall_score, 
f1_score, fbeta_score
print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))
print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))
print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))
print('F_beta: %.3f' % fbeta_score(y_true=y_test, y_pred=y_pred, beta=0.8))
'''
Precision: 1.000
Recall: 0.957
F1: 0.978
F_beta: 0.983
'''

ROC曲线

对于类别数量不均衡的分类问题来说，真正率（TPR）和假正率（EPR）非常有用：

TRP=TPP=TPFN+TP T R P = T P P = T P F N + T P

FRP=FPN=FPFP+TN F R P = F P N = F P F P + T N

受试者工作特征曲线（Receiver Operator Characteristic，ROC）是基于模型假正率和真正率等性能指标进行分类模型选择的工具。
参考链接： http://alexkong.net/2013/06/introduction-to-auc-and-roc/
假设一共有20个测试样本，根据每个测试样本属于正样本的概率值从大到小排序。接下来，从高到低依次将概率值”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。由此可以得到20组FPR和TPR值，进而可以画出ROC曲线。
AUC(Area Under the Curve)为ROC曲线下方区域的面积，面积的数值在1之内，一般都在0.5~1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。完美性能的AUC为1，随机选择的AUC为0.5。

import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split

'''
读取乳腺癌数据集
数据集前两列存储样本ID和诊断结果（M代表恶性，B代表良性）
3~32列包含了30个特征
'''
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases'
                 + '/breast-cancer-wisconsin/wdbc.data',
                 header=None)
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le =LabelEncoder()
# 将类标从字符串(M或B)变为整数的(0,1)
y = le.fit_transform(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

pipe_lr = Pipeline([
    ('scl', StandardScaler()),
    ('clf', LogisticRegression(penalty='l2', random_state=0))
])

from sklearn.metrics import roc_curve, auc
from scipy import interp
from sklearn.model_selection import StratifiedKFold


X_train2 = X_train[:, [4, 14]]
skf = StratifiedKFold(n_splits=3, random_state=0)
cv = skf.split(X_train2, y_train)
mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []

fig = plt.figure(figsize=(7, 5))
for i, (train, test) in enumerate(cv):
    probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])
    # 根据概率获得fpr,tpr和阈值数据,pos_label指定了1作为正类别
    fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)
    print(thresholds)
    # 线性插值获得数据
    mean_tpr += interp(mean_fpr, fpr, tpr)
    mean_tpr[0] = 0.0
    plt.plot(fpr, tpr, lw=1, label='ROC fold %d (area=%.2f)' % (i+1, auc(fpr, tpr)))

# 随机猜测ROC曲线
plt.plot([0, 1], [0, 1], linestyle='--', color=(0.6, 0.6, 0.6), label='random guessing')

mean_tpr /= i+1
mean_tpr[-1] = 1.0
plt.plot(mean_fpr, mean_tpr, 'k--', lw=2,
         label='mean ROC (area=%.2f)' % (auc(mean_fpr, mean_tpr)))
# 完美性能ROC曲线
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', c='k', label='Perfect Performance')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Ratio')
plt.ylabel('True Positive Ratio')
plt.title('Receiver Operator Characteristic')
plt.legend(loc='lower right')
plt.show()

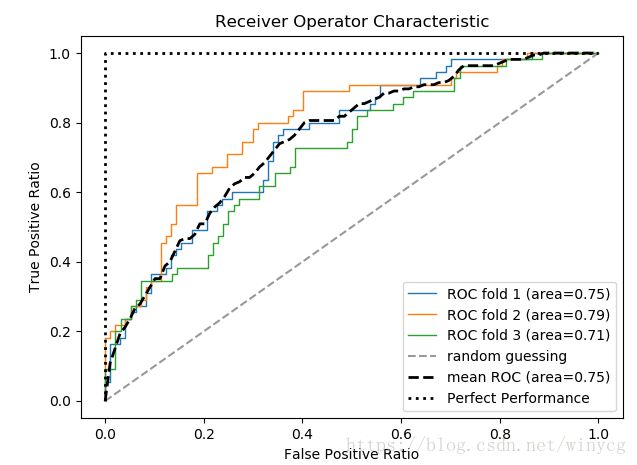
如果仅获取ROC AUC的分数，可以直接使用sklearn.metrics模块中导入roc_auc_score函数，计算分类器在测试集上的ROC AUC得分：

from sklearn.metrics import roc_auc_score
from sklearn.metrics import accuracy_score
print(roc_auc_score(y_true=y_test, y_score=y_pred))
print(accuracy_score(y_true=y_test, y_pred=y_pred))

在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），此时precision-Recall曲线会变化很大，ROC曲线基本不变。
原因是：假设数据集中只有100个positive instances,却有15200个negative instances，这属于极不均匀的数据集。假设分类器将1600 (1520+80)个instance分为positive,而其中实际上只有80个是真正的positive。 凭直觉来看，其实这个分类器并不好。但由于真证negative instances的数量远远大约positive, ROC的结果却很好，而PRC的precision可以判断出分类器性能较差。

多类别分类的评价标准

将二类别的评价标准通过一对多(One vs All,OvA)扩展到多分类问题。在k类别分类矩阵中，会有k个混淆矩阵。

微均值

将混淆矩阵对应的TP和FP元素相加，具体过程为：

Pmicro=∑ki=1TPi∑ki=1TPi+∑ki=1FPi P m i c r o = ∑ i = 1 k T P i ∑ i = 1 k T P i + ∑ i = 1 k F P i

Rmicro=∑ki=1TPi∑ki=1TPi+∑ki=1FNi R m i c r o = ∑ i = 1 k T P i ∑ i = 1 k T P i + ∑ i = 1 k F N i

Fmicro=2(Pmicro×Rmicro)Pmicro+Rmicro F m i c r o = 2 ( P m i c r o × R m i c r o ) P m i c r o + R m i c r o

宏均值

在各混淆矩阵分别求的查准率和查重率，再计算平均值。

Pmacro=1k∑i=1kPi P m a c r o = 1 k ∑ i = 1 k P i

Rmacro=1k∑i=1kRi R m a c r o = 1 k ∑ i = 1 k R i

Fmacro=2(Pmacro×Rmacro)Pmacro+Rmacro F m a c r o = 2 ( P m a c r o × R m a c r o ) P m a c r o + R m a c r o

当等同看待每个实例或者每次预测时，采用微均值‘；宏均值适用于类标样本不平衡的情况下，使用加权宏均值，各类别以类内实例的数量作为评分的权值。sklearn中将加权宏均值作为多类别问题的默认值，如果需要采用微均值，可以采用make_scorer函数创建一个计分器：

from sklearn.metrics import make_scorer
pre_scorer = make_scorer(score_func=precision_score,
                         pos_label=1,
                         average='micro')